Atomové Orbitaly
orbital je kvantově mechanické upřesnění Bohrova orbitu. Na rozdíl od jeho konceptu jednoduché kruhové oběžné dráhy s pevným poloměrem jsou orbitaly matematicky odvozené oblasti vesmíru s různými pravděpodobnostmi, že mají elektron.
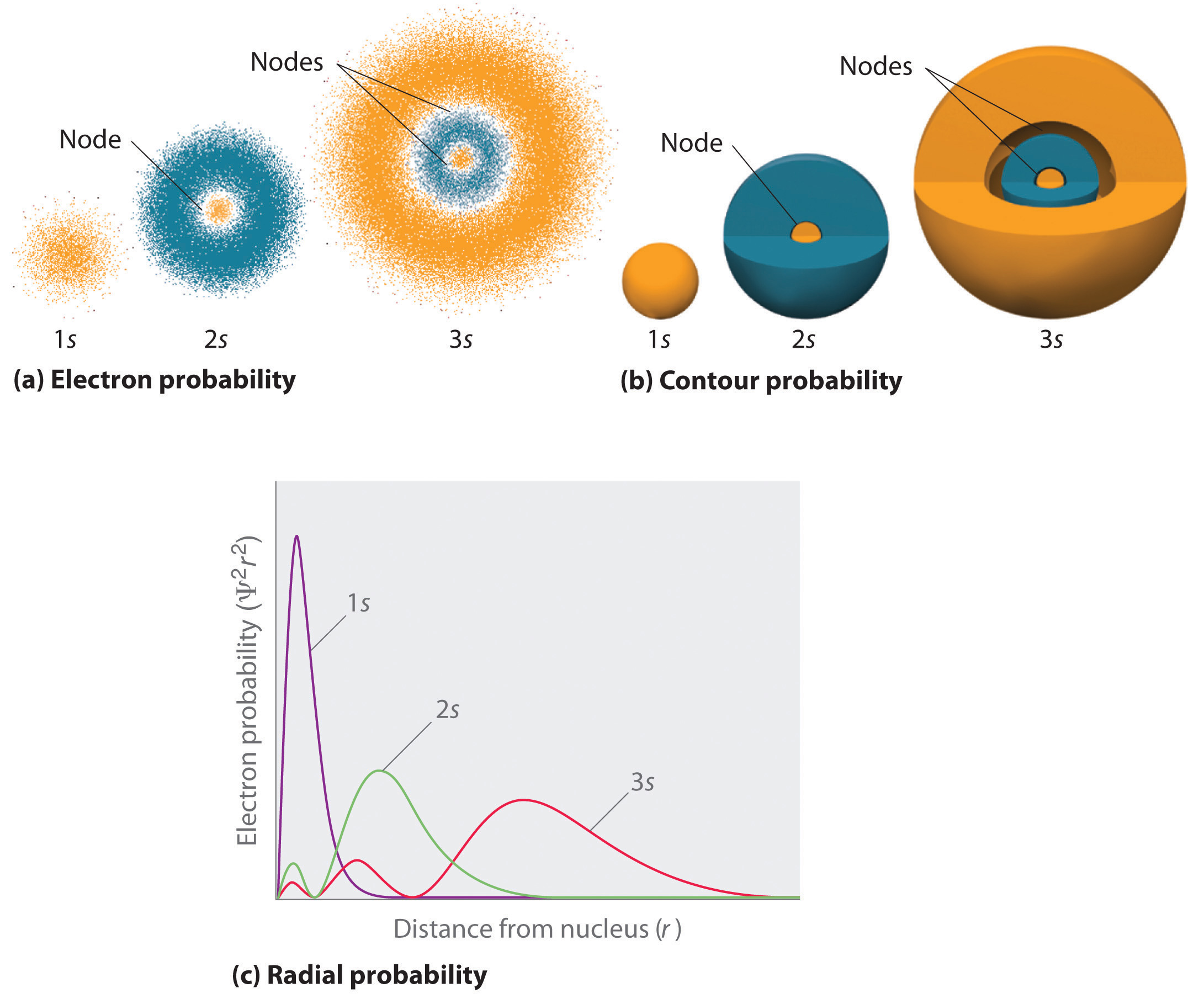
jeden způsob reprezentace distribuce pravděpodobnosti elektronů byl znázorněn na obrázku 6.5.2 pro 1s orbital vodíku. Protože Ψ2 dává pravděpodobnost nalezení elektronu v daném objemu prostoru (například krychlových picometer), pozemku Ψ2 versus vzdálenost od jádra (r) je graf hustoty pravděpodobnosti. 1s orbital je sféricky symetrické, takže pravděpodobnost nalezení 1s elektronů v daném bodě závisí pouze na jeho vzdálenosti od jádra. Hustota pravděpodobnosti je největší při r = 0 (v jádru) a neustále klesá s rostoucí vzdáleností. Při velmi velkých hodnotách r je hustota pravděpodobnosti elektronů velmi malá, ale ne nulová.
V kontrastu, můžeme vypočítat radiální pravděpodobnost (pravděpodobnost nalezení 1s elektron ve vzdálenosti r od jádra) sečtením pravděpodobností elektron je ve všech bodech na sérii x kulové skořepiny o poloměru r1, r2, r3,…, rx − 1, rx. V podstatě jsme rozdělení atomu na velmi tenké soustředné skořápky, stejně jako vrstvy cibule (část (a) na Obrázku \(\PageIndex{1}\)), a výpočet pravděpodobnosti nalezení elektronu na každé kulové skořepiny. Připomeňme si, že elektronové hustoty pravděpodobnosti je největší v r = 0 (část (b) na Obrázku \(\PageIndex{1}\)), takže hustota bodů je nejlepší pro nejmenší kulovité skořápky v části (a) na Obrázku \(\PageIndex{1}\). Naproti tomu povrchová plocha každé sférické skořápky je rovna 4nr2, což se velmi rychle zvyšuje se zvyšujícím se r (část (c) na obrázku \(\PageIndex{1}\)). Protože plocha kulové skořepiny zvyšuje rychleji s rostoucí r než elektronové hustoty pravděpodobnosti snižuje, děj radiální pravděpodobnost má maximum při určité vzdálenosti (část (d) na Obrázku \(\PageIndex{1}\)). Nejdůležitější, když r je velmi malý, ploše kulovitý shell je tak malý, že celková pravděpodobnost nalezení elektronu v blízkosti jádra je velmi nízká; na jádro, elektron, pravděpodobnost, že zmizí (část (d) na Obrázku \(\PageIndex{1}\)).

Pro atom vodíku, vrchol v radiálním pravděpodobnost, že děj nastává při r = 0.529 Å (52.9 pm), což je přesně to, poloměr vypočtený Bohr pro n = 1 oběžné dráze. Nejpravděpodobnější poloměr získaný z kvantové mechaniky je tedy totožný s poloměrem vypočítaným klasickou mechanikou. V Bohrově modelu se však předpokládalo, že elektron je v této vzdálenosti 100% času, zatímco v kvantově mechanickém Schrödingerově modelu je v této vzdálenosti jen část času. Rozdíl mezi těmito dvěma modely je způsoben vlnovitým chováním elektronu a heisenbergovým principem neurčitosti.
obrázek \(\PageIndex{2}\) porovnává hustoty pravděpodobnosti elektronů pro orbitaly vodíku 1s, 2s a 3s. Všimněte si, že všechny tři jsou sféricky symetrické. Pro 2s a 3s orbitalů, nicméně (a pro všechny ostatní s-orbitaly), elektronové hustoty pravděpodobnosti není spadnout plynule s rostoucí r. Místo toho, série minima a maxima jsou pozorovány v radiálním pravděpodobnost pozemků (část (c) na Obrázku \(\PageIndex{2}\)). Minima odpovídají kulovité uzly (regiony nulová pravděpodobnost, že elektron), které se střídají s kulovým regionech nenulová pravděpodobnost, že elektron.