Konigsberg este un oraș de pe râul Preger, care în secolul 18a fost un oraș German, dar acum este rus. În oraș sunt douăinsulele River care sunt conectate la maluri cu șapte poduri (așa cum se arată mai jos).

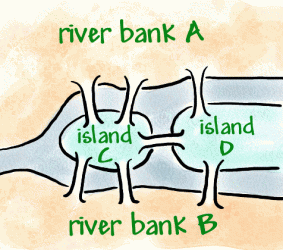
A devenit o tradiție să încerci să te plimbi prin oraș într-un mod care a traversat fiecare pod o singură dată, dar s-a dovedit a fi o problemă dificilă. Leonhard Euler, matematician elvețian în slujba luiîmpărăteasa Rusă Ecaterina cea mare, a auzit despre această problemă.În 1736 Euler a dovedit că plimbarea nu era posibilă. El a demonstrat acest lucru inventând un fel de diagramă numită rețea, care este alcătuită din vârfuri (puncte unde se întâlnesc liniile) și arce(linii).

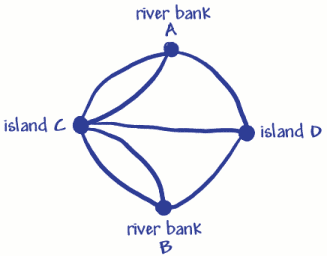
A folosit patru puncte (vârfuri) pentru cele două maluri ale râului și cele două insule. Acestea au fost marcate A, B și C, D. Cele șapte linii (arce) sunt cele șapte poduri. Puteți vedea că 3 poduri (arce)se alătură malului râului A și 3 se alătură malului râului B. 5 poduri (arce)se alătură insulei C și 3 se alătură insulei D. Aceasta înseamnă că toatevertexurile au un număr impar de arce, deci sunt numite oddvertexes. (Un vârf par ar trebui să aibă un număr par de arce care se alătură acestuia).
Amintiți-vă că problema a fost de a călători în jurul orașului de trecere fiecarepod doar o singură dată. În rețeaua lui Euler, aceasta însemna urmărirea fiecarearc o singură dată, vizitând toate vârfurile. Euler a dovedit că nu se poate face pentru că a realizat că pentru a avea un vârf ciudat trebuie să începi sau să închei călătoria la acel vârf. (Gândiți-vă la asta).Deoarece nu poate exista decât un început și un sfârșit, pot exista doar două noduri ciudate dacă veți putea urmări fiecare arc o singură dată. Deoarece problema podului are 4 noduri impare, nu este posibil să se facă! Ce se întâmplă dacă nu există noduri ciudate atoate? Poate fi urmărită această rețea?

invenția rețelelor a început un nou tip de geometrie numittopologie. Topologia este acum utilizată în mai multe moduri, inclusiv pentru planificareși cartografierea rețelelor feroviare. (Ahhh! Trenurile trebuiau să intrea….)