planul de coordonate
obiective de învățare
· Plot perechi ordonate pe un plan de coordonate.
· având în vedere o pereche ordonată, determinați cadranul acesteia.
Introducere
planul de coordonate a fost dezvoltat cu secole în urmă și rafinat de matematicianul francez Ren Descartes. În onoarea sa, sistemul este uneori numit Sistemul de coordonate carteziene. Planul de coordonate poate fi folosit pentru a trasa puncte și linii grafice. Acest sistem ne permite să descriem relațiile algebrice într-un sens vizual și, de asemenea, ne ajută să creăm și să interpretăm concepte algebrice.
Noțiuni de bază pentru a cunoaște planul de coordonate
probabil ați folosit un plan de coordonate înainte. De exemplu, ați folosit vreodată o suprapunere cu grilă pentru a cartografia poziția unui obiect? (Acest lucru se face adesea și cu hărți rutiere.)

această „hartă” folosește o grilă orizontală și verticală pentru a transmite informații despre locația unui obiect. Observați că Literele A-F sunt listate de-a lungul vârfului, iar numerele 1-6 sunt listate de-a lungul marginii din stânga. Locația generală a oricărui element de pe această hartă poate fi găsită utilizând litera și numărul pătratului grilei sale. De exemplu, puteți găsi elementul care există la pătrat „4F” mișcând degetul de-a lungul orizontalei la litera F și apoi drept în jos, astfel încât să fiți în linie cu 4. Veți găsi un disc albastru se află în această locație pe hartă.
planul de coordonate are elemente similare cu grila prezentată mai sus. Se compune dintr-o axă orizontală și o axă verticală, linii numerice care se intersectează în unghi drept. (Ele sunt perpendiculare între ele.)
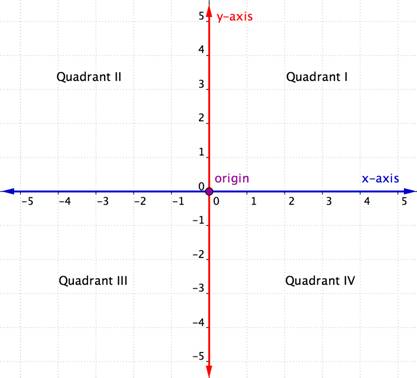
axa orizontală din planul de coordonate se numește axa X. Axa verticală se numește axa Y. Punctul în care se intersectează cele două axe se numește origine. Originea este la 0 pe axa x și 0 pe axa Y.axele X și y care se intersectează împart planul de coordonate în patru secțiuni. Aceste patru secțiuni sunt numite cadrane. Cadranele sunt denumite folosind cifrele romane I, II, III și IV începând cu cadranul din dreapta sus și deplasându-se în sens invers acelor de ceasornic.
locațiile de pe planul de coordonate sunt descrise ca perechi ordonate. O pereche ordonată vă spune locația unui punct raportând locația punctului de-a lungul axei x (prima valoare a perechii ordonate) și de-a lungul axei y (a doua valoare a perechii ordonate).
într-o pereche ordonată, cum ar fi (x, y), prima valoare se numește coordonata x, iar a doua valoare este coordonata Y. Rețineți că coordonata x este listată înainte de coordonata Y. Deoarece originea are o coordonată x de 0 și o coordonată y de 0, perechea sa ordonată este scrisă (0, 0).
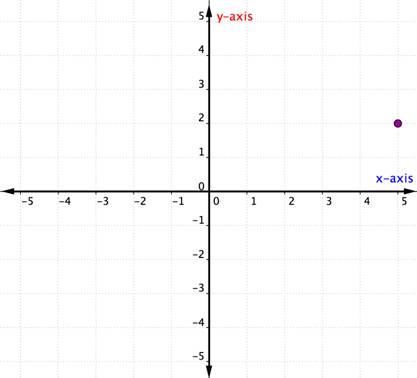
luați în considerare punctul de mai jos.
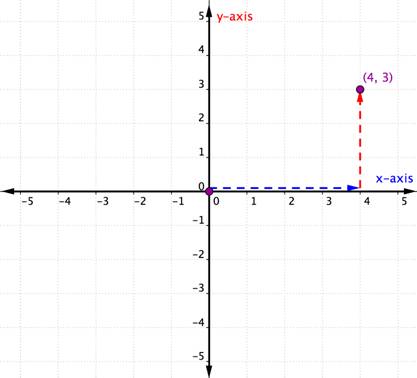
pentru a identifica locația acestui punct, începeți de la origine (0, 0) și deplasați-vă spre dreapta de-a lungul axei x până când vă aflați sub punct. Uită-te la eticheta de pe axa X. 4 indică faptul că, de la origine, ați călătorit patru unități spre dreapta de-a lungul axei X. Aceasta este coordonata x, primul număr din perechea ordonată.
de la 4 pe axa x deplasați-vă până la punct și observați numărul cu care se aliniază pe axa Y. 3 indică faptul că, după ce ați părăsit axa x, ați călătorit 3 unități în sus în direcția verticală, direcția axei Y. Acest număr este coordonata y, al doilea număr din perechea ordonată. Cu o coordonată x de 4 și o coordonată y de 3, aveți perechea ordonată (4, 3).
să ne uităm la un alt exemplu.
|
Example |
||
|
Problem |
Describe the point shown as an ordered pair. |
|
|
|
||
|
(5, y) |
începeți de la origine și deplasați-vă de-a lungul axei X. Aceasta este coordonata x și este scrisă mai întâi în perechea ordonată. |
|
|
(5, 2) |
treceți de la 5 până la perechea ordonată și citiți numărul de pe axa Y. Aceasta este coordonata y și este scrisă a doua în perechea ordonată. |
|
|
răspuns |
punctul prezentat ca o pereche ordonată este (5, 2). |
|
trasarea punctelor în planul de coordonate
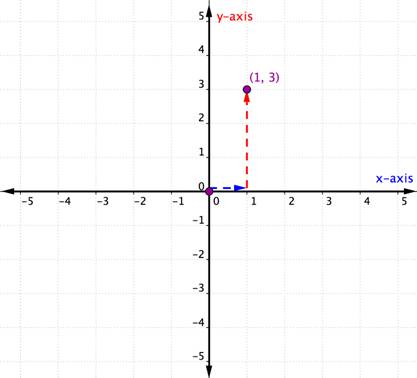
acum, că știți cum să utilizați axele X și Y, puteți trasa și o pereche ordonată. Amintiți—vă, ambele procese încep de la origine-începutul! Exemplul care urmează arată cum să graficați perechea ordonată (1, 3).
|
Example |
||
|
Problem |
Plot the point (1, 3). |
|
|
|
||
|
The x-coordinate is 1 because it comes first in the ordered pair. Începeți de la origine și deplasați o distanță de 1 unitate într-o direcție pozitivă (spre dreapta) de la origine de-a lungul axei X. |
coordonata y este 3 deoarece este a doua în perechea ordonată. De aici deplasați direct 3 unități într-o direcție pozitivă (în sus). Dacă te uiți la axa y, ar trebui să fii aliniat cu 3 pe acea axă. |
|
|
răspuns |
desenați un punct în această locație și etichetați punctul (1, 3). |
|
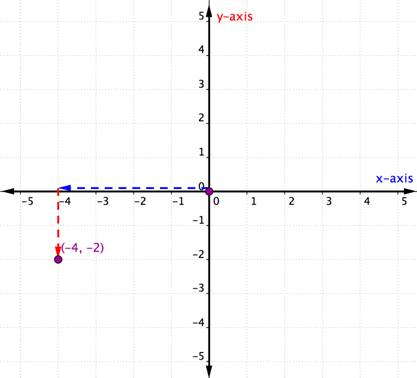
în exemplul anterior, atât coordonatele X, cât și Y au fost pozitive. Când una (sau ambele) dintre coordonatele unei perechi ordonate este negativă, va trebui să vă deplasați în direcția negativă de-a lungul uneia sau ambelor axe. Luați în considerare exemplul de mai jos în care ambele coordonate sunt negative.
|
Example |
||
|
Problem |
Plot the point (−4, −2). |
|
|
|
||
|
The x-coordinate is −4 because it comes first in the ordered pair. Începeți de la origine și mutați 4 unități într-o direcție negativă (stânga) de-a lungul axei X. |
coordonata y este -2 deoarece este a doua în perechea ordonată. Acum mutați 2 unități într-o direcție negativă (în jos). Dacă te uiți la axa y, ar trebui să fii aliniat cu -2 pe acea axă. |
|
|
răspuns |
desenați un punct în această locație și etichetați punctul (-4, -2). |
|
pașii pentru trasarea unui punct sunt rezumați mai jos.
pași pentru trasarea unei perechi ordonate (x, y) în planul de coordonate
o determinați coordonata X. Începând de la origine, deplasați orizontal, direcția axei x, Distanța dată de coordonata X. Dacă coordonata x este pozitivă, deplasați-vă spre dreapta; dacă coordonata x este negativă, deplasați-vă spre stânga.
o determinați coordonata Y. Începând de la coordonata x, deplasați-vă vertical, direcția axei y, distanța dată de coordonata Y. Dacă coordonata y este pozitivă, deplasați-vă în sus; dacă coordonata y este negativă, deplasați-vă în jos.
o desenați un punct la locația finală. Etichetați punctul cu perechea ordonată.
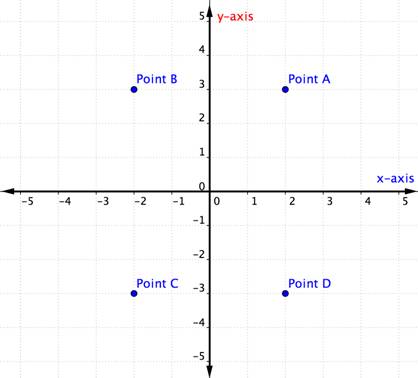
care punct reprezintă perechea ordonată (-2, -3)?
cele patru cadrane
perechi ordonate în cadrul unui anumit cadran împărtășesc anumite caracteristici. Uită-te la fiecare cadran din graficul de mai jos. Ce observați despre semnele coordonatelor x și y ale punctelor din fiecare cadran?
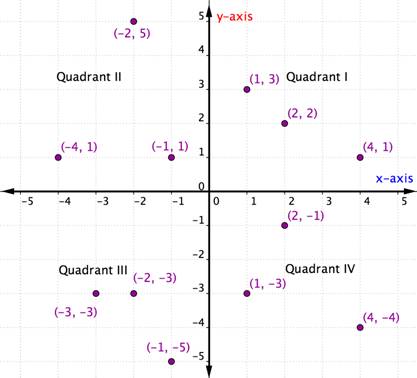
în fiecare cadran, semnele coordonatelor x și Y ale fiecărei perechi ordonate sunt aceleași. De asemenea, urmează un model, care este prezentat în tabelul de mai jos.
odată ce știți despre cadranele din planul de coordonate, puteți determina cadranul unei perechi ordonate fără să o graficați măcar uitându-vă la graficul de mai sus. Iată un alt mod de a gândi la asta.
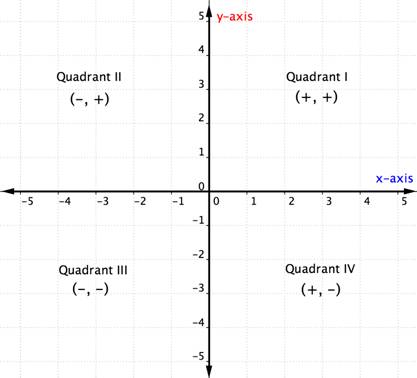
exemplul de mai jos detaliază cum se determină locația cadranului unui punct doar gândindu-se la semnele coordonatelor sale. Gândirea la locația cadranului înainte de a plota un punct vă poate ajuta să preveniți o greșeală. Este, de asemenea, cunoștințe utile pentru verificarea faptului că ați reprezentat corect un punct.
ce se întâmplă dacă o pereche ordonată are o coordonată X sau y de zero? Exemplul de mai jos prezintă graficul perechii ordonate (0, 4).
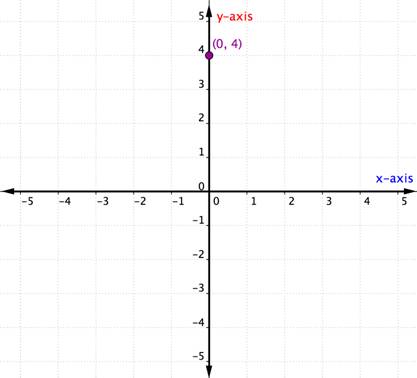
un punct situat pe una dintre axe nu este considerat a fi într-un cadran. Este pur și simplu pe una dintre axe. Ori de câte ori coordonata x este 0, punctul este situat pe axa Y. În mod similar, orice punct care are o coordonată y de 0 va fi localizat pe axa X.
care dintre descrierile de mai jos descrie cel mai bine locația punctului (8, 0)?
a) cadranul I
B) este pe axa x
C) este pe axa y
D) planul de coordonate
rezumat
planul de coordonate este un sistem de grafică și descriere a punctelor și liniilor. Planul de coordonate este format dintr-o axă orizontală (x -) și o axă verticală (y -). Intersecția acestor linii creează originea, care este punctul (0, 0). Planul de coordonate este împărțit în patru cadrane. Împreună, aceste caracteristici ale sistemului de coordonate permit reprezentarea grafică și comunicarea despre puncte, linii și alte concepte algebrice.