Algebra este foarte distractiv – veți obține pentru a rezolva puzzle-uri!
un Puzzle
care este numărul lipsă?
| − | 2 | = | 4 |
ok, răspunsul este 6, nu? Deoarece 6-2 = 4. Lucruri ușoare.
Ei bine, în algebră nu folosim cutii goale, folosim o literă (de obicei un x sau y, dar orice literă este în regulă). Așa că scriem:
| x | − | 2 | = | 4 |
este într-adevăr atât de simplu. Litera (în acest caz un x) înseamnă doar „nu știm încă acest lucru” și este adesea numită necunoscutul sau variabila.
și când o rezolvăm scriem:
| x | = | 6 |
Why Use a Letter?
| Because: | |
| it is easier to write „x” than drawing empty boxes (and easier to say „x” than „the empty box”). | |
| dacă există mai multe cutii goale (mai multe „necunoscute”) putem folosi o literă diferită pentru fiecare. |
deci x este pur și simplu mai bun decât să ai o cutie goală. Nu încercăm să facem cuvinte cu ea!
și nu trebuie să fie x, ar putea fi y sau w … sau orice literă sau simbol ne place.
Cum de a rezolva
Algebra este la fel ca un puzzle în cazul în care vom începe cu ceva de genul „x − 2 = 4” și vrem să se încheie cu ceva de genul „x = 6”.
dar în loc să spui „evident x=6”, folosește această abordare pas cu pas:
- află ce să elimini pentru a obține „x = …”
- scoateți-l făcând opusul (adăugarea este opusul scăderii)
- faceți asta ambelor părți
Iată un exemplu:
pentru a elimina
de „-2”
![]()
pentru a elimina, face
opusul, în acest caz se adaugă 2
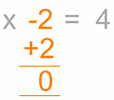
fă – o la
ambele părți
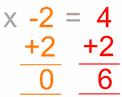
Care este …
![]()
rezolvat!
![]()
De ce am adăugat 2 la ambele părți?
pentru a „menține echilibrul”…
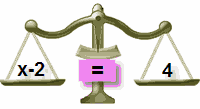
în echilibru
adăugați 2 la partea stângă

în afara echilibrului!
adăugați 2 și în partea dreaptă
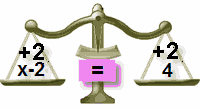
în echilibru din nou
amintiți-vă doar acest lucru:
pentru a menține echilibrul, ceea ce facem într-o parte a „=”
ar trebui să facem și în cealaltă parte!
See this in action at the Algebra Balance Animation.
Another Puzzle
Solve this one:
| x | + | 5 | = | 12 |
What we want is an answer like „x = …”,
but the +5 is in the way of that!
putem anula +5 cu un -5 (deoarece 5-5=0)
încercați-vă
acum exersați această foaie de lucru simplă de algebră și apoi verificați-vă răspunsurile. Încercați să utilizați pașii pe care vi i-am arătat aici, mai degrabă decât să ghiciți!
încercați întrebările de mai jos, apoi citiți Introducere în algebră-multiplicare