Purplemath
în matematică, o „identitate” este o ecuație care este întotdeauna adevărată. Acestea pot fi” Trivial „adevărate, cum ar fi” x = x „sau util adevărat, cum ar fi Teorema lui Pitagora” a2 + b2 = c2 ” pentru triunghiuri dreptunghiulare. Există o mulțime de identități trigonometrice, dar următoarele sunt cele pe care este cel mai probabil să le vedeți și să le utilizați.
Basic & Pythagorean, Angle-Sum & -Difference, Double-Angle, Half-Angle, Sum, Product
Content Continues Below
MathHelp.com
Need a custom math course?
K12 | College | Test Prep

identități de bază și pitagoreice
afiliat
observați cum un „co-(ceva)” raportul trig este întotdeauna reciproc al unui raport „non-co”. Puteți folosi acest fapt pentru a vă ajuta să păstrați drept că cosecant merge cu sine și secant merge cu cosinus.următoarele (în special prima dintre cele trei de mai jos) sunt numite identități „pitagoreice”.
sin2 (t) + cos2 ( t) = 1
tan2 (t) + 1 = sec2 (t)
1 + cot2 (t)=csc2(t)
publicitate
rețineți că cele trei identități implică mai presus de toate pătrat și numărul 1. Puteți vedea clar relația pitagoreică-Thereom dacă luați în considerare cercul unității, unde unghiul este t, partea „opusă” este sin(t) = y, partea „adiacentă” este cos(t) = x, iar hipotenuza este 1.
avem identități suplimentare legate de starea funcțională a raporturilor trig:
sin(–t) = –sin(t)
cos(–t) = cos(t)
tan(–t) = –tan(t)
observați în special că sinusul și tangenta sunt funcții impare, fiind simetrice în ceea ce privește originea, în timp ce cosinusul este o funcție uniformă, fiind simetric în ceea ce privește axis. Faptul că puteți lua semnul „minus” al argumentului în exterior (pentru sinus și tangent) sau îl puteți elimina în întregime (pentru cosinus) poate fi util atunci când lucrați cu expresii complicate.
Unghi de Sumă și Diferență Identități
sin(α + β) = sin(α) cos(β) + cos(α) sin(β)
sin(α – β) = sin(α) cos(β) – cos(α) sin(β)
cos(α + β) = cos(α) cos(β) – sin(α) sin(β)
cos(α – β) = cos(α) cos(β) + sin(α) sin(β)
apropo, în cele de mai sus identități, unghiurile sunt notate cu litere grecești. Litera de tip a, „XV”, se numește „alfa”, care se pronunță „AL-fuh”. Litera de tip B, „XV”, se numește „beta”, care se pronunță „BAY-tuh”.
conținutul continuă sub
identități cu unghi dublu
sin(2x) = 2 sin(x) cos(x)
cos(2x) = cos2(x)-sin2(x) = 1 – 2 sin2(x) = 2 cos2(x) – 1
identități cu jumătate de unghi
identitățile de mai sus pot fi re – enunțate prin pătrat fiecare parte și dublarea tuturor măsurilor de unghi. Rezultatele sunt următoarele:
Affiliate

Sum Identities
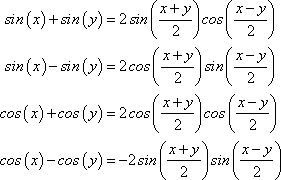
Product Identities
affiliate
veți folosi toate aceste identități, sau aproape așa, pentru a dovedi alte identități trig și pentru rezolvarea ecuațiilor trig. Cu toate acestea, dacă intenționați să studiați calculul, acordați o atenție deosebită identităților retratate sinus și cosinus semi-unghi, deoarece le veți folosi foarte mult în calculul integral.
URL: https://www.purplemath.com/modules/idents.htm