această secțiune acoperă:

• Introducere în funcții pe bucăți
• evaluarea funcțiilor pe bucăți
• grafice funcții pe bucăți
• cum să-i spuneți dacă o funcție pe bucăți este continuă sau non-continuă
• obținerea ecuațiilor din grafice funcționale pe bucăți
• valoare absolută ca funcție pe bucăți
• transformări ale funcțiilor pe bucăți
• probleme>

funcțiile în bucăți (sau funcțiile în bucăți) sunt exact ceea ce sunt numite: bucăți de funcții diferite (sub-funcții) toate pe un grafic. Cel mai simplu mod de a le gândi este dacă ați desenat mai multe funcții pe un grafic și ați șters doar părți ale funcțiilor în care nu ar trebui să fie (de-a lungul \(x\)’s); Ele sunt definite diferit pentru diferite intervale de \(x\). \(y\) este definit diferit pentru diferite valori ale \(x\); folosim \(x\) pentru a căuta în ce interval se află, astfel încât să putem afla ce ar trebui să fie \(y\).

rețineți că există un exemplu de inversare a unei funcții în bucăți aici în secțiunea inverse de funcții.

Here’s an example and graph:

Piecewise Function

Graph

\(\displaystyle f\left( x \right)=\left\{ \begin{align}2x+8\,\,\,\,\,&\text{ if }x\le -2\\{{x}^{2}}\,\,\,\,\,\,\,\text{ }\,&\text{ if }x>-2\end{align} \right.\) (există și alte modalități de a afișa acest lucru, cum ar fi utilizarea unui „pentru” în loc de un „dacă”, și folosind virgule sau semi-puncte în loc de „dacă”.) domeniu: \(\mathbb{R},\,\,\text{or}\,\, \ stânga ({- \infty, \ infty } \ dreapta)\) interval: \(\mathbb{R},\,\,\text{or}\,\,\stânga ({- \infty, \infty } \dreapta)\)

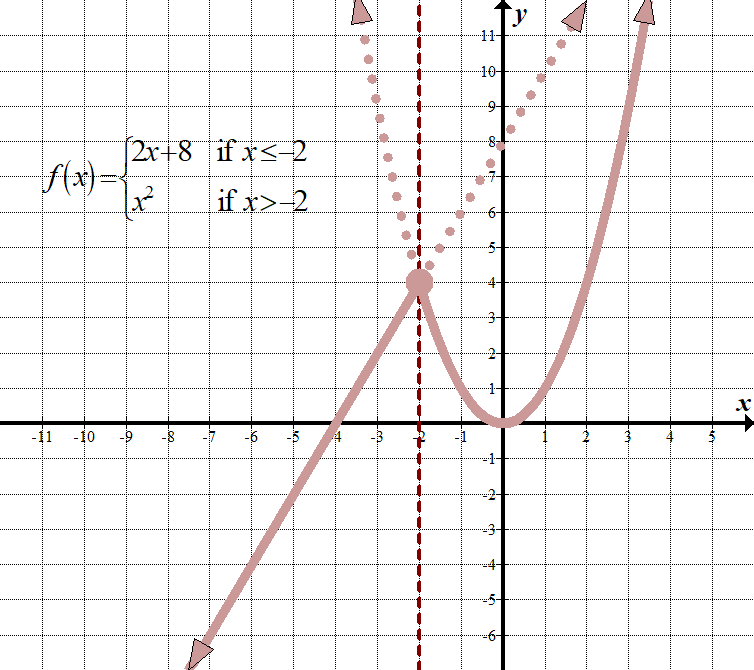ceea ce înseamnă acest lucru este pentru fiecare \(x\) mai mic sau egal cu -2, trebuie să graficăm linia \(2x+8\), ca și cum ar fi singura funcție din grafic. Pentru fiecare \(x\) valoare mai mare decât -2, trebuie să graficăm \({{x}^{2}}\), ca și cum ar fi singura funcție din grafic. Apoi trebuie să” scăpăm ” de părțile de care nu avem nevoie. Amintiți-vă că încă folosim originea ca punct de referință pentru ambele grafice!

vedeți cum linia verticală \(x=-2\) acționează ca o linie „limită” între cele două grafice?

rețineți că punctul \((-2,4)\) are un cerc închis pe el. Din punct de vedere tehnic, ar trebui să aparțină numai funcției \(2x+8\), deoarece această funcție are semnul mai mic sau egal, dar din moment ce punctul este și pe graficul \({{x}^{2}}\), putem folosi doar un cerc închis ca și cum ar apărea pe ambele funcții. Vezi, nu-i așa de rău, nu?

evaluarea funcțiilor pe bucăți

uneori, vi se vor oferi funcții pe bucăți și vi se va cere să le evaluați; cu alte cuvinte, găsiți valorile \(y\) atunci când vi se dă o valoare \(x\). Să facem acest lucru pentru \(x=-6\) și \(x=4\) (fără a utiliza graficul). Iată din nou funcția:

\(\displaystyle F\left( x \right)=\left\{ \begin{align}2x+8\,\,\,\,\,&\text{ dacă }x \ le -2 \ \ {{x}^{2}}\,\,\,\,\,\,\,\text { }\, &\text{ if }x>-2\end{align} \dreapta.\)

vrem mai întâi să ne uităm la condițiile din dreapta mai întâi, pentru a vedea unde este \(x\). Când \(x = -6\), știm că este mai mică de -2, așa că ne conectăm \(x\) la \(2x+8\) numai. \(f (x)\) sau\ (y\) este \((2)(-6)+8=-4\). Nici măcar nu ne pasă de\(\boldsymbol{{x}^{2}}\)! Este atât de ușor. De asemenea, puteți vedea că am făcut acest lucru corect folosind graficul de mai sus.

încercați acum \(x=4\). Ne uităm mai întâi la dreapta și vedem că \(x\) este mai mare decât -2, așa că îl conectăm în \({{x}^{2}}\). (Putem ignora doar \(2x + 8\) de data aceasta.) \(f (x)\) sau\ (y\) este \({{4}^{2}}=16\).

graficarea funcțiilor în bucăți

probabil vi se va cere să graficați funcțiile în bucăți. Uneori graficele vor conține funcții care nu sunt continue sau discontinue, ceea ce înseamnă că trebuie să vă ridicați creionul în mijlocul graficului atunci când îl desenați (ca un salt!). Funcțiile continue înseamnă că nu trebuie să vă ridicați niciodată creionul dacă ar fi să le desenați de la stânga la dreapta.

și amintiți-vă că graficele sunt funcții adevărate numai dacă trec testul de linie verticală.

să desenăm aceste funcții în bucăți și să determinăm dacă sunt continue sau non-continue. Rețineți cum desenăm fiecare funcție ca și cum ar fi singura, apoi „ștergem” părțile care nu sunt necesare. De asemenea, vom obține domeniul și gama așa cum am făcut aici în secțiunea funcții algebrice.

Piecewise Function	Graph
\(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}-2x+8\,\,\,\,\,\,\text{if }x\le 4\\\frac{1}{2}x-2\,\,\,\,\,\,\,\,\,\text{if }x>4\end{array} \right.\) Continuous Domain: \(\mathbb{R},\,\,\,\text{or}\,\,\left( {-\infty ,\infty } \right)\) Range: \(\left( {0,\infty } \right)\)
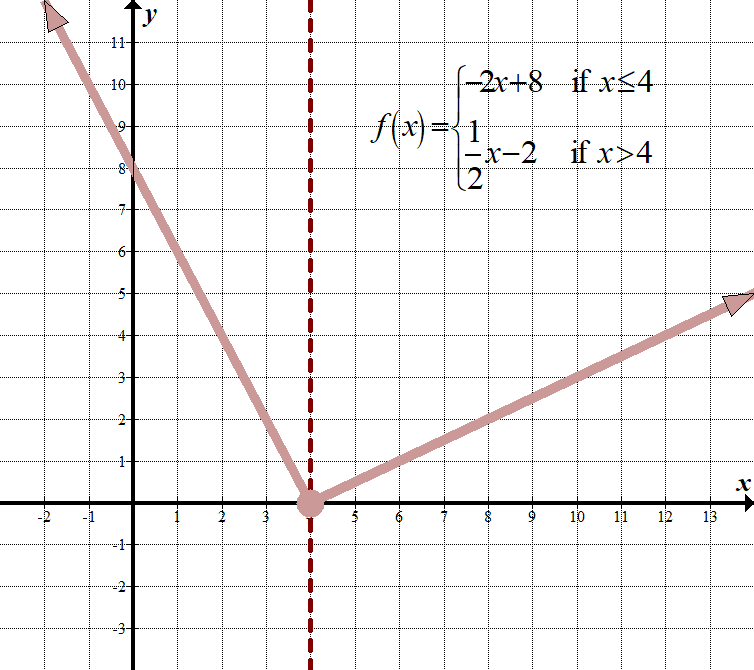\(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}x+4\,\,\,\,\,\,\,\,\,\text{if }x<1\\2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{if 1}\le x<4\\x-5\,\,\,\,\,\,\,\,\,\text{if }x\ge 4\end{array} \right.\) Non-Continuous Domain: \(\mathbb{R},\,\,\,\text{or}\,\,\left( {-\infty ,\infty } \right)\) Range: \(\mathbb{R},\,\,\,\text{or}\,\,\left( {-\infty ,\infty } \right)\)

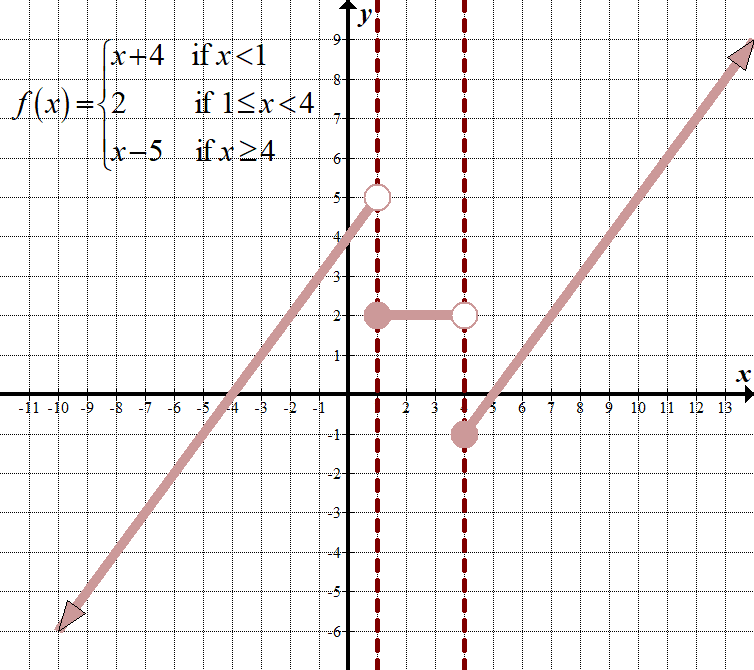We can actually put piecewise functions in the graphing calculator:

Piecewise Function Screens

Steps and Notes

Enter the piecewise function on three lines: Iată graficul:

pentru a pune funcția în bucăți \(\displaystyle F\stânga( x \dreapta)=\stânga\{ \începe{array}{L}x+4\,\,\,\,\,\,\,\,\,\text{if }x <1\\2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{dacă 1} \ le x < 4 \ \ -5 + x\,\,\,\,\,\text{dacă }x \ ge 4 \ end{matrice} \ dreapta.\ ) în calculator, puteți introduce funcția pe trei linii împărțind funcția în fiecare interval cu o „inegalitate de testare” a acelui interval (și urmăriți parantezele!). motivul pentru care împărțim la intervale sau inegalități este că calculatorul va returna un 1 dacă inegalitatea (cum ar fi \(X<1\)) este adevărată; de exemplu, \((x+4)\) va ajunge doar \((x+4)/(1)\) când \(x< 1\). Când \(x \ ge 1\), împărțim la 0, deci nimic nu va fi desenat. Iată ce putem pune în calculator: \(\displaystyle \begin{array}{l}{{Y}_{1}}=\stânga( {x+4} \dreapta)/\stânga( {x<1} \dreapta)\\{{y}_{2}}=\stânga( 2 \dreapta)/\stânga( {x\ge 1\text{ și }X<4} \right)\\{{y}_{3}}=\left( {-5+x} \right)/\left( {x\ge 4} \right)\end{array}\) (rețineți că puteți introduce și acest lucru pe o singură linie înmulțind condițiile în loc să împărțiți și folosind semne plus între fiecare dintre cele trei funcții/intervale: \(\displaystyle {{y}_{1}}=\stânga( {x+4} \dreapta)\stânga( {x<1} \dreapta)+\stânga( 2 \dreapta)\stânga( {x\ge 1\text{ și }x<4} \dreapta)+\stânga( {-5+x} \dreapta)\stânga( {x\ge 4} \dreapta)\).) Iată apăsările de taste pentru utilizarea a trei linii. Rețineți că utilizați 2nd MATH (TEST) pentru a ajunge la ecranul care are \(\le \), \(\ge \), și așa mai departe. De exemplu, 2nd MATH 6 devine \(\le \). Folosiți A 2-A matematică (TEST), dreptul la logică, apoi 1, pentru „și” în \({{y}_{2}}\).

cum să-i spuneți dacă funcția pe bucăți este continuă sau non-continuă

pentru a spune dacă un grafic pe bucăți este continuă sau non-continuă, trebuie poate să se uite la punctele de graniță și să vadă dacă punctul \(y\) este același la fiecare dintre ele. (Dacă \(y\) ‘ s au fost diferite, ar exista un „salt” în grafic!)

să încercăm acest lucru pentru funcțiile pe care le-am folosit mai sus:

Piecewise Function	Check Boundary Points
\(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}-2x+8\,\,\,\,\,\,\,\text{if }x\le 4\\\frac{1}{2}x-2\,\,\,\,\,\,\,\,\,\,\text{if }x>4\end{array} \right.\)	Let’s check \(x=4\) in both parts of the function, since 4 is the „boundary point”: \(\begin{array}{l}-2(4)+8=0\\\,\,\,\frac{1}{2}(4)-2=0\end{array}\) deoarece \(0=0\), această funcție în bucăți este continuă.
\ (\displaystyle F \ stânga (x \ dreapta)= \ stânga \ {\începe{array}{l}x+4\,\,\,\,\,\,\,\,\,\,\,\,\,\text{if }x <1\\2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{dacă 1} \ le x < 4 \ \ -5 + x\,\,\,\,\,\,\,\,\,\text{dacă }x \ ge 4 \ end{matrice} \ dreapta.\)	să verificăm primele două părți ale funcției. Notă în a doua parte, \(y\) este întotdeauna 2: \(\begin{array}{l}1+4=5\\\,\,\,\,\,\,\,\,\,2=2\end{array}\) deoarece \(5\ne 2\), ne putem opri aici, și rețineți că această funcție în bucăți este non-continuă. Dacă \(y\) – urile ar fi egale, ar trebui să mergem unul pentru a verifica următorul punct de graniță la \(x=4\).

obținerea ecuațiilor din graficele funcționale în bucăți

vi se poate cere să scrieți o funcție în bucăți, având în vedere un grafic. Acum, că știm despre ce sunt funcțiile în bucăți, nu este atât de rău!

pentru a examina modul de obținere a ecuațiilor din graficele liniare, consultați obținerea ecuațiilor unei linii și, din quadratică, vedeți găsirea unei ecuații pătratice din puncte sau un grafic.

aici sunt graficele, cu explicații cu privire la modul de a deriva ecuațiile lor în bucăți:

Piecewise Function Graph	Procedure to get Function
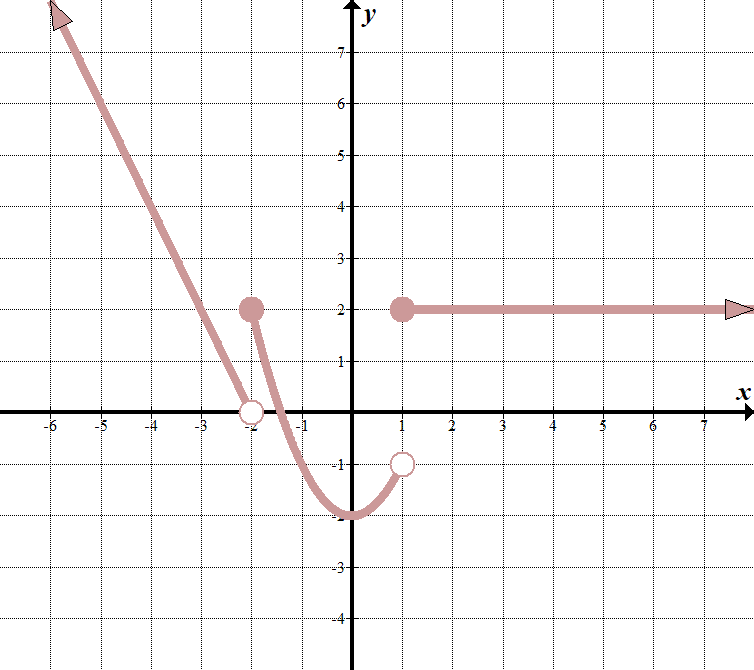	We see that our „boundary lines” are at \(x=-2\) and \(x=1\). We know that our function will look something like this (notice open and closed endpoints): \(\displaystyle F \ stânga (x \ dreapta)= \ stânga \ {\începe{array}{l} \ text{ }……\,\,\,\,\,\,\,\,\text{if }x <-2 \ \ \ text{ }……\,\,\,\,\,\,\,\,\text{if }-\text{2 }\le x<1 \ \ \ text{ }……\,\,\,\,\,\,\,\,\text{dacă }x \ ge 1 \ end{matrice} \ dreapta.\) putem alege două puncte \((-2,0)\) și \((-3,2)\) pe linia din stânga pentru a obține ecuația \(y=-2x-4\). funcția de mijloc este \(y = {{x}^{2}}-2\), și funcția din dreapta este doar linia orizontală \(y = 2\). astfel, funcția în bucăți este: \ (\displaystyle F \ stânga (x \ dreapta)= \ stânga \ {\începe{array}{l} – 2x-4\,\,\,\,\,\,\,\text{if }x <-2 \ \ \ text{ }{{x}^{2}}-2\,\,\,\,\,\,\,\,\,\,\text{if }-\text{2}\le x<1 \ \ \ text{ 2}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{dacă }x \ ge 1 \ end{matrice} \ dreapta.\)
	vedem că „linia noastră de graniță” este la \(x=5\). Deoarece liniile se întâlnesc la \((5,4)\), nu contează unde punem semnul \(\le \) sau \(\GE \) ; pur și simplu nu putem pune ambele locuri, sau nu ar fi o funcție. Avem până acum: \(\displaystyle F \ left (x \ right)= \ left \{\begin {array}{l} \ text{ }……\,\,\,\,\,\,\,\,\,\text{if }x <5 \ \ \ text{ }……\,\,\,\,\,\,\,\,\,\text{dacă }x \ ge 5 \ sfârșit{matrice} \ dreapta.\) Din nou, trebuie să ne uităm la fiecare linie separat pentru a determina ecuațiile lor. Putem lua fie 2 puncte de la fiecare linie pentru a obține aceste, sau derivă din pante și\(y\)–interceptează; funcția în bucăți este: \ (\displaystyle F \ stânga (x \ dreapta)= \ stânga \ {\începe{array}{l} \ frac{6}{5}x-2\,\,\,\,\,\,\,\text{dacă }x < 5 \ \ \ frac{2}{5}x+2\,\,\,\,\,\,\,\text{dacă }x \ ge 5 \ sfârșit{matrice} \ dreapta.\)

valoare absolută ca funcție în bucăți

putem scrie funcții de valoare absolută ca funcții în bucăți – este foarte cool! S-ar putea să doriți să revizuiți rezolvarea ecuațiilor de valoare absolută și a inegalităților înainte de a continua acest subiect.

Să presupunem că avem funcția \(f\stânga( x \dreapta)=\stânga|x \dreapta/\). Din ceea ce am învățat mai devreme, știm că atunci când \(x\) este pozitiv, deoarece luăm valoarea absolută, va fi în continuare doar \(x\). Dar când \(x\) este negativ, atunci când luăm valoarea absolută, trebuie să luăm opusul (să o negăm), deoarece valoarea absolută trebuie să fie pozitivă. Are sens? Deci, de exemplu, dacă am avea \(/5/\), luăm doar ceea ce este în interiorul semnului absolut, deoarece este pozitiv. Dar pentru \(/-5/\) , trebuie să luăm opusul (negativ) a ceea ce se află în interiorul valorii absolute pentru a-l face \(\displaystyle 5\,\,\,(-\,-5=5)\).

aceasta înseamnă că putem scrie această funcție de valoare absolută ca o funcție în bucăți. Observați că putem obține „punctul de cotitură” sau „punctul de graniță” setând orice se află în interiorul valorii absolute la 0. Apoi vom folosi funcția originală sau vom anula funcția, în funcție de semnul funcției (fără valoarea absolută) din acel interval.

de exemplu, putem scrie \(\displaystyle \ left / x \ right / \ text { } = \ left \{\begin{array}{l}x\,\,\,\,\,\,\,\,\,\text{dacă }x \ ge 0 \ \ – x\,\,\,\,\,\text{if }X <0\end{array} \dreapta.\). De asemenea, rețineți că, dacă funcția este continuă (nu există „salt”) la punctul de graniță, nu contează unde punem semnele „mai puțin sau egal cu” (sau „mai mare sau egal cu”), atâta timp cât nu le repetăm! Nu le putem repeta pentru că, teoretic, nu putem avea două valori ale lui \(y\) pentru același \(x\), altfel nu am avea o funcție.

Here are more examples, with explanations. (You might want to review Quadratic Inequalities for the second example below):

Absolute Value Function	Method to get Piecewise Function
\(g\left( x \right)=\left| {2x+3} \right|\)	Let’s first find the „boundary line”. Facem acest lucru setând ceea ce este în interiorul valorii absolute la 0 și apoi rezolvând pentru \(\boldsymbol{x}\). când \(2x+3\ge 0\), obținem \(\displaystyle x\ge -\frac{3}{2}\) (de fapt, putem păstra \(\ge \) când rezolvăm). Când \(2x + 3\) este pozitiv, îl luăm „așa cum este”, dar dacă este negativ, trebuie să negăm totul. prin urmare, funcția în bucăți este: \ (\displaystyle \ stânga / {2x + 3} \ dreapta / = \ stânga \ {\începe{array}{l}2x+3\,\,\,\,\,\,\,\,\,\text{dacă }x \ ge – \ frac{3}{2} \ text { } \ \ – 2x-3\,\,\,\,\,\text{if }X<-\frac{3}{2}\end{array} \dreapta.\) încercați – funcționează!
\(F\left( x \right)=\left| {{{x}^{2}}-4} \right|\)	să găsim mai întâi „linia de delimitare”; setăm ceea ce se află în valoarea absolută la 0. când \({{x}^{2}}-4 \ ge 0\), obținem \(x\le -2\) sau \(x\ge 2\) (încercați câteva numere!). Când \({{x} ^ {2}}-4\) este pozitiv, îl luăm „așa cum este”, dar dacă este negativ, trebuie să îl negăm. funcția pe bucăți este: \(\displaystyle \ left / {{{x} ^ {2}}-4} \ right / = \ left \ {\begin {array}{l}{{x}^{2}}-4\,\,\,\,\,\text{dacă }x \ le -2 \ \ 4 – {{x}^{2}}\,\,\,\,\,\text{if }-2<x< 2\\{{x}^{2}}-4\,\,\,\,\,\text{dacă }x \ ge 2 \ text { } \ sfârșit{matrice} \ dreapta.\ ) sau \(\displaystyle \ stânga / {{{x} ^ {2}}-4} \ dreapta / = \ stânga \ {\începe{array}{l}{{x}^{2}}-4\,\,\,\,\,\,\text{dacă }x \ le -2 \ text { }\,\, \text{or}\,\, \ text{ }x \ ge 2 \ \ 4 – {{x}^{2}}\,\,\,\,\,\,\,\text{if }-2<x<2\end{array} \dreapta.\) Din nou (deoarece funcția este continuă), chiar nu contează unde avem \(\le\) și \(\Ge\) (spre deosebire de \(<\) și \(>\)), atâta timp cât nu le repetăm.
\(F\stânga( x \dreapta)=2x+\stânga| {x+2} \dreapta|\)	acesta este un pic mai complicat, deoarece avem un \(x\) în interiorul și în afara valorii absolute. Pentru” linia de graniță”, folosim doar ceea ce se află în interiorul valorii absolute. când \(x + 2\ ge 0\), obținem\(x\ge -2\). Dar pentru funcția în bucăți, trebuie să folosim întreaga funcție, inclusiv partea care este în afara valorii absolute. Deci, funcția în bucăți este: \ (\displaystyle 2x + \ stânga / {x + 2} \ dreapta / = \ stânga\ {\începe{array}{l}2x + x+2\,\,\,\,\,\text{dacă }x \ ge -2 \ \ 2x-x-2\,\,\,\,\,\text{if }X <-2\end{array} \dreapta.\) să simplificăm: \(\displaystyle 2x + \ stânga / {x+2} \ dreapta / = \ stânga\ {\begin {array}{l}3x+2\,\,\,\,\,\,\,\text{dacă }x \ ge -2 \ \ x-2\,\,\,\,\,\,\,\,\,\,\text{if }X <-2\end{array} \dreapta.\ ) încercați unele valori mai puțin și mare atunci -2; acestea ar trebui să funcționeze!
\(g\left( x \right)=\left| {{{x}^{2}}-4x-5} \right|\)	acesta este cel mai bine rezolvat cu o diagramă de semne, deoarece avem un pătratic și trebuie să știm unde funcția este pozitivă și negativ. în primul rând, factorul pătratic din interiorul funcției de valoare absolută la \(\stânga( {x-5} \dreapta)\stânga( {x+1} \dreapta)\). Apoi folosiți o diagramă de semne pentru a vedea unde factorii sunt pozitivi și negativi și amintiți-vă că acolo unde factorii sunt pozitivi, folosim funcția „așa cum este”, iar unde factorii sunt negativi, negăm funcția: \(\displaystyle \stânga|{{{x}^{2}}-4x-5} \dreapta / =\stânga\{ \începe{array}{l}{{x}^{2}} – 4x-5\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{dacă }x\le -1\,\,\,\,\text{or}\,\,\,\, x \ ge 5\ \ – \ stânga ({{{x}^{2}}-4x-5} \ dreapta)\,\,\,\,\text{if }-1 <x<5\text{ }\end{array} \dreapta.\)
\(\displaystyle G\stânga( x \dreapta)=\frac{{\stânga| {x+2} \dreapta|}}{{x+2}}\)	aceasta este o funcție rațională, deoarece există o variabilă în numitor. când \(x + 2\ ge 0\), obținem \(\displaystyle x\ge -2\). Când \ (x + 2\) este pozitiv, îl luăm „așa cum este”, dar dacă este negativ, trebuie să negăm ceea ce este în valoarea absolută: \(\displaystyle \frac {{\left| {x+2} \ right/}} {{x+2}} = \ left \ {\begin {array}{l} \ frac{{x + 2}}{{x+2}}\,\,\,\,\,\,\,\,\,\text{dacă }x \ ge -2 \ \ \ frac {{- x-2}}{{x+2}}\,\,\,\,\,\,\text{if }X <-2\end{array} \dreapta.\). Dar trebuie să fim atenți, deoarece \(x \ ne 2\) (restricție de domeniu: numitorul ar fi 0). prin urmare, funcția în bucăți este: \(\displaystyle \ frac {{\stânga / {x + 2} \ dreapta/}} {{x + 2}}= \ stânga \ {\începe{array}{l}1\,\,\,\,\,\,\,\,\,\,\text{if }x >-2\\-1\,\,\,\,\,\,\text{if }X <-2\end{array} \dreapta.\).

De asemenea, vi se poate cere să luați un grafic de valoare absolută și să îl scrieți ca o funcție în bucăți:

Absolute Value Graph	Method to get Piecewise Function
	We see that our „boundary line” is at \(x=0\), so what’s inside the absolute value sign must be \(x\) or a factor of \(x\). (Acest lucru se datorează faptului că pentru a obține linia de graniță cu o funcție de valoare absolută, setăm ceea ce se află în interiorul valorii absolute la 0 și rezolvăm pentru \(x\)). când \(x>0\), putem vedea că ecuația liniei este \(y=2x-2\). Când \(x <0\), ecuația este \(y=2x-2\). Putem scrie acest lucru ca o funcție în bucăți: \(\displaystyle F\left( x \right)=\left\{ \begin{array}{l}2x-2\,\,\,\,\,\,\,\text{dacă }X>0\\-2x-2\,\,\,\text{dacă }x\le 0\end{matrice} \dreapta.\) de asemenea, putem scrie acest lucru ca o funcție de valoare absolută transformată: \(y=2\stânga|x \dreapta| -2\) sau \(y=\stânga|{2x} \dreapta| -2\) (deoarece 2 este pozitiv, poate fi în interiorul sau în afara \(\stânga|{ \ ,\,} \dreapta/\)). (Acest lucru are sens, deoarece atunci când ceea ce se află în interiorul \(\left| { \ ,\,} \right|\) este \(> 0\), folosim funcția regulată \(y=2x-2\) și când ceea ce se află în interiorul is \(< 0\), negăm partea de valoare absolută pentru a o face \(y=-\left( {2x} \dreapta)-2\)).
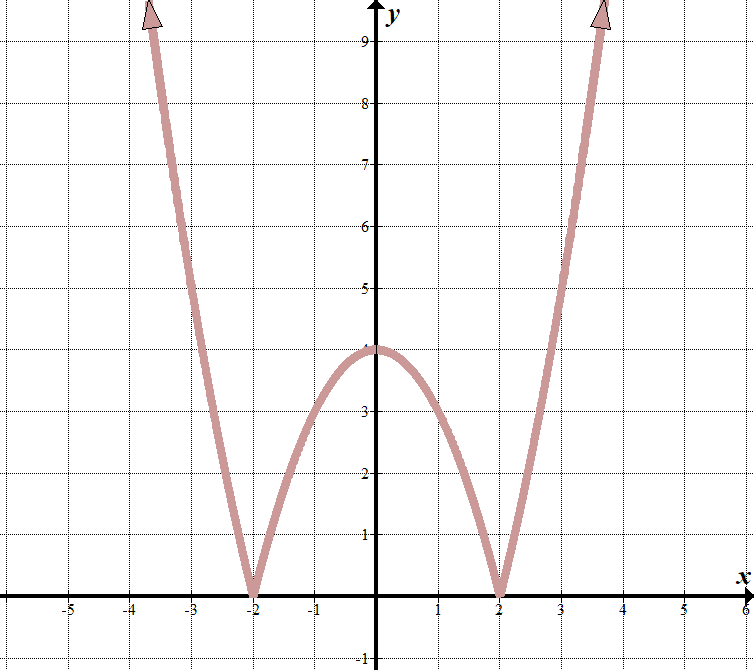	vedem că „liniile noastre limită” sunt la \(x=2\) și \(x=-2\), deci ceea ce se află în semnul valorii absolute trebuie să aibă factori de \(x-2\) și \(X+2\). când \ (x < -2\) sau \(X > 2\), putem vedea că graficul arată ca partea normală a graficului \(y = {{x}^{2}}-4\). (Mi-am dat seama de asta cunoscând factorii și luând o presupunere bună!) Când \(-2<x<2\), ecuația este oglindită sau negată (oglindită peste axa \(x\)). Putem scrie acest lucru ca o funcție în bucăți: \(\displaystyle F \ left (x \ right)= \ left \{\begin {array}{l}{{x}^{2}}-4\,\,\,\,\,\,\,\,\,\text{if }x <-2 \ text {or }x >2\\-{{x} ^ {2}} \ text{+ 4}\,\,\,\,\,\,\text{dacă }-2 \ le x \ le 2 \ end{matrice} \ dreapta.\) putem vedea că aceasta a început o funcție pătratică transformată \(y={{x}^{2}}-4\) cu o valoare absolută în jurul ei, deoarece toate valorile \(y\) sunt pozitive: \(y=\stânga|{{{x}^{2}}-4} \dreapta/\).
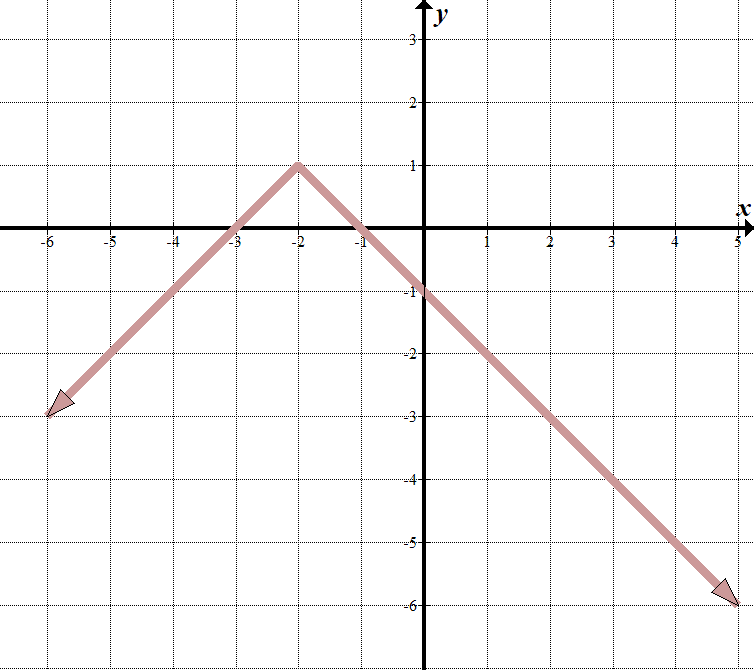	vedem că „linia noastră de graniță” este la \(x=-2\), deci ceea ce se află în semnul valorii absolute trebuie să fie \(x+2\). când \(x>-2\), putem vedea că ecuația liniei este \(y=-x-1\). Când \(x <-2\), linia este \(y=x+3\). Putem scrie acest lucru ca o funcție în bucăți: \(\displaystyle F\left( x \right)=\left\{ \begin{array}{l} – x-1\,\,\,\,\,\,\text{dacă }x > -2 \ \ x+3\,\,\,\,\,\,\,\,\,\,\text{dacă }x \ le -2 \ sfârșit{matrice} \ dreapta.\) este probabil mai ușor să scrieți acest lucru ca o funcție de valoare absolută transformată. Putem vedea că funcția de valoare absolută părinte este oglindită vertical, trece la stânga 2, și în sus 1. Ecuația noastră de valoare absolută este \(y= – \ stânga / {x + 2} \ dreapta|\,\,+\,\,1\). Aceasta este aceeași cu funcția în bucăți de mai sus. Încercați – funcționează!

transformări ale funcțiilor în bucăți

să facem o transformare a unei funcții în bucăți. Am aflat despre funcțiile părinte și transformările lor aici în secțiunea grafice și transformări părinte. Probabil că veți dori să citiți mai întâi această secțiune, înainte de a încerca o transformare în bucăți.

să transformăm următoarea funcție în bucăți rotită în jurul axei \(x\), întinsă vertical cu un factor de 2 unități, 1 unitate la dreapta și 3 unități în sus.

vom desena \(- 2F \ left (x-1 \right)+3\), unde:

\(\displaystyle F\left( x \right)=\left\{ \begin{align}x+4\,\,\,\,\,\,\,\,& \ text{ if }x <&\text{ dacă 1} \ le x< 4 \ \ x-5\,\,\,\,\,\,\,\,&\text{ if }x\ge 4\end{align} \dreapta.\ )

să ne asigurăm că folosim punctele „limită” atunci când completăm diagrama t pentru transformare. Amintiți-vă că transformările din paranteze se fac la \(x\) (făcând matematica opusă), iar în exterior se fac la \(y\). Pentru a veni cu o diagramă t, așa cum se arată în tabelul de mai jos, putem folosi puncte cheie, inclusiv două puncte pe fiecare dintre „liniile de graniță”.

rețineți că, deoarece această transformare este complicată, putem veni cu o nouă funcție în bucăți transformând cele 3 „bucăți” și transformând, de asemenea, „\(x\)”unde sunt punctele limită (adăugând 1 sau mergând la dreapta 1), deoarece facem matematica opusă pentru „\(x\)”. Pentru a obține noile funcții în fiecare interval, putem înlocui „\(x-1\)” Pentru „\(x\)” în ecuația inițială, înmulțiți cu -2, apoi adăugați 3. De exemplu, \(\displaystyle-2F\stânga( {x-1} \dreapta)+3=-2\stânga+3=-2\stânga( {x+3} \dreapta)+3=-2x-3\).

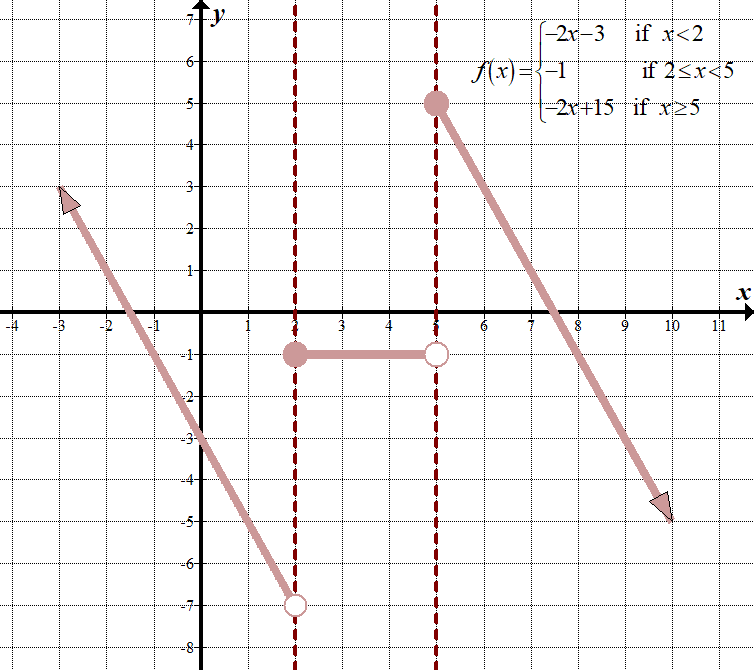
\ (\displaystyle-2F \ stânga ({x-1} \ dreapta)+3 = \ stânga \ {\începe {array}{l}-2 \ stânga ({\stânga ({x-1} \ dreapta) + 4} \ dreapta)+3 = – 2x-3,\,\,\,\,\text{ if }x-1<1\,\,\,\stânga( {x<2} \ dreapta) \ \ -2 \ stânga (2 \ dreapta)+3=-1,\,\,\,\,\text{ dacă }\, \ text{ 2} \ le x < 5 \ \ -2 \ stânga ({\stânga ({x-1} \ dreapta) -5} \dreapta)+3 = – 2x+15,\,\,\,\,\text{ dacă }x \ ge 5 \ sfârșit{matrice} \ dreapta.\)

aici sunt graficele „înainte” și „după”, inclusiv graficul t:

Piecewise Parent Function	T-chart	Transformation of Function
\(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}x+4\,\,\,\,\,\,\,\,\text{if }x<1\\2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{if 1 }\le x<4\\x-5\,\,\,\,\,\,\,\,\text{if }x\ge 4\end{array} \right.\)	x + 1 x y –2y+3 1 0 4 –5 2 1 5 –7 2 1 2 –1 5 4 2 –1 5 4 –1 5 8 7 2 –1	\(\displaystyle -2f\left( {x-1} \right)+3=\left\{ \begin{array}{l}-2x-3\,\,\,\,\,\,\,\,\,\text{if }x<2\\-1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{if 2}\le x<5\\-2x+15\,\,\,\,\,\,\text{if }x\ge 5\end{array} \right.\)

Piecewise Function Word Problems

Problem:

câinele tău preferat se încarcă în funcție de greutatea câinelui tău. Dacă câinele dvs. are 15 kilograme și mai puțin, groomerul percepe 35 USD. În cazul în care câinele este între 15 și 40 de lire sterline, ea percepe $40. Dacă câinele dvs. are peste 40 de lire sterline, ea percepe 40 de dolari, plus 2 dolari suplimentari pentru fiecare kilogram.

(a) scrieți o funcție în bucăți care descrie ceea ce încarcă îngrijitorul dvs. de câini.

(B) graficul funcției.

(c) CE ar taxa groomer dacă câinele dvs. drăguț cântărește 60 de kilograme?

soluție:

(a) vedem că „punctele limită” sunt 15 și 40, deoarece acestea sunt ponderile în care se schimbă prețurile. Din moment ce avem două puncte limită, vom avea trei ecuații în funcția noastră în bucăți. Trebuie să începem de la 0, deoarece câinii trebuie să cântărească peste 0 kilograme:

\ (\displaystyle F \ stânga (x \ dreapta)= \ stânga \ {\începe{array}{l} \ text{ }……\,\,\,\,\,\,\,\,\,\text{if }0 <x \ le 15 \ \ \ text{ }……\,\,\,\,\,\,\,\,\,\text{if }15 <x \ le 40 \ \ \ text{ }……\,\,\,\,\,\,\,\,\,\text{if }X >40\end{array} \dreapta.\)

căutăm „răspunsurile” (cât costă îngrijirea) la „întrebările” (cât cântărește câinele) pentru cele trei game de prețuri. Primele două sunt doar taxe fixe (35 USD, respectiv 40 USD). Ultima ecuație este puțin mai complicată; groomer percepe $ 40 plus $ 2 pentru fiecare lira peste 40. Să încercăm numere reale: în cazul în care câinele cântărește 60 de lire sterline, ea va percepe $40 plus $2 ori \(20(60-40)\). Vom transforma acest lucru într–o ecuație: \(40+2(x–40)\), care simplifică la \(2x-40\) (vezi cum 2 este panta?).

întreaga funcție în bucăți este:

\ (\displaystyle F \ stânga (x \ dreapta)= \ stânga \ {\începe{array}{l} \ text{ }35\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{if }0 <x \ le 15 \ \ \ text{ }40\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{if }15 <x \ le 40 \ \ \ text{ }40 + 2\stânga ({x-40} \ dreapta)\,\,\,\,\,\,\text{if }X >40\end{array} \dreapta.\ ) sau \ (\displaystyle F \ stânga (x \ dreapta)= \ stânga \ {\begin{array}{l} \ text{ }35\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{if }0 <x \ le 15 \ \ \ text{ }40\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{if }15 <x \ le 40 \ \ \ text{ }2x-40\,\,\,\,\,\,\,\text{if }X >40\end{array} \dreapta.\)

(b) să graficăm:rețineți că această ecuație în bucăți nu este continuă. De asemenea, rețineți că un domeniu rezonabil pentru această problemă ar putea fi \(\left( {0,200} \right]\) (având în vedere că câinii nu cântăresc peste 200 de kilograme!) și un interval rezonabil ar putea fi \(\left\cup \left\).

(c) dacă câinele dvs. cântărește 60 de kilograme, putem folosi fie graficul, fie funcția pentru a vedea că va trebui să plătiți 80 USD. Whoa! Asta costă mai mult decât o tunsoare umană (cel puțin tunsorile mele)!

problemă:

aveți de gând să vândă ea iubesc matematica tricouri ca o strangere de fonduri. Compania de tricouri cu ridicata vă percepe 10 USD pe cămașă pentru primele 75 de cămăși. După primele 75 de cămăși pe care le achiziționați până la 150 de cămăși, compania își va reduce prețul la 7,50 USD pe cămașă. După ce achiziționați 150 de cămăși, prețul va scădea la 5 USD pe cămașă. Scrieți o funcție care modelează această situație.

soluție:

vedem că „punctele de graniță” sunt 75 și 150, deoarece acestea sunt numărul de tricouri cumpărate unde se schimbă prețurile. Din moment ce avem două puncte limită, vom avea trei ecuații în funcția noastră în bucăți. Vom începe cu \(x \ ge 1\), deoarece, presupunem că cel puțin o cămașă este cumpărată. Notă în această problemă, Numărul de tricouri cumpărate (\(x\)) sau domeniul trebuie să fie un număr întreg, dar această restricție nu ar trebui să afecteze rezultatul problemei.

\(\displaystyle F\left( x \right)=\left\{ \begin{array}{l}\text{ }……\text{ if }1\le x\le 75\\text {}…..\text{ if }75<x\le 150\\\text {}……\text{ if }X>150\end{array}\dreapta.\)

căutăm „răspunsurile” (costul total al tricourilor) la „întrebările” (câte sunt cumpărate) pentru cele trei game de prețuri.

pentru până la 75 de cămăși inclusiv, prețul este de 10 USD, deci prețul total ar fi \(10x\). Pentru mai mult de 75 de cămăși, dar până la 100 de cămăși, costul este de 7,50 USD, dar primele 75 de tricouri vor costa în continuare 10 USD pe cămașă. A doua funcție include cei 750 de dolari cheltuiți pe primele 75 de cămăși (de 75 de ori 10 dolari) și include, de asemenea, de 7,50 de dolari numărul de cămăși peste 75, care ar fi \((x-75)\). De exemplu, dacă ați cumpărat 80 de cămăși, ar trebui să cheltuiți \(\$10 \ times 75= \ $ 750\), plus \(\$7.50\times 5\,\) (80 – 75) pentru cămășile de după cea de-a 75-a cămașă.

în mod similar, pentru peste 150 de cămăși, am plăti în continuare prețul de 10 USD prin 75 de cămăși, 7 dolari.50 preț pentru 76 până la 150 de cămăși (încă 75 de cămăși), apoi 5 USD pe cămașă pentru numărul de cămăși cumpărate peste 150. Vom plăti \(10(75)+7.50(75)+5(x-150)\) pentru \(X\) tricouri. Pune în numere și încercați să-l!

întreaga funcție în bucăți este:

\(\displaystyle F\left( x \right)=\left\{ \begin{array}{l}\text{ }10x\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{dacă }1 \ le x \ le 75 \ \ \ text{ }7,5 x \ text { } + \ text{ }187.5\,\,\,\,\,\text{Dacă 7}5 <x\le 150\\\text{ }5x+562.5\,\,\,\,\,\,\,\,\,\,\text{ if }X >150\end{array} \dreapta.\ ) sau \ (\displaystyle F \ stânga (x \ dreapta)= \ stânga \ {\începe{array}{l} \ text{ }10x\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{dacă }1 \ le x \ le 75 \ \ \ text{ }7,5 x \ text { } + \ text{ }187.5\,\,\,\,\,\text{Dacă 7}5 <x \ le 150 \ \ \ text{ }5x+562.5\,\,\,\,\,\,\,\,\,\,\,\text{if }X >150\end{array} \dreapta.\ )

problemă:

un serviciu de autobuz costă 50 USD pentru primele 400 de mile, iar fiecare 300 de mile suplimentare (sau o fracțiune din acestea) adaugă 10 USD la tarif.

utilizați o funcție în bucăți pentru a reprezenta tariful autobuzului în ceea ce privește distanța în mile.

soluție:

aceasta este de fapt o problemă dificilă, dar să ne gândim mai întâi mai întâi la „punctul de graniță”, care este 400. Este destul de simplu atunci când călătoria este mai mică de 400 de mile; costul este de 50 USD.

pentru mai mult de 400 de mile, trebuie să scădem primele 400 de mile (dar nu uitați să includeți primii 50 de dolari), Să împărțim numărul de mile rămase la 300 de mile (și să rotunjim, dacă există o sumă fracționată) și să înmulțim asta cu 10 dolari.

partea dificilă este atunci când ne „rotunjim” pentru o porțiune din următoarele 300 de mile. Putem folosi o funcție „plafon” (desemnată de \(\stânga\lceil {} \dreapta\rceil \)); această funcție oferă cel mai mic număr întreg care este mai mare sau egal cu intrarea sa; de exemplu, plafonul de 3,5 și 4 este 4.

astfel, aceasta este ceea ce avem:

\ (\displaystyle F \ stânga (x \ dreapta)= \ stânga \ {\începe{array}{l} \ text{ }50 \ text{ }\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{dacă }0 \ le x \ le 400 \ \ \ text{ }50 + 10 \ ori \ stânga \ iceil {\frac{{x-400}}{{300}}} \dreapta\rceil \ text{ }\,\,\,\,\,\,\text{ if }X >400\end{array} \dreapta.\)

să încercăm! Dacă avem o plimbare de 1500 de mile, costul ar fi \(\displaystyle 50 + 10 \ ori \ stânga \ iceil {\frac{{1500-400}}{{300}}} \dreapta\rceil \text { } = 50 + 10 \ ori 4 = \ $90\).

problema:

Ce valoare a \(\boldsymbol{a}\) ar face această funcție continuă?

\ (\displaystyle F \ stânga (x \ dreapta)= \ stânga \ {\începe{array}{l}3{{x}^{2}}+4\,\,\,\,\,\text{ if }x <-2 \ \ 5x + \ boldsymbol{a}\,\,\,\,\,\,\,\,\text{dacă }x \ ge -2 \ end{matrice} \ dreapta.\)

soluție:

pentru ca funcția în bucăți să fie continuă, la punctul limită (unde funcția se schimbă), cele două valori\ (y\) trebuie să fie aceleași. Putem conecta -2 pentru \(x\) în ambele funcții și asigurați-vă că \(y\)’s sunt aceleași

\(\begin {align}3{{x} ^ {2}} + 4 & = 5x + a \ \ 3 {{\stânga ({-2} \ dreapta)}^{2}}+4&=5\stânga( {-2} \dreapta)+a\\12+4&=-10+a\\a& = 26 \ end{align}\)

If \(a = 26\), funcția în bucăți este continuă!

învață aceste reguli și practică, practică, practică!

Mai multă practică: utilizați widgetul Mathway de mai jos pentru a încerca să scrieți o funcție în bucăți. Faceți clic pe Trimiteți (săgeata albastră din dreapta problemei) și faceți clic pe scrieți valoarea absolută în bucăți pentru a vedea răspunsul.

de asemenea, puteți introduce propria problemă sau faceți clic pe cele trei puncte din colțul din dreapta sus și faceți clic pe „exemple” pentru a detalia după subiect.

dacă faceți clic pe Atingeți pentru a vizualiza pașii sau faceți clic aici, vă puteți înregistra la Mathway pentru o încercare gratuită și apoi faceți upgrade la un abonament plătit în orice moment (pentru a rezolva orice tip de problemă de matematică!).

pe matrice și sisteme de rezolvare cu matrice – sunteți gata!