obiective de învățare

până la sfârșitul acestei secțiuni, veți putea:

• explica energia potențială gravitațională în termeni de muncă făcută împotriva gravitației.
• arată că energia potențială gravitațională a unui obiect de masă m la înălțimea h pe Pământ este dată de PEg = mgh.
• arată cum cunoașterea energiei potențiale în funcție de poziție poate fi utilizată pentru a simplifica calculele și a explica fenomenele fizice.

Figura 1. (a) munca depusă pentru ridicarea greutății este stocată în sistemul masă-pământ ca energie potențială gravitațională. (b) pe măsură ce greutatea se deplasează în jos, această energie potențială gravitațională este transferată la ceasul cu cuc.

Figura 2. Schimbarea energiei potențiale gravitaționale (Centipeg) între punctele A și B este independentă de traiectorie.

Exemplul 1. Forța de a opri care se încadrează

A 60.Persoana de 0 kg sare pe podea de la o înălțime de 3,00 m. dacă aterizează rigid (cu articulațiile genunchiului comprimându-se cu 0,500 cm), calculați forța asupra articulațiilor genunchiului.

strategie

energia acestei persoane este adusă la zero în această situație prin munca făcută pe el de podea în timp ce se oprește. Cuierul inițial este transformat în KE pe măsură ce cade. Munca făcută de podea reduce această energie cinetică la zero.

soluție

lucrarea efectuată asupra persoanei de la podea în timp ce se oprește este dată de W = FD cos (FD), cu semnul minus, deoarece deplasarea în timp ce se oprește și forța de la podea sunt în direcții opuse (cos (cos) = cos 180 (-1). Podeaua elimină energia din sistem, deci funcționează negativ.

energia cinetică pe care o persoană o are la atingerea podelei este cantitatea de energie potențială pierdută prin căderea prin înălțime h: KE = −Ecqupeg = −mgh.

distanța d pe care o îndoaie genunchii persoanei este mult mai mică decât înălțimea h a căderii, astfel încât schimbarea suplimentară a energiei potențiale gravitaționale în timpul îndoirii genunchiului este ignorată.

lucrarea w făcută de podea asupra persoanei oprește persoana și aduce energia cinetică a persoanei la zero: W = −KE = mgh.

combinând această ecuație cu expresia pentru W dă −Fd = mgh.

reamintind că h este negativ deoarece persoana a căzut, forța asupra articulațiilor genunchiului este dată de

\displaystyle{F}=-\frac{mgh}{d}=-\frac{\left(60.0\text{ kg}\dreapta)\stânga(9,80\text{ m/s}^2\dreapta)\stânga(-3,00\text{ m}\dreapta)}{5,00\times10^{-3}\text{ m}}=3,53\times10^5\text{ N}\\

discuție

o forță atât de mare (de 500 de ori mai mare decât greutatea persoanei) în timpul scurt de impact este suficientă pentru a rupe oasele. O modalitate mult mai bună de a amortiza șocul este îndoirea picioarelor sau rularea pe sol, mărind timpul în care acționează forța. O mișcare de îndoire de 0,5 m în acest fel produce o forță de 100 de ori mai mică decât în exemplu. Saltul unui cangur arată această metodă în acțiune. Cangurul este singurul animal mare care folosește saltul pentru locomoție, dar șocul în Salt este amortizat de îndoirea picioarelor posterioare la fiecare salt. (A Se Vedea Figura 3.)

Figura 3. Munca făcută de sol asupra cangurului reduce energia cinetică la zero pe măsură ce aterizează. Cu toate acestea, prin aplicarea forței solului pe picioarele posterioare pe o distanță mai mare, impactul asupra oaselor este redus. (credit: Chris Samuel, Flickr)

Exemplul 2. Găsirea vitezei unui roller Coaster de la înălțimea sa

1. care este viteza finală a roller coaster-ului prezentată în Figura 4 Dacă pornește de la odihnă în vârful dealului de 20,0 m și munca efectuată de forțele de frecare este neglijabilă?
2. care este viteza sa finală (presupunând din nou frecare neglijabilă) dacă viteza sa inițială este de 5,00 m/s?

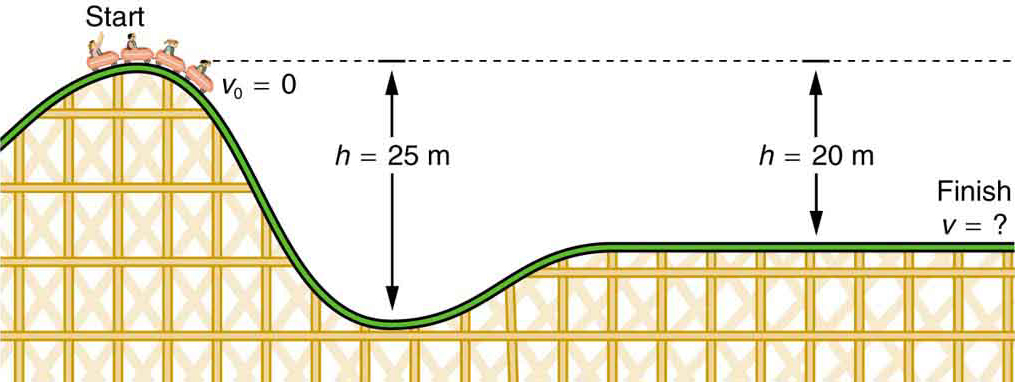
Figura 4. Viteza unui roller coaster crește pe măsură ce gravitația o trage în jos și este cea mai mare în punctul său cel mai de jos. Privit din punct de vedere energetic, energia potențială gravitațională a sistemului roller-coaster-Pământ este transformată în energie cinetică. Dacă munca efectuată prin frecare este neglijabilă, toate Centipeg sunt convertite în ke.

strategie

roller coaster pierde energie potențială pe măsură ce coboară. Neglijăm frecarea, astfel încât forța rămasă exercitată de pistă este forța normală, care este perpendiculară pe direcția de mișcare și nu funcționează. Lucrarea netă pe roller coaster se face apoi numai prin gravitație. Pierderea energiei potențiale gravitaționale din deplasarea în jos printr-o distanță h este egală cu câștigul de energie cinetică. Acest lucru poate fi scris în formă de ecuație ca −Zifktpeg = ZIFKTKE. Folosind ecuațiile pentru PEg și KE, putem rezolva pentru viteza finală v, care este cantitatea dorită.

soluție pentru partea 1

aici energia cinetică inițială este zero, astfel încât \Delta\text{KE}=\frac{1}{2}mV^2\\. Ecuația pentru schimbarea energiei potențiale afirmă că Ecqupeg = mgh. Deoarece h este negativ în acest caz, vom rescrie acest lucru ca Unqqupeg = −mg|h| pentru a arăta clar semnul minus. Astfel, – Unktifpeg = UNKTIFKE devine mg / h/= \ frac{1}{2}{mv}^2\\.

rezolvând pentru v, descoperim că masa se anulează și că v=\sqrt{2G|h/}\\.

înlocuind valorile cunoscute,

\begin{array}{lll}v&&\sqrt{2\stânga(9.80\text{ m/s}^2\dreapta)\stânga(20.0\text{ m}\right)}\\\text{ }&&19.8\text{ m/s}\End{array}\\

soluție pentru partea 2

din nou −inktiptpeg = inktke. În acest caz există energie cinetică inițială, deci

\Delta\text{KE}=\frac{1}{2}mV^2-\frac{1}{2}mv_0^2\\.

astfel, mg|h / =\frac{1}{2}mV^2-\frac{1}{2}mv_0^2\\.

rearanjarea dă \frac{1}{2}mV^2=mg|h / +\frac{1}{2}mv+0^2\\.

aceasta înseamnă că energia cinetică finală este suma energiei cinetice inițiale și a energiei potențiale gravitaționale. Masa anulează din nou, și v=\sqrt{2G|h|+v_0^2}\\.

această ecuație este foarte asemănătoare cu ecuația cinematică v=\sqrt{v_0^2+2AD}\\, dar este mai generală—ecuația cinematică este valabilă numai pentru accelerația constantă, în timp ce ecuația noastră de mai sus este valabilă pentru orice cale, indiferent dacă obiectul se mișcă cu o accelerație constantă. Acum, înlocuind valorile cunoscute dă

\begin{array}{lll}v&&\sqrt{2\stânga(9.80\text{ m/s}^2\dreapta)\stânga(20.0\text{ m}\dreapta)+\stânga(5.00\text{ m/s}\dreapta)^2}\\\text{ }&&20.4\text{ m/s}\end{array}\ \

discuție și implicații

Mai întâi, rețineți că masa se anulează. Acest lucru este în concordanță cu observațiile făcute în obiecte care se încadrează că toate obiectele cad în același ritm dacă fricțiunea este neglijabilă. În al doilea rând, este luată în considerare doar viteza roller coaster-ului, nu există informații despre direcția sa în niciun moment. Acest lucru dezvăluie un alt adevăr general. Când fricțiunea este neglijabilă, viteza unui corp care cade depinde doar de viteza și înălțimea sa inițială, și nu de masa sau de calea parcursă. De exemplu, roller coaster-ul va avea aceeași viteză finală, indiferent dacă cade 20,0 m drept în jos sau ia o cale mai complicată ca cea din figură. În al treilea rând, și poate în mod neașteptat, viteza finală din partea 2 este mai mare decât în partea 1, dar cu mult mai mică de 5,00 m/s. în cele din urmă, rețineți că viteza poate fi găsită la orice înălțime de-a lungul drumului prin simpla utilizare a valorii corespunzătoare a lui h în punctul de interes.

realizarea conexiunilor: investigație la domiciliu-conversia potențialului în energie cinetică

se poate studia conversia energiei potențiale gravitaționale în energie cinetică în acest experiment. Pe o suprafață netedă, plană, utilizați o riglă de tipul care are o canelură care rulează de-a lungul lungimii sale și o carte pentru a face o înclinație (vezi Figura 5). Așezați o marmură în poziția de 10 cm pe riglă și lăsați-o să se rostogolească pe riglă. Când atinge suprafața plană, măsurați timpul necesar pentru a rula un metru. Acum așezați marmura în pozițiile de 20 cm și 30 cm și măsurați din nou timpii necesari pentru a rula 1 m pe suprafața plană. Găsiți viteza marmurei pe suprafața plană pentru toate cele trei poziții. Viteza parcelei pătrat față de distanța parcursă de marmură. Care este forma fiecărui complot? Dacă forma este o linie dreaptă, graficul arată că energia cinetică a marmurei în partea de jos este proporțională cu energia sa potențială la punctul de eliberare.

Figura 5. O marmură se rostogolește pe o riglă, iar viteza sa pe suprafața plană este măsurată.

1. În exemplul 2, am calculat viteza finală a unui roller coaster care a coborât 20 m înălțime și a avut o viteză inițială de 5 m/s în jos. Să presupunem că roller coaster-ul a avut o viteză inițială de 5 m/s în sus și a coborât în sus, s-a oprit și apoi s-a rostogolit înapoi până la un punct final la 20 m sub start. Ne-ar găsi în acest caz, că a avut aceeași viteză finală. Explicați în termeni de conservare a energiei.
2. munca pe care o faci pe o carte atunci când o ridici pe un raft depinde de calea luată? La timpul necesar? Pe înălțimea raftului? Pe masa cărții?

probleme& exerciții

1. o instalație hidroelectrică (vezi Figura 6) transformă energia potențială gravitațională a apei din spatele unui baraj în energie electrică. (a) care este energia potențială gravitațională în raport cu generatoarele unui lac cu volumul 50.0 km3 (masa = 5.00 1013 kg), in conditiile in care lacul are o inaltime medie de 40.0 m deasupra generatoarelor? (B) comparați acest lucru cu energia stocată într-o bombă de fuziune de 9 megatone.
   

   Figura 6. Facilitatea hidroelectrică (credit: Denis Belevich, Wikimedia Commons)

2. (a) câtă energie potențială gravitațională (în raport cu solul pe care este construită) este stocată în Marea Piramidă a lui Cheops, având în vedere că masa sa este de aproximativ 7 109 kg și centrul său de masă este de 36.5 m deasupra solului înconjurător? b) cum se compară această energie cu consumul zilnic de alimente al unei persoane?
3. Să presupunem că un kookaburra de 350 g (o pasăre mare de pescăruș) ridică un șarpe de 75 g și îl ridică la 2,5 m de la sol la o ramură. a) câtă muncă a făcut pasărea asupra șarpelui? b) câtă muncă a depus pentru a-și ridica propriul centru de masă la ramură?
4. în exemplul 2, am constatat că viteza unui roller coaster care a coborât cu 20,0 m a fost doar puțin mai mare atunci când a avut o viteză inițială de 5,00 m/s decât atunci când a pornit de la odihnă. Acest lucru implică faptul că >> KEi. Confirmați această afirmație luând raportul dintre XIXTPE și KEi. (Rețineți că masa anulează.)
5. o mașină de jucărie de 100 g este propulsată de un arc comprimat care o pornește în mișcare. Mașina urmează pista curbată din Figura 7. Arătați că viteza finală a mașinii de jucărie este de 0,687 m/s dacă viteza inițială este de 2,00 m/s și se deplasează pe panta fără frecare, câștigând 0,180 m altitudine.
   

   Figura 7. O mașină de jucărie se deplasează pe o pistă înclinată. (credit: Leszek Leszczynski, Flickr)

6. într-o cursă de schi alpin, în mod surprinzător, se obține un mic avantaj prin obținerea unui start de alergare. (Acest lucru se datorează faptului că energia cinetică inițială este mică în comparație cu câștigul de energie potențială gravitațională chiar și pe dealuri mici.) Pentru a demonstra acest lucru, găsiți viteza finală și timpul necesar pentru un schior care schiază 70,0 m de-a lungul unei pârtii de 30 de centimi neglijând frecarea: (a) pornind de la odihnă. (b) începând cu o viteză inițială de 2,50 m/s. (c) vă surprinde răspunsul? Discutați de ce este încă avantajos să începeți să alergați în evenimente foarte competitive.

soluții selectate la probleme& exerciții

1. (a) 1,96 int 1016 J; (B) raportul dintre energia potențială gravitațională din lac și energia stocată în bombă este de 0,52. Adică, energia stocată în lac este de aproximativ jumătate din cea a unei bombe de fuziune de 9 megatone.

3. (a) 1,8 J; (b) 8,6 J

5. {v} _ {f}= \ sqrt{2GH + {v_0}^2} = \sqrt{2 \ stânga (9.80 \ text{ m / s}^2 \ dreapta) \ stânga (-0.180 \ text{ m}\dreapta)+\stânga(2.00\text{ m/s}\dreapta)^2}=0.687\text{ m/s}\ \