după înțelegerea funcției exponențiale, următoarea noastră țintă este logaritmul natural.

având în vedere modul în care jurnalul natural este descris în cărțile de matematică, există puține „naturale” despre el: este definit ca inversul lui $e^x$, un exponent destul de ciudat deja.

dar există o explicație nouă, intuitivă: jurnalul natural vă oferă timpul necesar pentru a atinge un anumit nivel de creștere.

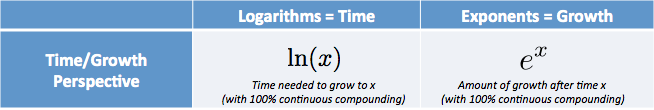
Să presupunem că aveți o investiție în urși gumosi (cine nu?) cu o rată a dobânzii de 100% pe an, în creștere continuă. Dacă doriți o creștere de 10x, presupunând o compunere continuă, ați aștepta doar $\ln(10)$ sau 2.302 ani. Nu vedeți de ce durează doar câțiva ani pentru a obține o creștere de 10 ori? Nu vedeți de ce modelul nu este 1, 2, 4, 8? Citiți mai multe despre e.

e și jurnalul Natural sunt gemeni:

• $e^X$ este suma pe care o avem după ce începem de la 1.0 și în creștere continuă pentru $X $ unități de timp
• $\ln (x)$ (logaritm Natural) este timpul pentru a ajunge la suma $x$, presupunând că am crescut continuu de la 1.0

nu prea rău, nu? În timp ce matematicienii se luptă pentru a vă oferi explicația tehnică lungă, să ne scufundăm în cea intuitivă.

E este despre creștere

numărul e este despre creștere continuă. După cum am văzut ultima dată, $e^x$ ne permite să fuzionăm rata și timpul: 3 ani la o creștere de 100% este aceeași cu 1 an la o creștere de 300%, când este agravată continuu.

putem lua orice combinație de rată și timp (50% timp de 4 ani) și să convertim rata la 100% pentru comoditate (oferindu-ne 100% timp de 2 ani). Prin conversia la o rată de 100%, trebuie doar să ne gândim la componenta de timp:

intuitiv, $e^x$ înseamnă:

• câtă creștere primesc după X unități de timp (și 100% creștere continuă)
• de exemplu: după 3 perioade de timp am $e^3$ = 20,08 ori cantitatea de „chestii”.

$e^X$ este un factor de scalare, care ne arată cât de multă creștere am obține după unitățile de timp $x$.

jurnalul Natural este despre timp

jurnalul natural este inversul lui $e^x$, un termen fantezist pentru opus. Vorbind de fantezie, numele Latin este logarithmus naturali, dând abrevierea ln.

ce înseamnă aceste lucruri inverse sau opuse?

• $e^x$ ne permite să conectăm timpul și să obținem o creștere.
• $ \ ln( x) $ ne permite să conectăm creșterea și să obținem timpul necesar.

de exemplu:

• $e^3$ este 20,08. După 3 unități de timp, ajungem la 20.08 ori ceea ce am început cu.
• $\ln (20.08)$ este de aproximativ 3. Dacă dorim o creștere de 20.08, am aștepta 3 unități de timp (din nou, presupunând o rată de creștere continuă de 100%).

cu mine? Jurnalul natural ne oferă timpul necesar pentru a atinge creșterea dorită.

aritmetica logaritmică nu este normală

ați studiat jurnalele înainte și erau fiare ciudate. Cum au transformat înmulțirea în adunare? Împărțirea în scădere? Să vedem.

ce este $\ln (1)$? Intuitiv, întrebarea este: cât timp aștept pentru a obține 1x suma mea curentă?

Zero. Zip. Nimic. Sunteți deja la 1x suma curentă! Nu este nevoie de timp pentru a crește de la 1 la 1.

• $\ln(1) = 0$

OK, ce zici de o valoare fracționată? Cât timp pentru a obține 1/2 suma mea curentă? Presupunând că creșteți continuu la 100%, știm că $\ln(2)$ este timpul de dublare. Dacă o inversăm (adică luăm timpul negativ), am avea jumătate din valoarea noastră actuală.

• $\ln(.5) = – \ln(2)= -.693$

are sens, nu? Dacă mergem înapoi .693 de unități (secunde negative, să zicem) am avea jumătate din suma noastră actuală. În general, puteți răsturna fracția și puteți lua negativul: $\ln(1/3) = – \ln(3) = -1,09$. Aceasta înseamnă că dacă ne întoarcem cu 1,09 unități de timp, am avea o treime din ceea ce avem acum.

OK, ce zici de jurnalul natural al unui număr negativ? Cât timp este nevoie pentru a „crește” colonia de bacterii de la 1 la -3?

este imposibil! Nu poți avea o cantitate” negativă ” de bacterii, nu-i așa? Cel mult (er… cel puțin) puteți avea zero, dar nu există nicio modalitate de a avea o cantitate negativă de creaturi mici. Bacteriile Negative nu au sens.

• $\ln(\text{număr negativ}) = \text{undefined}$

Undefined înseamnă doar „nu există nici o cantitate de timp puteți aștepta” pentru a obține o sumă negativă. (Ei bine, dacă folosim exponențiale imaginare, există o soluție. Dar astăzi să o păstrăm reală.)

înmulțirea logaritmică este foarte distractivă

cât durează să crești de 9 ori suma curentă? Sigur, am putea folosi doar ln (9). Dar asta e prea ușor, să fim diferiți.

putem considera creșterea de 9x ca triplare (luând $\ln (3) $ unități de timp) și apoi triplare din nou (luând încă $\ln (3)$ unități de timp):

• timp pentru a crește 9x = $\ln(9)$ = timp pentru a tripla și Tripla din nou = $\ln(3) + \ln(3)$

interesant. Orice număr de creștere, cum ar fi 20, poate fi considerat 2x creștere urmată de 10x creștere. Sau 4x creștere urmată de 5x creștere. Sau 3x creștere urmată de 6.666 x creștere. Vezi modelul?

• $\ln(a*b) = \ln(a) + \ln(b)$

Jurnalul de a ori b = log(a) + log(b). Această relație are sens atunci când te gândești în termeni de timp pentru a crește.

dacă vrem să creștem 30x, putem aștepta $\ln(30)$ dintr-o dată, sau pur și simplu așteptăm $\ln(3)$, pentru a tripla, apoi așteptați $\ln(10)$, pentru a crește din nou 10x. Efectul net este același, deci timpul net ar trebui să fie același (și este).

Ce zici de diviziune? $\ln (5/3)$ înseamnă: cât timp durează să crească de 5 ori și apoi să ia 1/3 din asta?

Ei bine, creșterea de 5 ori este $\ln(5)$. Creșterea 1/3 este $ – \ln (3) $ unități de timp. Deci

• $\ln(5/3) = \ln(5) – \ln(3)$

care spune: creșteți de 5 ori și „întoarceți-vă în timp” până când aveți o treime din această sumă, deci rămâneți cu o creștere de 5/3. În general avem

• $\ln(a/b) = \ln(a) – \ln(b)$

sper că matematica ciudată a logaritmilor începe să aibă sens: înmulțirea creșterii devine adăugarea timpului, împărțirea creșterii devine scăderea timpului. Nu memorați regulile, înțelegeți-le.

folosind jurnalele naturale cu orice rată

„sigur”, spui tu, „chestia asta cu jurnalele funcționează pentru o creștere de 100%, dar ce zici de cei 5% pe care îi obțin în mod normal?”

nu este nicio problemă. „Timpul „pe care îl primim înapoi de la $\ln()$ este de fapt o combinație de rată și timp,” x ” din ecuația noastră $e^x$. Presupunem doar 100% pentru a face simplu, dar putem folosi alte numere.

Să presupunem că vrem o creștere de 30x: conectați $\ln (30)$ și obțineți 3,4. Aceasta înseamnă:

• $e^x = \text{growth}$
• $e^{3.4} = 30$

și intuitiv această ecuație înseamnă „randamentul 100% pentru 3,4 ani este o creștere de 30x”. Putem considera ecuația ca fiind:

putem modifica „rata” și „timpul”, atâta timp cât rata * timpul = 3.4. De exemplu, să presupunem că dorim o creștere de 30 de ori-cât timp așteptăm presupunând o rentabilitate de 5%?

• $\ln (30) = 3.4$
• $\text{rata} * \text{Timp} = 3.4$
• $.05 * \ text{timp} = 3.4$
• $ \ text{timp} = 3.4/.05 = 68\text{years}$

intuitiv, cred că „$ \ ln(30) = 3,4$, deci la o creștere de 100% va dura 3,4 ani. Dacă dublez rata de creștere, reduc la jumătate timpul necesar.”

• 100% pentru 3,4 ani = 1,0 * 3,4 = 3,4
• 200% pentru 1,7 ani = 2,0 * 1,7 = 3,4
• 50% pentru 6,8 ani = 0,5 * 6,8 = 3,4
• 5% pentru 68 ani = .05 * 68 = 3.4

Cool, nu? Jurnalul natural poate fi utilizat cu orice rată a dobânzii sau timp, atâta timp cât produsul lor este același. Puteți wiggle variabilele tot ce vrei.

exemplu minunat: regula de 72

regula de 72 este o scurtătură matematică mentală pentru a estima timpul necesar pentru a vă dubla banii. O să-l derivăm (yay!) și chiar mai bine, o vom înțelege intuitiv.

cât timp este nevoie pentru a dubla banii la 100% interes, agravată în fiecare an?

Uh oh. Am folosit jurnalul natural pentru rate continue, dar acum ceri dobândă anuală? Asta nu ne va strica formula? Da, va fi, dar la rate ale dobânzii rezonabile, cum ar fi 5%, 6% sau chiar 15%, nu există prea multe diferențe între dobânda anuală compusă și cea continuă. Deci formula dur funcționează, uh, aproximativ și ne vom preface că suntem obtinerea interes pe deplin continuă.

acum întrebarea este ușor: cât timp să se dubleze la 100% interes? ln(2) = .693. Este nevoie .693 de unități de timp (Ani, în acest caz) pentru a vă dubla banii cu o compunere continuă cu o rată de 100%.

Ok, ce se întâmplă dacă interesul nostru nu este de 100% ce se întâmplă dacă este de 5% sau 10%?

simplu. Atâta timp cât rata * timp = .693, ne vom dubla banii:

• rata * timp = .693
• timp = .693 / rata

deci, dacă am avea doar o creștere de 10%, ar fi nevoie .693 / .10 sau 6,93 ani să se dubleze.

pentru a simplifica lucrurile, să înmulțim cu 100 astfel încât să putem vorbi despre 10, mai degrabă decât .10:

• timpul de dublare = 69,3 / rată, unde se presupune că rata este în procente.

acum, momentul dublării la o creștere de 5% este de 69,3 / 5 sau 13,86 ani. Cu toate acestea, 69.3 nu este numărul cel mai divizibil. Să alegem un vecin apropiat, 72, care poate fi împărțit la 2, 3, 4, 6, 8 și multe alte numere.

• timp pentru a dubla = 72 / rata

care este regula de 72! Ușor breezy.

Dacă doriți să găsiți timp pentru a tripla, veți folosi ln(3) ~ 109.8 și veți obține

• timp pentru a tripla = 110/rata

care este o altă regulă utilă. Regula de 72 este utilă pentru ratele dobânzilor, creșterea populației, culturile de bacterii și orice crește exponențial.

unde de aici?

sper că jurnalul natural are mai mult sens — vă spune timpul necesar pentru orice cantitate de creștere exponențială. Consider că este ” natural „pentru că e este rata universală de creștere, așa că ln ar putea fi considerat modul” universal ” de a afla cât durează lucrurile să crească.

când vedeți $\ln(x)$, gândiți-vă doar la „cantitatea de timp pentru a crește la x”. În articolul următor vom aduce e și ln împreună, iar aroma dulce a matematicii va umple aerul.

apendice: jurnalul Natural al E

quiz rapid: ce este $\ln (e)$?

• robotul matematica spune: deoarece acestea sunt definite a fi funcții inverse, în mod clar $\ln (e) = 1$
• uman intuitiv: ln (e) este cantitatea de timp necesară pentru a obține unități de creștere „e” (aproximativ 2.718). Dar e este cantitatea de creștere după 1 unitate de timp, deci $\ln(e) = 1$.

gândiți intuitiv.

alte posturi din această serie

1. Un ghid intuitiv pentru funcțiile exponențiale& e
2. demistificarea logaritmului Natural (ln)
3. Un ghid vizual pentru ratele dobânzilor simple, compuse și continue
4. definiții comune ale e (Colorizat)
5. înțelegerea exponenților (de ce 0^0 = 1?)
6. folosind logaritmi în lumea reală
7. cum să gândești cu exponenți și logaritmi
8. înțelegerea creșterii Discrete vs. continue
9. ce înseamnă cu adevărat un exponent?
10. Î: De ce este e special? (2.718…, nu 2, 3,7 sau alt număr?)