în alte secțiuni s-a menționat că multe dintre proprietățile solidelor, lichidelor și gazelor ar putea fi contabilizate dacă am presupune că substanțele sunt formate din atomi sau molecule care sunt în continuă mișcare. Legea lui Boyle și celelalte legi ale gazelor ne-au oferit acum mult mai multe informații cantitative despre gaze și merită să ne întrebăm dacă cu modelul anterior putem face predicții cantitative în acord cu aceste legi. Răspunzând la această întrebare, vom obține, de asemenea, informații importante despre natura temperaturii și a energiei termice.teoria microscopică a comportamentului gazelor bazată pe mișcarea moleculară se numește teoria cinetică a gazelor. Postulatele sale de bază sunt enumerate în tabelul 1:

tabelul \(\PageIndex{1}\) postulatele teoriei cinetice a gazelor.

1 moleculele dintr-un gaz sunt mici și foarte îndepărtate. Cea mai mare parte a volumului pe care îl ocupă un gaz este spațiu gol.

2 molecule de gaz sunt în mișcare aleatorie constantă. La fel cum multe molecule se mișcă într-o direcție ca în oricare alta.

3 molecule se pot ciocni între ele și cu pereții recipientului. Coliziunile cu pereții reprezintă presiunea gazului.

4 Când apar coliziuni, moleculele nu pierd energie cinetică; adică se spune că coliziunile sunt perfect elastice. Energia cinetică totală a tuturor moleculelor rămâne constantă, cu excepția cazului în care există o interferență exterioară cu

5 moleculele nu exercită forțe atractive sau respingătoare una asupra celeilalte, cu excepția procesului de coliziune. Între coliziuni, se mișcă în linii drepte.

din ele este posibil să se deducă următoarea expresie pentru presiunea unui gaz în ceea ce privește proprietățile moleculelor sale:

\ unde P, V = presiunea și volumul gazului

N = numărul de molecule

m = masa fiecărei molecule

(u2)ave = media (sau media) pătratelor tuturor vitezelor moleculare individuale. Această viteză medie pătrată trebuie utilizată deoarece presiunea este proporțională cu pătratul vitezei moleculare, iar coliziunile moleculare determină diferite molecule să aibă viteze destul de diferite.

mai degrabă decât să ne preocupe de procedura de derivare a Eq. \(\ref{1}\), să inspectăm ecuația și să vedem că trăsăturile sale generale sunt așa cum ne-am aștepta. În unele moduri, capacitatea de a face acest lucru cu o formulă este mai utilă decât capacitatea de a o obține. Figura \(\PageIndex{1}\)

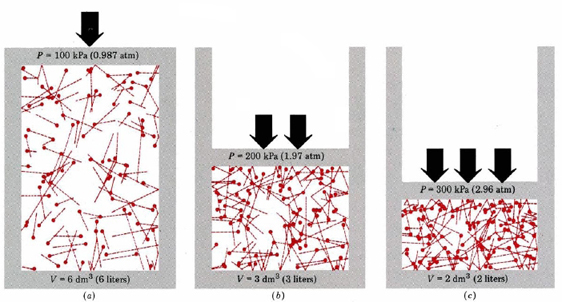în primul rând, ecuația ne spune că presiunea unui gaz este proporțională cu numărul de molecule împărțit la volum. Acest lucru este prezentat grafic în figura \(\PageIndex{1}\), unde un computer a atras același număr de molecule de gaz care ocupă fiecare din cele trei volume diferite. „Coada” de pe fiecare moleculă arată calea exactă urmată de acea moleculă în microsecunda anterioară—cu cât coada este mai lungă, cu atât molecula mergea mai repede. Media pătratelor lungimilor cozii este proporțională cu (u2)ave și este aceeași în toate cele trei diagrame. De asemenea, se presupune că toate moleculele au mase egale.

după cum puteți vedea, reducerea volumului de gaz crește numărul de coliziuni pe unitatea de suprafață pe pereții containerului. Fiecare coliziune exercită forță pe perete; forța pe unitate de suprafață este presiune, astfel încât numărul de coliziuni pe unitate de suprafață este proporțional cu presiunea. Reducerea la jumătate a volumului dublează presiunea, o predicție care este de acord cu faptele experimentale rezumate în Legea lui Boyle. Ecuația \(\ref{1}\) spune, de asemenea, că presiunea este proporțională cu masa fiecărei molecule de gaz. Din nou, aceasta este ceea ce ne-am aștepta. Moleculele grele dau o „împingere”mai mare(termenul tehnic pentru aceasta este impuls) împotriva peretelui decât cele ușoare cu aceeași viteză. în cele din urmă, ecuația ne spune că presiunea este proporțională cu media pătratelor vitezelor moleculare. Această dependență de pătratul vitezei este rezonabilă dacă ne dăm seama că dublarea vitezei unei molecule are două efecte.în primul rând, molecula se poate deplasa mai departe într-o anumită perioadă de timp, dublând numărul de coliziuni cu pereții. Acest lucru ar dubla presiunea. În al doilea rând, dublarea vitezei unei molecule dublează împingerea sau impulsul fiecărei coliziuni. Acest lucru dublează din nou presiunea. Prin urmare, dublarea vitezei unei molecule cvadruplează presiunea, iar pentru un număr mare de molecule, P este proporțional cu viteza medie pătrată.