orbitali atomici
un orbital este rafinamentul mecanic cuantic al orbitei lui Bohr. Spre deosebire de conceptul său de orbită circulară simplă cu o rază fixă, orbitalii sunt regiuni ale spațiului derivate matematic cu probabilități diferite de a avea un electron.
o modalitate de reprezentare a distribuțiilor de probabilitate a electronilor a fost ilustrată în figura 6.5.2 pentru orbitalul 1s al hidrogenului. Deoarece xc2 dă probabilitatea de a găsi un electron într-un anumit volum de spațiu (cum ar fi un picometru cubic), un complot de xc2 față de Distanța de la nucleu (r) este un complot al densității probabilității. Orbitalul 1s este simetric sferic, astfel încât probabilitatea de a găsi un electron 1S în orice punct dat depinde doar de Distanța sa de nucleu. Densitatea probabilității este cea mai mare la r = 0 (la nucleu) și scade constant odată cu creșterea distanței. La valori foarte mari ale lui r, densitatea probabilității electronilor este foarte mică, dar nu zero.
în contrast, putem calcula probabilitatea radială (probabilitatea de a găsi un electron 1s la o distanță r de nucleu) prin adăugarea împreună a probabilităților unui electron care se află în toate punctele pe o serie de cochilii sferice X de rază r1, r2, r3,…, rx − 1, rx. De fapt, împărțim atomul în cochilii concentrice foarte subțiri, la fel ca straturile unei cepe (partea (a) din Figura \(\PageIndex{1}\)) și calculăm probabilitatea de a găsi un electron pe fiecare coajă sferică. Reamintim că densitatea probabilității electronilor este cea mai mare la r = 0 (partea (b) din Figura \(\PageIndex{1}\)), deci densitatea punctelor este cea mai mare pentru cele mai mici cochilii sferice din partea (a) din Figura \(\PageIndex{1}\). În schimb, suprafața fiecărei cochilii sferice este egală cu 4nr2, care crește foarte rapid odată cu creșterea r (partea (C) din Figura \(\PageIndex{1}\)). Deoarece suprafața învelișurilor sferice crește mai rapid odată cu creșterea r decât scade densitatea probabilității electronilor, graficul probabilității radiale are un maxim la o anumită distanță (partea (d) din Figura \(\PageIndex{1}\)). Cel mai important, când r este foarte mic, suprafața unei cochilii sferice este atât de mică încât probabilitatea totală de a găsi un electron aproape de nucleu este foarte mică; la nucleu, probabilitatea electronilor dispare (partea (d) din Figura \(\PageIndex{1}\)).

pentru atomul de hidrogen, vârful în graficul de probabilitate radială are loc la r = 0,529 (52,9 pm), care este exact raza calculată de Bohr pentru orbita n = 1. Astfel, raza cea mai probabilă obținută din mecanica cuantică este identică cu raza calculată de mecanica clasică. Cu toate acestea, în modelul lui Bohr, electronul s-a presupus că se află la această distanță 100% din timp, în timp ce în mecanica cuantică Schr Modelul Xvdinger, este la această distanță doar o parte din timp. Diferența dintre cele două modele este atribuită comportamentului de undă al electronului și principiul incertitudinii Heisenberg.
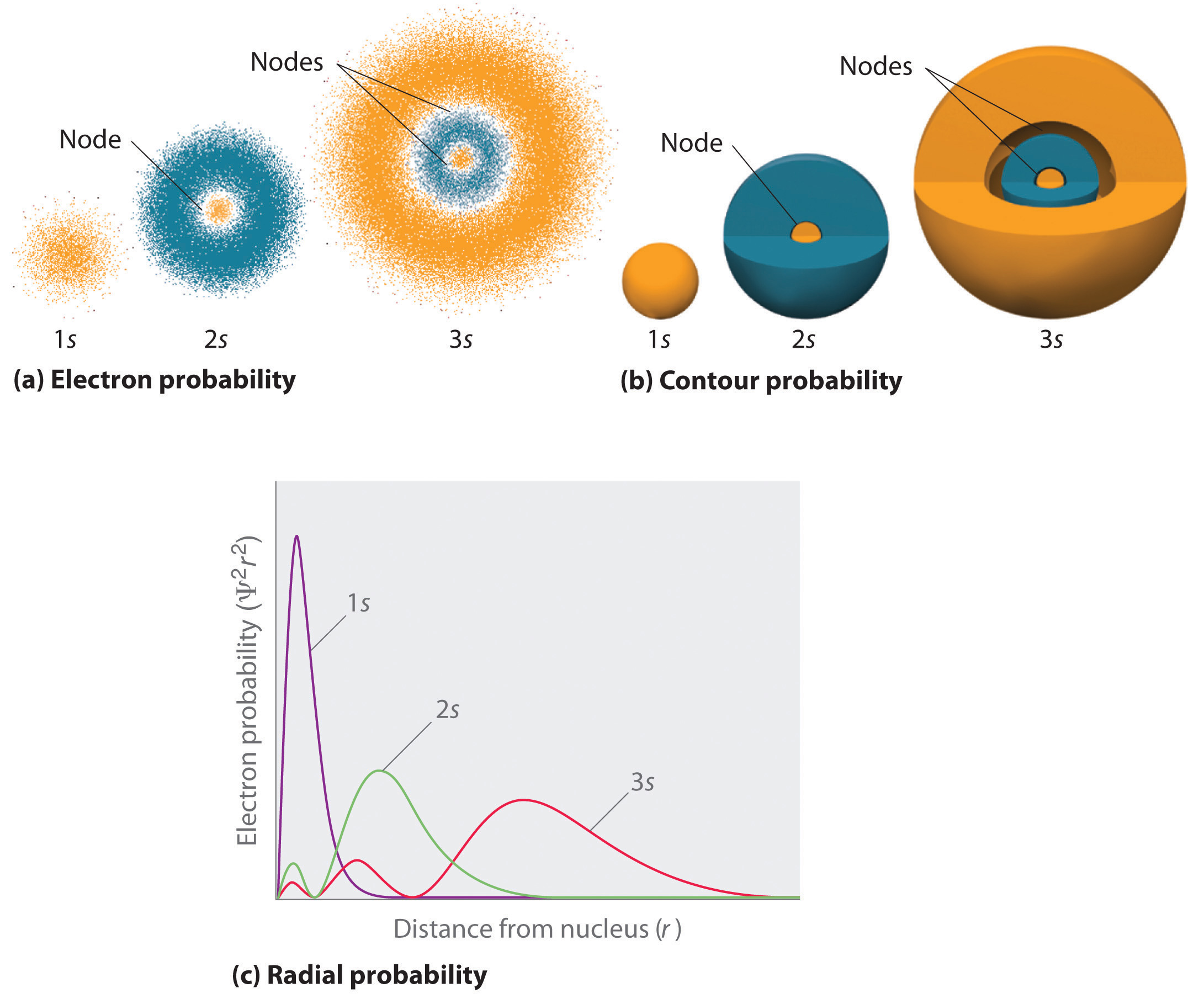
figura \(\PageIndex{2}\) compară densitățile probabilității electronilor pentru orbitalii hidrogenului 1s, 2s și 3s. Rețineți că toate cele trei sunt simetrice sferic. Cu toate acestea, pentru orbitalii 2S și 3s (și pentru toți ceilalți orbitali s), densitatea probabilității electronilor nu scade lin odată cu creșterea r. în schimb, o serie de minime și maxime sunt observate în graficele de probabilitate radială (partea (C) din Figura \(\PageIndex{2}\)). Minimele corespund nodurilor sferice (regiuni cu probabilitate de electroni zero), care alternează cu regiuni sferice cu probabilitate de electroni diferită de zero.