algumas coisas interessantes sobre ângulos e círculos.
- ângulo inscrito
- , Inscrito Ângulo de Teoremas
- Example: What is the size of Angle POQ? (O é o centro do círculo)
- Exemplo: Qual é o tamanho do Ângulo CBX?
- Ângulo em um Semicírculo (Thales Teorema)
- Outra Boa Razão pela Qual Ele Funciona
- exemplo: Qual é o tamanho do ângulo BAC?
- Localizar um Centro do Círculo
- Quadrilátero Cíclico
- Exemplo: Qual é o tamanho do Ângulo WXY?
ângulo inscrito
Em primeiro lugar, uma definição:
ângulo inscrito: um ângulo feito a partir de pontos sentados na circunferência do círculo.
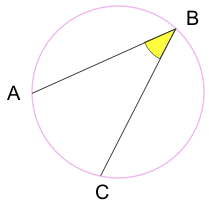
A e C são “pontos finais”
B é o “apex ponto”
Jogar com ele aqui:
Quando você mover ponto “B”, o que acontece com o ângulo?
, Inscrito Ângulo de Teoremas
Um ângulo inscrito numa° é a metade do ângulo central 2a°
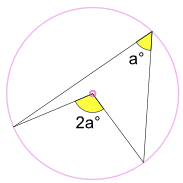
(Chamado de Ângulo no Centro Teorema)
E (mantendo os pontos de extremidade fixa) …
… o ângulo A° é sempre o mesmo, não importa onde esteja no mesmo arco entre os pontos finais:
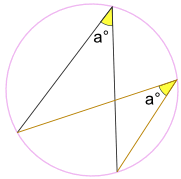
ângulo A° é o mesmo.
(Called the Angles Subtended by Same Arc Theorem)
Example: What is the size of Angle POQ? (O é o centro do círculo)
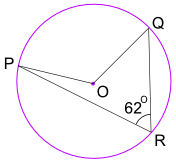
Ângulo POQ = 2 × Ângulo de PRQ = 2 × 62° = 124°
Exemplo: Qual é o tamanho do Ângulo CBX?
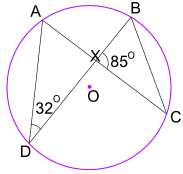
ângulo ADB = 32° Também é igual a Ângulo ACB.
E Angle ACB também é igual a Angle XCB.assim, no triângulo BXC conhecemos o ângulo BXC = 85°, e o ângulo XCB = 32°
agora usar ângulos de um triângulo adicionar a 180° :
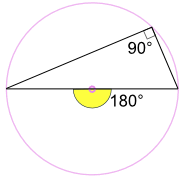
Ângulo em um Semicírculo (Thales Teorema)
Um ângulo inscrito em um círculo de diâmetro é sempre um ângulo reto:
(Os pontos finais são extremidades de um círculo de diâmetro,
o ápice ponto pode estar em qualquer lugar na circunferência.)
|
porquê? Porque: O inscrito ângulo de 90° é a metade do ângulo central 180° (Usando o “Ângulo no Centro Teorema” acima) |
 |
Outra Boa Razão pela Qual Ele Funciona
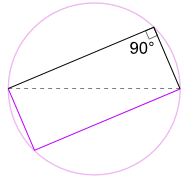
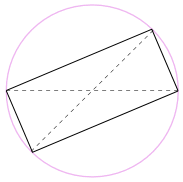
Nós também pode girar a forma em torno de 180° para fazer um rectângulo!
é um retângulo, porque todos os lados são paralelos, e ambas as diagonais são iguais.
E assim seus ângulos internos são todos ângulos retos (90°).
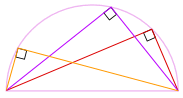
So there we go! Não importa onde esse ângulo está na circunferência, é sempre 90°
exemplo: Qual é o tamanho do ângulo BAC?
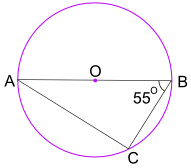
o ângulo no Teorema do semicírculo diz-nos que o ângulo ACB = 90°
usa agora ângulos de um triângulo adicionados a 180° para encontrar o ângulo BA:
Localizar um Centro do Círculo
podemos usar essa idéia para encontrar um centro do círculo:
- desenhar um ângulo reto a partir de qualquer ponto sobre a circunferência do círculo, desenhe o diâmetro, onde as duas pernas, bater o círculo
- fazer isso de novo, mas para um diâmetro diferente
, Onde os diâmetros cruz é o centro!
Quadrilátero Cíclico
|
Um “Cíclica” Quadrilátero tem cada vértice na circunferência do círculo: |
 |
|
Um Quadrilátero Cíclico é ângulos opostos adicionar a 180°:
|
 |
Exemplo: Qual é o tamanho do Ângulo WXY?
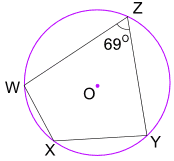
Opposite angles of a cyclic quadrilateral add to 180°

