Purplemath
Em matemática, uma “identidade” é uma equação que é sempre verdadeiro. Estes podem ser “trivialmente” verdadeiros, como” x = x “ou utilmente verdadeiros, como o teorema de Pitágoras” a2 + b2 = c2 ” para triângulos direitos. Existem muitas identidades trigonométricas, mas as seguintes são as que você mais provavelmente verá e usará.
Basic & Pythagorean, Angle-Sum & -Difference, Double-Angle, Half-Angle, Sum, Product
Content Continues Below
MathHelp.com
Need a custom math course?
K12 | College | Test Prep

Básico e Pitágoras de Identidades
Afiliado
Repare-se como um “co-(alguma coisa)”trigonometria proporção é sempre a recíproca de alguns “não-co” a relação. Você pode usar este fato para ajudá-lo a manter-se Direito que o cossecant vai com seno e secant vai com cosseno.
os seguintes (particularmente o primeiro dos Três abaixo) são chamados identidades “pitagóricas”.
sin2(t) + cos2(t) = 1
tan2(t) + 1 = sec2(t)
1 + cot2(t) = csc2(t)
Publicidade
Observe que as três identidades, acima de tudo, envolver quadrática e o número 1. Você pode ver claramente a relação pitagórica-aliom se você considerar o círculo unitário, onde o ângulo é t, o lado” oposto “é sin(t) = y, o lado” adjacente ” é cos(t) = x, e a hipotenusa é 1.
temos identidades adicionais relacionadas com o estado funcional da trigonometria razões:
sin(–t) = –sin(t)
cos(–t) = cos(t)
tan(–t) = –tan(t)
Observe que, em particular, que o seno e tangente são estranhas funções, sendo simétrica com relação à origem, enquanto que o co-seno é mesmo uma função, sendo simétrica sobre o eixo-y. O fato de que você pode levar o sinal “menos” do argumento para fora (para seno e tangente) ou eliminá-lo inteiramente (para cosseno) pode ser útil quando se trabalha com expressões complicadas.
Ângulo de Soma e Diferença de Identidades
sin(α + β) = sen(α) cos(β) + cos(α) sin(β)
sin(α – β) = sen(α) cos(β) – cos(α) sin(β)
cos(α + β) = cos(α) cos(β) – sin(α) sin(β)
cos(α – β) = cos(α) cos(β) + sin(α) sin(β)
By the way, no acima de identidades, os ângulos são indicados por letras gregas. A letra do tipo A, “α”, é chamada” alfa”, que é pronunciado”AL-fuh”. A letra do tipo b, “β”, é chamada” beta”, que é pronunciado”BAY-tuh”.
Conteúdo Continua Abaixo
clique duas vezes o Ângulo de Identidades
sin(2x) = 2 sin(x) cos(x)
cos(2x) = cos2(x) – sin2(x) = 1 – 2 sin2(x) = 2 cos2(x) – 1
Meio-Ângulo de Identidades
O acima identidades podem ser re-afirmado pelo quadrado de cada lado e dobrando todas as medidas angulares. Os resultados são os seguintes::
Affiliate

Sum Identities
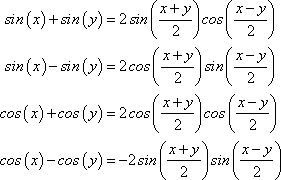
Product Identities
Afiliado
Você vai usar todas essas identidades, ou quase isso, para provar que o outro trigonométricas identidades e para a resolução de equações trigonométricas. No entanto, se você está indo para estudar cálculo, preste particular atenção para o seno e identidades coseno-semi-Ângulo restaurado, porque você vai usá-los muito em Cálculo integral.
URL: https://www.purplemath.com/modules/idents.htm