Esta secção cobre:
- Introdução a Funções definidas por partes
- Avaliação de Funções definidas por partes
- elaboração de Gráficos de Funções definidas por partes
- Como saber se Esta Função é Contínua ou Não-Contínua
- a Obtenção de Equações de Função por partes Gráficos
- Valor Absoluto como uma Função por partes
- Transformações de Funções definidas por partes
- Piecewise Função de Problemas do Word
- Mais Prática

de funções definidas por partes (ou peça-wise funções) são apenas o que elas são nomeadas: peças de diferentes funções (sub-funções) num único gráfico. A maneira mais fácil de pensar neles é se você desenhou mais de uma função em um grafo, e você simplesmente apagou partes das funções onde elas não deveriam estar (ao longo dos \(x\)’s); elas são definidas de forma diferente para diferentes intervalos de \(x\). \(y\) é definido de forma diferente para os diferentes valores de \(x\); Nós usamos o \(x\) para procurar em que intervalo ele está, para que possamos descobrir o que o \(y\) é suposto ser.
Note que existe um exemplo do Inverso de uma função de trechos aqui nos inversos da seção de funções.
Here’s an example and graph:
|
Piecewise Function |
Graph |
|
\(\displaystyle f\left( x \right)=\left\{ \begin{align}2x+8\,\,\,\,\,&\text{ if }x\le -2\\{{x}^{2}}\,\,\,\,\,\,\,\text{ }\,&\text{ if }x>-2\end{align} \right.\) (Existem outras formas de mostrar isto, como usar um “para” em vez de um “se”, e usar vírgulas ou semi-colões em vez do “se”.) Domínio: \(\mathbb{R}\,\,\,\text{ou}\,\,\left( {-\infty ,\infty } \right)\) Gama: \(\mathbb{R}\,\,\,\text{ou}\,\,\left( {-\infty ,\infty } \right)\) |
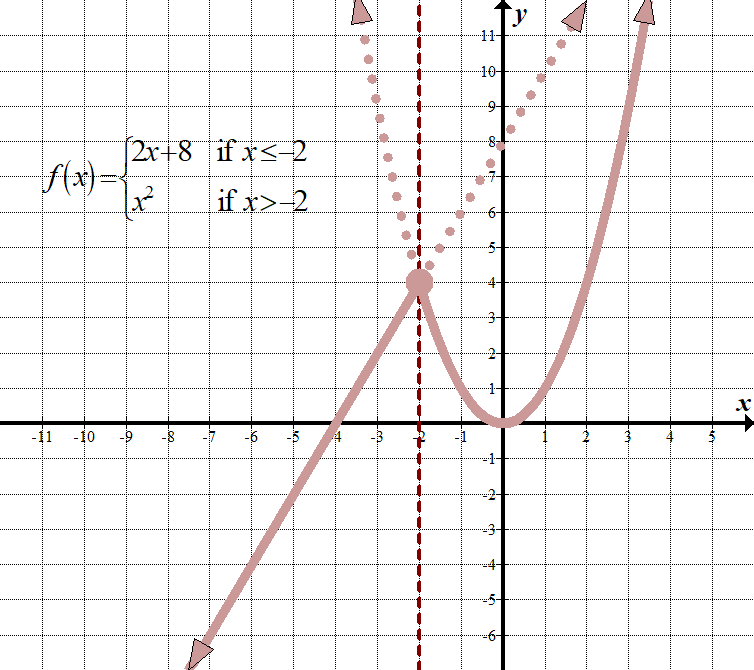 |
o Que isso significa para cada \(x\) menor ou igual a -2, temos o gráfico da linha \(2x+8\), como se fosse a única função no gráfico. Para cada valor \(x\) maior que -2, precisamos de graph \({{x}^{2}}}\), como se fosse a única função no gráfico. Então temos de “livrar-nos” das partes que não precisamos. Lembre-se que ainda usamos a origem como ponto de referência para ambos os gráficos!
veja como a linha vertical \(x=-2\) age como uma linha “limite” entre os dois grafos?
Note que o ponto \((-2,4)\) tem um círculo fechado sobre ele. Tecnicamente, ele só deve pertencer à função \(2x+8\), uma vez que essa função tem o sinal menor ou igual, mas como o ponto também está no grafo \({{x}^{2}}}\), podemos apenas usar um círculo fechado como se ele aparece em ambas as funções. Não é assim tão mau, pois não?
avaliar funções em trechos
por vezes, ser-lhe-ão dadas funções em trechos e ser-lhe-á pedido que as avalie; por outras palavras, Encontre os valores \(y\) quando lhe for dado um valor \(x\). Vamos fazer isto para \(x=-6\) e \(x=4\) (sem usar o gráfico). Aqui está novamente a função:
\(\displaystyle f\left( x \right)=\left\{ \begin{align}2x+8\,\,\,\,\,&\text{ se }x\le -2\\{{x}^{2}}\,\,\,\,\,\,\,\texto{ }\,&\text{ se }x>-2\end{align} \right.\)
primeiro queremos olhar para as condições à direita, para ver onde está o nosso \(x\). Quando \(x=-6\), sabemos que é menos de -2, por isso ligamos o nosso \(x\) a \(2x+8\) apenas. \(f (x)\) ou \(y\) é \((2)(-6)+8=-4\). Nós nem nos importamos com o \(\boldsymbol {{x}^{2}}\)! É assim tão fácil. Você também pode ver que fizemos isso corretamente usando o gráfico acima.
agora tente \(x=4\). Olhamos para a direita primeiro, e vemos que o nosso \(x\) é maior que -2, por isso ligamo-lo ao \({x}^{2}}\). (Podemos apenas ignorar o \(2x + 8\) desta vez.) \(f(x)\) ou \(y\) é \({{4}^{2}}=16\).
Graphing Piecewise Functions
provavelmente ser-lhe-á pedido para graph piecewise functions. Às vezes, os grafos contêm funções que são não-contínuas ou descontínuas, o que significa que você tem que pegar seu lápis no meio do grafo quando você está desenhando-o (como um salto!). Funções contínuas significa que você nunca tem que pegar seu lápis se você fosse atraí-los da esquerda para a direita.
e lembre-se que os gráficos são funções verdadeiras apenas se passarem no teste da linha Vertical.
vamos desenhar estas funções em trechos e determinar se elas são contínuas ou não-contínuas. Observe como desenhamos cada função como se fosse a única, e então “apagar” as partes que não são necessárias. Também teremos o domínio e o alcance como fizemos aqui na secção de funções algébricas.
| Piecewise Function | Graph |
|
\(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}-2x+8\,\,\,\,\,\,\text{if }x\le 4\\\frac{1}{2}x-2\,\,\,\,\,\,\,\,\,\text{if }x>4\end{array} \right.\) Continuous Domain: \(\mathbb{R},\,\,\,\text{or}\,\,\left( {-\infty ,\infty } \right)\) Range: \(\left( {0,\infty } \right)\) |
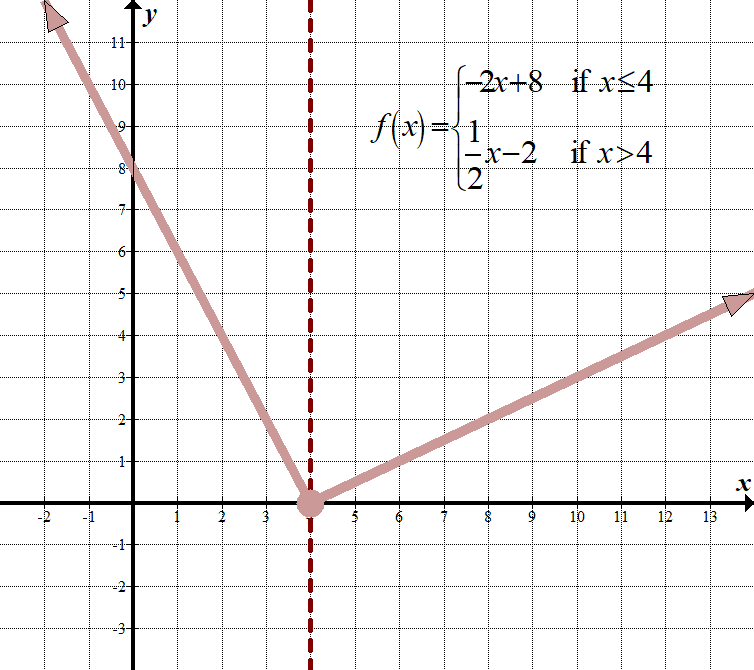 |
|
\(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}x+4\,\,\,\,\,\,\,\,\,\text{if }x<1\\2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{if 1}\le x<4\\x-5\,\,\,\,\,\,\,\,\,\text{if }x\ge 4\end{array} \right.\) Non-Continuous Domain: \(\mathbb{R},\,\,\,\text{or}\,\,\left( {-\infty ,\infty } \right)\) Range: \(\mathbb{R},\,\,\,\text{or}\,\,\left( {-\infty ,\infty } \right)\) |
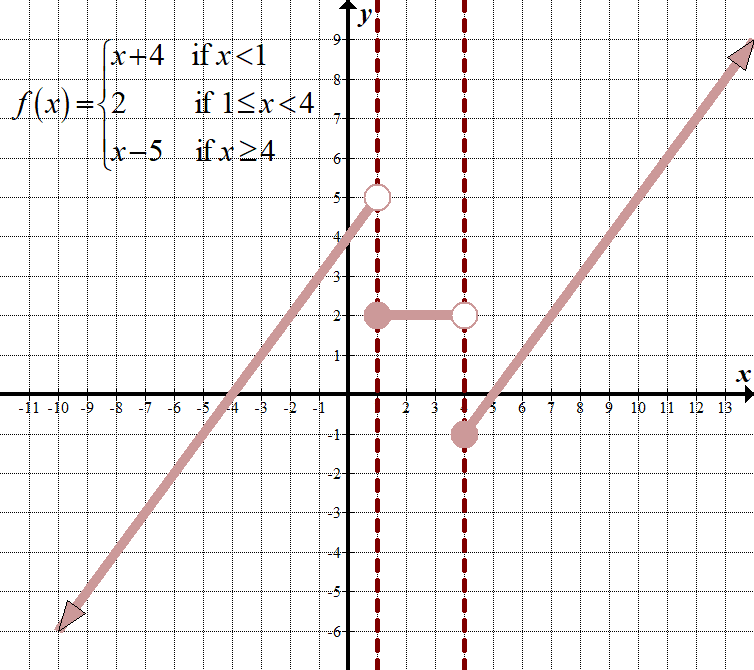 |
We can actually put piecewise functions in the graphing calculator:
| Piecewise Function Screens | Steps and Notes |
| Enter the piecewise function on three lines:
Aqui está o gráfico:
|
Para colocar o piecewise função \(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}x+4\,\,\,\,\,\,\,\,\,\text{se }x<1\\2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{se 1 }\le x<4\\-5+x\,\,\,\,\,\text{se }x\ge 4\end{array} \right.\ ) na calculadora, você pode inserir a função em três linhas dividindo a função em cada intervalo por uma “desigualdade de teste” desse intervalo (e assistir parêntesis!).
A razão dividimos por intervalos ou desigualdades é porque a calculadora irá retornar 1 se a desigualdade (tais como \(x<1\)) é verdadeira; por exemplo, \((x+4)\) só vai acabar \((x+4)/(1)\) quando \(x<1\). Quando \(x\ge 1\), estamos a dividir por 0, por isso nada será desenhado. Aqui está o que podemos colocar na calculadora: \(\displaystyle \begin{array}{l}{{Y}_{1}}=\left( {x+4} \right)/\left( {x<1} \right)\\{{Y}_{2}}=\left( 2 \right)/\left( {x\ge 1\text{ e }x<4} \right)\\{{Y}_{3}}=\left( {-5+x} \right)/\left( {x\ge 4} \right)\end{array}\) (Observe que você também pode fazer isso em uma linha multiplicando as condições, em vez de dividir, e usando sinais de adição entre cada uma das três funções/intervalos: \(\displaystyle {{Y}_{1}}=\left( {x+4} \right)\left( {x<1} \right)+\left( 2 \right)\left( {x\ge 1\text{ e }x<4} \right)+\left( {-5+x} \right)\left( {x\ge 4} \right)\).) Aqui estão as teclas para usar três linhas. Note que você usa a matemática 2 (teste) para chegar ao ecrã que tem o \(\le \), \(\ge \), e assim por diante. Por exemplo, 2nd MATH 6 recebe você \(\le \). Use 2nd MATH( TEST), right to LOGIC, then 1, for the “and” in \({{Y}_{2}}}\).
|
Como saber se Esta Função é Contínua ou Não-Contínua
Para saber se um piecewise gráfico é contínua ou não-contínua, você pode olhar para o limite de pontos e ver se o \(y\) o ponto é o mesmo em cada um deles. (Se os \(y\) ‘s fossem diferentes, haveria um “salto” no gráfico!)
vamos tentar isto para as funções que usamos acima:
| Piecewise Function | Check Boundary Points |
| \(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}-2x+8\,\,\,\,\,\,\,\text{if }x\le 4\\\frac{1}{2}x-2\,\,\,\,\,\,\,\,\,\,\text{if }x>4\end{array} \right.\) | Let’s check \(x=4\) in both parts of the function, since 4 is the “boundary point”:
\(\begin{array}{l}-2(4)+8=0\\\,\,\,\frac{1}{2}(4)-2=0\end{array}\) Desde que \(0=0\), este esta função é contínua. |
| \(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}x+4\,\,\,\,\,\,\,\,\,\,\,\,\,\text{se }x<1\\2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{se 1 }\le x<4\\-5+x\,\,\,\,\,\,\,\,\,\text{se }x\ge 4\end{array} \right.\) | vamos verificar nas duas primeiras partes da função. Nota na segunda parte, \(y\) é sempre 2:
\(\begin{array}{l}1+4=5\\\,\,\,\,\,\,\,\,\,2=2\end{array}\) Desde que \(5\ne 2\), podemos parar por aqui, e note que este esta função não é contínua. Se os \(y\) ‘ s fossem iguais, teríamos de ir um para verificar o próximo ponto de contorno em \(x=4\). |
a Obtenção de Equações de Função por partes Gráficos
Você pode ser solicitado a escrever uma função por partes, dado um gráfico. Agora que sabemos de que funções se trata, não é assim tão mau!
to review how to obtain equations from linear graphs, see Obtaining the Equations of a Line, and from quadratics, see Finding a Quadratic Equation from Points or a Graph.
Aqui estão os grafos, com explicações sobre como derivar suas equações em trechos:
| Piecewise Function Graph | Procedure to get Function |
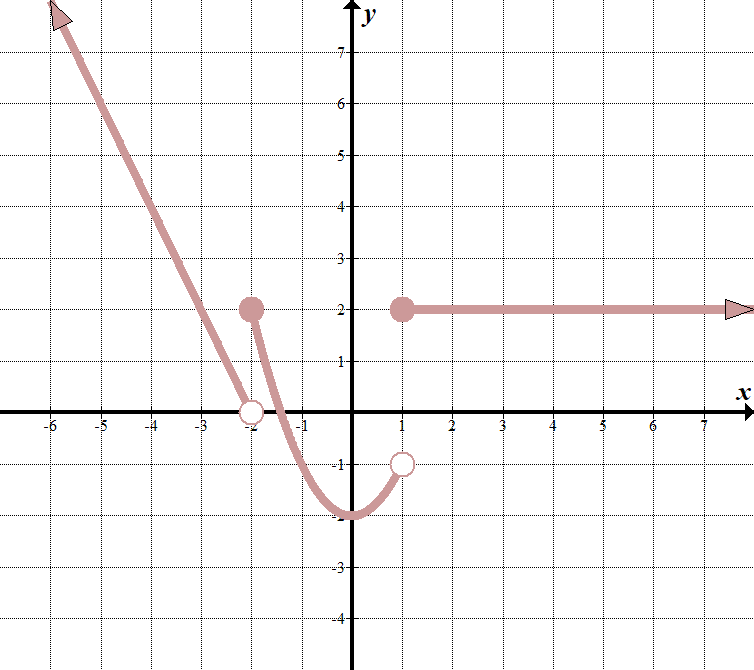 |
We see that our “boundary lines” are at \(x=-2\) and \(x=1\). We know that our function will look something like this (notice open and closed endpoints):
\(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}\text{ }……\,\,\,\,\,\,\,\,\text{se }x<-2\\\texto{ }……\,\,\,\,\,\,\,\,\text{se }-\text{2 }\le x<1\\\texto{ }……\,\,\,\,\,\,\,\,\text{se }x\ge 1\end{array} \right.\) Podemos escolher dois pontos \((-2,0)\) e \((-3,2)\) na linha mais à esquerda para obter a equação \(y=-2x-4\). a função do meio é \(y = {x}^{2}}-2\), e a função mais à direita é apenas a linha horizontal \(y=2\). assim, a função em trechos é: \(\displaystyle f\left( x \right)=\left\{ \begin{array}{l} 2x-4\,\,\,\,\,\,\,\text{se }x<-2\\\text{ }{{x}^{2}}-2\,\,\,\,\,\,\,\,\,\,\text{se }-\text{2}\le x<1\\\texto{ 2}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{se }x\ge 1\end{array} \right.\) |
 |
vemos que a nossa “linha de fronteira” é \(x=5\). Uma vez que as linhas se encontram em \((5,4)\), não importa onde colocamos o sinal \(\le \) ou \(\ge \) ; não podemos colocá-lo em ambos os lugares, ou não seria uma função. Temos até ao momento:
\(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}\text{ }……\,\,\,\,\,\,\,\,\,\text{se }x<5\\\texto{ }……\,\,\,\,\,\,\,\,\,\text{se }x\ge 5\end{array} \right.\) outra vez, temos de olhar para cada linha separadamente para determinar as suas equações. Podemos pegar 2 pontos de cada linha para obtê-los, ou derivar de encostas e \(y\) – interceptações; a função de trechos é: \(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}\frac{6}{5}x-2\,\,\,\,\,\,\,\text{se }x<5\\\frac{2}{5}x+2\,\,\,\,\,\,\,\text{se }x\ge 5\end{array} \right.\) |
Valor Absoluto como uma Função por partes
podemos escrever o valor absoluto funções como funções definidas por partes – é muito legal! Você pode querer rever a resolução de equações de valor absoluto e desigualdades antes de continuar a este tópico.
digamos que temos a função \(f\esquerda (x \Direita) = \Esquerda| x \direita/\). Pelo que aprendemos anteriormente, sabemos que quando \(x\) é positivo, uma vez que estamos tomando o valor absoluto, ele ainda será apenas \(x\). Mas quando \(x\) é negativo, quando tomamos o valor absoluto, temos que tomar o oposto (negá-lo), uma vez que o valor absoluto tem que ser positivo. Faz sentido? Então, por exemplo, se tivéssemos \(|5|\), pegaríamos apenas o que está dentro do sinal absoluto, uma vez que é positivo. Mas para \(|-5/\), temos que tomar o oposto (negativo) do que está dentro do valor absoluto para torná-lo \(\displaystyle 5\,\,\,(-\,-5=5)\).
isto significa que podemos escrever esta função de valor absoluto como uma função de trechos. Note que podemos obter o “ponto de viragem” ou “ponto de contorno” definindo o que estiver dentro do valor absoluto para 0. Então vamos usar a função original, ou negar a função, dependendo do sinal da função (sem o valor absoluto) nesse intervalo.
Por exemplo, podemos escrever \(\displaystyle \left| x \right|\text{ }=\left\{ \begin{array}{l}x\,\,\,\,\,\,\,\,\,\text{se }x\ge 0\\-x\,\,\,\,\,\text{se }x<0\end{array} \right.\). Note também que, se a função é contínua (não há “salto”) no ponto limite, não importa onde colocamos os sinais “menor ou igual a” (ou “maior ou igual a”), desde que não os repetamos! Não podemos repeti-los porque, teoricamente, não podemos ter dois valores de \(y\) para o mesmo \(x\), ou não teríamos uma função.
Here are more examples, with explanations. (You might want to review Quadratic Inequalities for the second example below):
| Absolute Value Function | Method to get Piecewise Function |
| \(g\left( x \right)=\left| {2x+3} \right|\) | Let’s first find the “boundary line”. Fazemos isto definindo o que está dentro do valor absoluto para 0, e depois resolvendo para \(\boldsymbol{x}\).
Quando \(2x+3\ge 0\), temos \(\displaystyle x\ge – \frac{3}{2}\) (Na verdade, podemos manter o \(\ge \) quando resolvemos). Quando \(2x+3\) é positivo, nós apenas tomamos “como está”, mas se é negativo, temos que negar a coisa toda. portanto, a função em trechos é: \(\displaystyle \left| {2x+3} \right|=\left\{ \begin{array}{l}2x+3\,\,\,\,\,\,\,\,\,\text{se }x\ge -\frac{3}{2}\text{ }\\-2x-3\,\,\,\,\,\text{se }x<-\frac{3}{2}\end{array} \right.\) Experimente-funciona! |
| \(f\left( x \right)=\left| {{{x}^{2}}-4} \right|\) | primeiro, Vamos encontrar a linha de limite(s)”; vamos definir o que está dentro de absoluto valor para 0.
When \({{x}^{2}}-4\ge 0\), we get \(x\le -2\) or \(x\ge 2\) (Tente alguns números!). Quando o \({{x}^{2} -4\) é positivo, nós apenas tomamos “como está”, mas se for negativo, temos que negá-lo. piecewise função é: \(\displaystyle \left| {{{x}^{2}}-4} \right|=\left\{ \begin{array}{l}, {{x}^{2}}-4\,\,\,\,\,\text{se }x\le -2\\4-{{x}^{2}}\,\,\,\,\,\text{se }-2<x<2\\{{x}^{2}}-4\,\,\,\,\,\text{se }x\ge 2\text{ }\end{array} \right.\) ou \(\displaystyle \left| {{{x}^{2}}-4} \right|=\left\{ \begin{array}{l}, {{x}^{2}}-4\,\,\,\,\,\,\text{se }x\le -2\text{ }\,\,\text{ou}\,\,\text{ }x\ge 2\\4-{{x}^{2}}\,\,\,\,\,\,\,\text{se }-2<x<2\end{array} \right.\) de Novo (uma vez que a função é contínua), ele realmente não importa onde temos o \(\le \) e \(\ge \) (em oposição a \(<\) e \(>\)), como tal não podemos repeti-los. |
| \(f\left( x \right)=2x+\left| {x+2} \right|\) | Este é um pouco mais complicado, pois temos um \(x\) dentro e fora do valor absoluto. Para a “linha limite”, nós só usamos o que está dentro do valor absoluto.
When \(x+2\ge 0\), we get \(x\ge -2\). Mas para a função de trechos, temos que usar toda a função, incluindo a parte que está fora do valor absoluto. Então, a função de trechos é: \(\displaystyle 2x+\left| {x+2} \right|=\left\{ \begin{array}{l}2x+x+2\,\,\,\,\,\text{se }x\ge -2\\2x-x-2\,\,\,\,\,\text{se }x<-2\end{array} \right.\) Vamos simplificar: \(\displaystyle 2x+\left| {x+2} \right|=\left\{ \begin{array}{l}3x+2\,\,\,\,\,\,\,\text{se }x\ge -2\\x-2\,\,\,\,\,\,\,\,\,\,\text{se }x<-2\end{array} \right.\) tente alguns valores inferiores e grandes então -2; eles devem funcionar! |
| \(g\left( x \right)=\left| {{{x}^{2}}-4x-5} \right|\) | Este é o melhor resolvidos com um sinal gráfico, pois temos uma quadrática e nós precisamos saber onde a função é positiva e negativa.
primeiro, factor quadrático dentro da função valor absoluto para \(\esquerda ({x-5} \direita)\esquerda ({x+1} \direita)\). Então use um gráfico de sinais para ver onde os fatores são positivos e negativos, e lembre-se que onde os fatores são positivos, nós usamos a função “como está”, e onde os fatores são negativos, Nós negamos a função: \(\displaystyle \left| {{{x}^{2}}-4x-5} \right|=\left\{ \begin{array}{l}, {{x}^{2}} 4x-5\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{se }x\le -1\,\,\,\,\texto{ou}\,\,\,\,x\ge 5\\-\left( {{{x}^{2}}-4x-5} \right)\,\,\,\,\text{se }-1<x<5\text{ }\end{array} \right.\) |
| \(\displaystyle g\left( x \right)=\frac{{\left| {x+2} \right|}}{{x+2}}\) | Esta é uma função racional, já que não há uma variável no denominador.
When \(x+2\ge 0\), we get \(\displaystyle x\ge -2\). Quando \(x+2\) é positivo, nós apenas tomá-lo “como é”, mas se é negativo, temos que negar que o valor absoluto: \(\displaystyle \frac{{\left| {x+2} \right|}}{{x+2}}=\left\{ \begin{array}{l}\frac{{x+2}}{{x+2}}\,\,\,\,\,\,\,\,\,\text{se }x\ge -2\\\frac {{x-2}}{{x+2}}\,\,\,\,\,\,\text{se }x<-2\end{array} \right.\). Mas temos que ter cuidado, já que \(x\ne 2\) (restrição de domínio: o denominador seria 0). portanto, a função em trechos é: \(\displaystyle \frac{{\left| {x+2} \right|}}{{x+2}}=\left\{ \begin{array}{l}1\,\,\,\,\,\,\,\,\,\,\text{se }x>-2\\-1\,\,\,\,\,\,\text{se }x<-2\end{array} \right.\). |
Pode também ser-lhe pedido que pegue num gráfico de valor absoluto e o escreva como uma função em trechos:
| Absolute Value Graph | Method to get Piecewise Function |
 |
We see that our “boundary line” is at \(x=0\), so what’s inside the absolute value sign must be \(x\) or a factor of \(x\). (Isto é porque para obter a linha de contorno com uma função de valor absoluto, definimos o que está dentro do valor absoluto para 0, e resolvemos para \(x\)).
When \(x >0\), we can see that the equation of the line is \(y=2x-2\). Quando \(x <0\), a equação é \(y=2x-2\). Podemos escrever isso como uma função por partes: \(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}2x-2\,\,\,\,\,\,\,\text{se }x>0\\-2x-2\,\,\,\text{se }x\le 0\end{array} \right.\) também podemos escrever isto como uma função de valor absoluto transformada: \(y=2\esquerda| x \direita|-2\) ou \(y=\esquerda| {2x} \direita|-2\) (dado que o 2 é positivo, pode estar dentro ou fora do \(\esquerda| {\,\,} \direita|\)). (Isto faz sentido, pois quando o que está dentro de \(\left| {\,\,} \right|\) é \(> 0\), podemos usar a função normal \(y=2x-2\), e quando o que está dentro é \(< 0\), podemos negar o valor absoluto parte para torná-lo \(y=\left( {2x} \right)-2\)). |
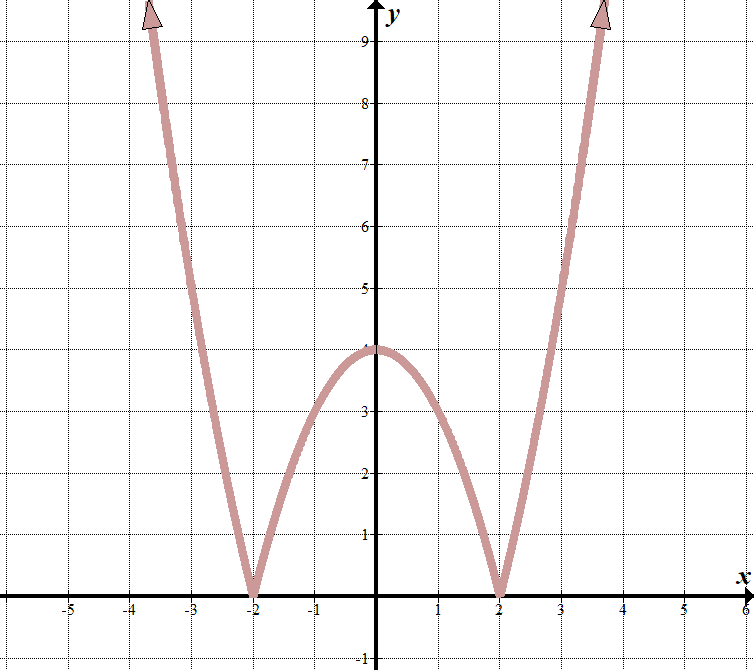 |
Nós vemos que o nosso “limite de linhas” estão em \(x=2\) e \(x=-2\), então o que está dentro do valor absoluto do sinal deve ter fatores de \(x-2\) e \(x+2\).
Quando \(x<-2\) ou \(x>2\), podemos ver que o gráfico se parece com a parte normal do gráfico \(y={{x}^{2}}-4\). (Eu descobri isso conhecendo os fatores, e tendo um bom palpite!) Quando \(-2<x<2\), a equação é invertida, ou negada (capotou o \(x\)-eixo). Podemos escrever isso como uma função por partes: \(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}, {{x}^{2}}-4\,\,\,\,\,\,\,\,\,\text{se }x<-2\text{ ou }x>2\\-{{x}^{2}}\text{+ 4}\,\,\,\,\,\,\text{se }-2\le x\le 2\end{array} \right.\) Podemos ver que isto iniciou uma função quadrática transformada \(y={{x}^{2}}-4\) com um valor absoluto à sua volta, dado que todos os valores \(y\) são positivos: \(y=\left| {{{x}^{2}}-4} \right|\). |
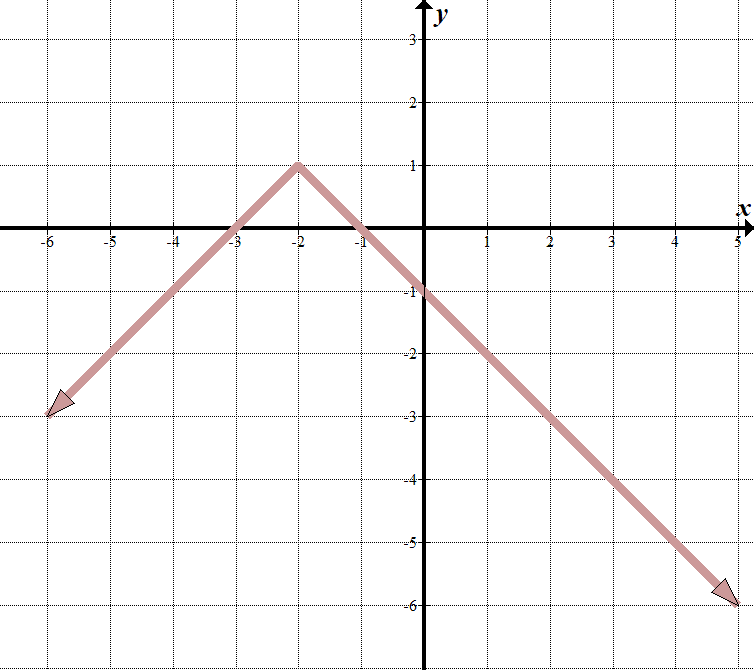 |
vemos que a nossa “linha de fronteira” é \(x=-2\), então o que está dentro do valor absoluto do sinal deve ser \(x+2\).
When \(x >-2\), we can see that the equation of the line is \(y=-x-1\). Quando \(x <-2\), a linha é \(y=x+3\). Podemos escrever isso como uma função por partes: \(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}-x-1\,\,\,\,\,\,\text{se }x>-2\\x+3\,\,\,\,\,\,\,\,\,\,\text{se }x\le -2\end{array} \right.\) é provavelmente mais fácil escrever isto como uma função de valor absoluto transformada. Podemos ver que a função de valor absoluto pai é invertida verticalmente, mover para a esquerda 2, e para cima 1. A nossa equação de valor absoluto é \(y= – \left / {x+2} \right|\,\,+\,\,1\). Isto é o mesmo que a função de trechos acima. Tenta-funciona! |
Transformações de Funções definidas por partes
Vamos fazer uma transformação de uma função por partes. Nós aprendemos como sobre as funções dos pais e suas transformações aqui na seção de gráficos e transformações dos pais. Você provavelmente vai querer ler esta seção primeiro, antes de tentar uma transformação em trechos.
vamos transformar a seguinte função em trechos invertida em torno do eixo \(x\), verticalmente esticada por um fator de 2 unidades, 1 unidade para a direita, e 3 unidades para cima.
Vamos desenhar \(-2f\left( x-1 \right)+3\), onde:
\(\displaystyle f\left( x \right)=\left\{ \begin{align}x+4\,\,\,\,\,\,\,\,&\text{ se }x<&\text{ se 1 }\le x<4\\x-5\,\,\,\,\,\,\,\,&\text{ se }x\ge 4\end{align} \right.\)
vamos certificar-nos de que usamos os pontos “limite” quando preenchermos o gráfico-t para a transformação. Lembre-se que as transformações dentro dos parêntesis são feitas no \(x\) (fazendo a matemática oposta), e no exterior são feitas no \(y\). Para chegar a um gráfico-t, como mostrado na tabela abaixo, podemos usar pontos chave, incluindo dois pontos em cada uma das”linhas de contorno”.
Note que como esta transformação é complicada, podemos chegar a uma nova função em trechos, transformando as 3 ” peças “e também transformando os”\(x\) “S onde os pontos de contorno estão (adicionando 1, ou indo para a direita 1), uma vez que fazemos a matemática oposta para OS”\(x\) ” s. Para obter as novas funções em cada intervalo, podemos apenas substituir ” \(x-1\) “por” \(x\) ” na equação original, multiplicar por -2 e, em seguida, adicionar 3. Por exemplo, \(\displaystyle -2f\left( {x-1} \right)+3=-2\left+3=-2\left( {x+3} \right)+3=-2x-3\).
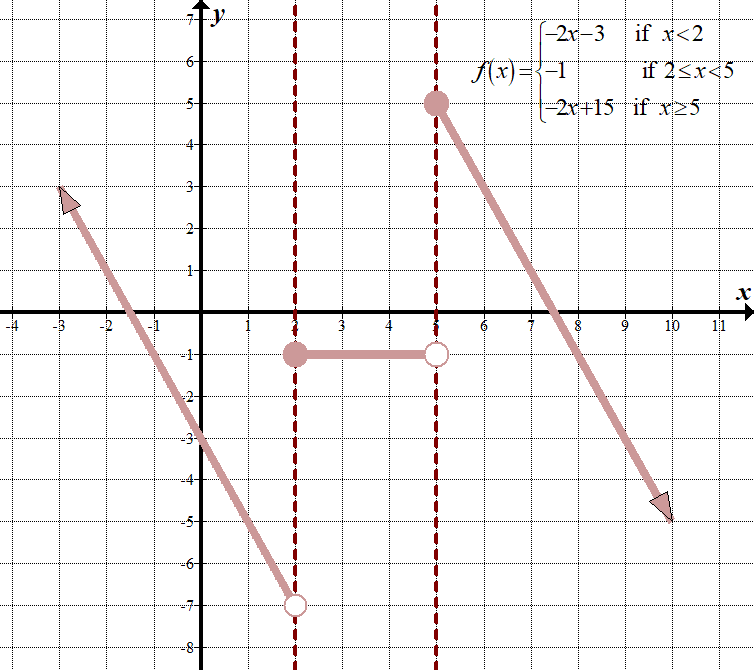
\(\displaystyle -2f\left( {x-1} \right)+3=\left\{ \begin{array}{l}-2\left( {\left( {x-1} \right)+4} \right)+3=-2x-3,\,\,\,\,\text{ se }x-1<1\,\,\,\left( {x<2} \right)\\-2\left( 2 \right)+3=-1,\,\,\,\,\text{ se }\,\text{ 2 }\le x<5\\-2\left( {\left( {x-1} \right)-5} \right)+3=-2x+15,\,\,\,\,\text{ se }x\ge 5\end{array} \right.\)
Aqui estão os gráficos “antes” e “depois”, incluindo o gráfico t:
| Piecewise Parent Function | T-chart | Transformation of Function | ||||||||||||||||||||||||||||||||||||||||
| \(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}x+4\,\,\,\,\,\,\,\,\text{if }x<1\\2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{if 1 }\le x<4\\x-5\,\,\,\,\,\,\,\,\text{if }x\ge 4\end{array} \right.\)
|
|
\(\displaystyle -2f\left( {x-1} \right)+3=\left\{ \begin{array}{l}-2x-3\,\,\,\,\,\,\,\,\,\text{if }x<2\\-1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{if 2}\le x<5\\-2x+15\,\,\,\,\,\,\text{if }x\ge 5\end{array} \right.\)
|
||||||||||||||||||||||||||||||||||||||||
Piecewise Function Word Problems
 Problem:
Problem:
seu favorito groomer do cão cargas de acordo com o peso do seu cão. Se o seu cão tem 15 libras e menos, o groomer cobra 35 dólares. Se o seu cão tem entre 15 e 40 libras, ela cobra 40 dólares. Se o seu cão tiver mais de 40 libras, ela cobra 40 dólares, mais 2 dólares adicionais por cada libra.
(a) escrever uma função em trechos que descreve o que o seu groomer do cão cobra.
(B) grafo a função.
(c) qual seria a taxa de groomer se o seu cão bonito pesa 60 libras?solução:(a) vemos que os “pontos limite” são 15 e 40, uma vez que estes são os pesos onde os preços mudam. Uma vez que temos dois pontos de fronteira, teremos três equações na nossa função de trechos. Temos de começar por 0, já que os cães têm de pesar mais de 3 kg.:
\(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}\text{ }……\,\,\,\,\,\,\,\,\,\text{se }0<x\le 15\\\texto{ }……\,\,\,\,\,\,\,\,\,\text{se }15<x\le 40\\\texto{ }……\,\,\,\,\,\,\,\,\,\text{se }x>40\end{array} \right.\)
estamos à procura das ” respostas “(quanto os custos de aliciamento) para as” perguntas ” (quanto pesa o cão) para as três gamas de preços. Os dois primeiros são apenas taxas fixas ($35 e $ 40, respectivamente). A última equação é um pouco mais complicada; o groomer cobra $ 40 mais $2 por cada libra acima de 40. Vamos tentar números reais: se o seu cão pesa 60 libras, ela vai cobrar $40 mais $2 vezes \(20(60-40)\). Vamos transformar isso em uma equação: \(40+2 (x–40)\), que simplifica para \(2x-40\) (veja como 2 é o declive?).
toda a função em trechos é:
\(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}\text{ }35\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{se }0<x\le 15\\\texto{ }40\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{se }15<x\le 40\\\text{ }40+2\left( {x-40} \right)\,\,\,\,\,\,\text{se }x>40\end{array} \right.\) ou \(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}\text{ }35\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{se }0<x\le 15\\\texto{ }40\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{se }15<x\le 40\\\text{ }2x-40\,\,\,\,\,\,\,\text{se }x>40\end{array} \right.\)
(b) Let’s graph: Note that this piecewise equation is non-continuous. Note também que um domínio razoável para este problema pode ser \(\esquerda ({0,200} \direita]\) (dado cães não pesam mais de 200 libras!) e um intervalo razoável pode ser \(\left \ cup \left\).
Note that this piecewise equation is non-continuous. Note também que um domínio razoável para este problema pode ser \(\esquerda ({0,200} \direita]\) (dado cães não pesam mais de 200 libras!) e um intervalo razoável pode ser \(\left \ cup \left\).
(C) Se o seu cão pesa 60 libras, podemos usar o gráfico, ou a função para ver que você teria que pagar $80. Whoa! Isso custa mais do que um corte de cabelo humano (pelo menos Os meus cortes de cabelo)!problema: planeias vender-lhe t-shirts de matemática como angariação de fundos. A empresa de T-shirts cobra 10 dólares por camisa pelas primeiras 75 camisas. Após os primeiros 75 camisas que você compra até 150 Camisas, a empresa vai baixar o seu preço para US $7,50 por camisa. Depois de comprar 150 Camisas, o preço vai diminuir para US $5 por camisa. Escreva uma função que modele esta situação.
solução:
vemos que os “pontos limite” são 75 e 150, uma vez que estes são o número de T-shirts comprados onde os preços mudam. Uma vez que temos dois pontos de fronteira, teremos três equações na nossa função de trechos. Vamos começar com \(x\ge 1\), uma vez que, assumimos que pelo menos uma camisa é comprada. Note neste problema, o número de T-shirts compradas (\(x\)), ou o domínio, deve ser um inteiro, mas esta restrição não deve afetar o resultado do problema.
\(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}\text{ }……\text{ se }1\le x\le 75\\\text{ }……\text{ se }75<x\le 150\\\text{ }……\text{ se }x>150\end{array} \right.\)
estamos à procura das “respostas” (custo total das t-shirts) para as “perguntas” (Quantas são compradas) para as três gamas de preços.
para até e incluindo 75 Camisas, o preço é de $10, de modo que o preço total seria \(10x\). Para mais de 75 camisas, mas até 100 Camisas, o custo é de US $7,50, mas os primeiros 75 T-shirts ainda vai custar US $10 por camisa. A segunda função inclui os $ 750 gastos nas primeiras 75 camisas (75 vezes $10), e também inclui $7,50 vezes o número de camisas acima de 75, que seria \((x-75)\). Por exemplo, se você comprou 80 Camisas, você teria que gastar \(\$10\vezes 75=\$750\), mais \(\$7,50\vezes 5\,\) (80 – 75) para as camisas depois da camisa 75.
Similarly, for over 150 shirts, we would still pay the $10 price up through 75 shirts, the $7.50 preços para 76 a 150 camisas (mais 75 Camisas), e então $5 por camisa para o número de camisas compradas mais de 150. Nós pagamos.\(10(75)+7.50(75)+5( x-150)\) para camisas \(x\). Põe números e tenta!
toda esta função é:
\(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}\text{ }10x\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{se }1\le x\le 75\\\text{ }7,5 x\text{ }+\texto{ }187.5\,\,\,\,\,\texto{7}5<x\le 150\\\text{ }5x+562.5\,\,\,\,\,\,\,\,\,\,\text{ if }x>150\end{array} \right.\) ou \(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}\text{ }10x\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{se }1\le x\le 75\\\text{ }7,5 x\text{ }+\texto{ }187.5\,\,\,\,\,\texto{7}5<x\le 150\\\text{ }5x+562.5\,\,\,\,\,\,\,\,\,\,\,\text{se }x>150\end{array} \right.problema: um serviço de autocarro custa 50 dólares para as primeiras 400 milhas, e cada 300 milhas adicionais (ou uma fracção delas) adiciona 10 dólares à tarifa.
Use uma função em trechos para representar a tarifa de ônibus em termos de distância em milhas.
solução:
Este é realmente um problema complicado, mas vamos primeiro pensar sobre o “ponto limite”, que é 400. É bastante simples quando o passeio é menos de 400 Milhas; o custo é de US $ 50.
Por mais de 400 milhas, temos que subtrair as primeiras 400 milhas (mas lembre-se de incluir os primeiros $50), dividir o número de milhas à esquerda por 300 milhas (e arredondar, se houver uma quantia fracionada), e multiplicar isso por $10.
A parte complicada é quando nós “arredondar” para uma porção dos próximos 300 milhas. Podemos usar uma função de “tecto” (designada por \(\esquerda\lceil {} \direita\rceil \)); esta função dá o número menos inteiro que é maior ou igual à sua entrada; por exemplo, o tecto de 3.5 e 4 é 4.assim, isto é o que temos:
\(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}\text{ }o 50\texto{ }\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{se }0\le x\le 400\\\text{ }50+10\times \left\lceil {\frac{{x-400}}{{300}}} \direito\rceil \texto{ }\,\,\,\,\,\,\text{ se }x>400\end{array} \right.\)
vamos tentar! Se tivermos um passeio de 1500 milhas, o custo seria \(\displaystyle 50+10\vezes \esquerda \ lceil {\frac{{1500-400}}{{300}}} \direita\rceil \text { } = 50+10\vezes 4 = \ $ 90\).problema:
Que valor de \(\boldsymbol{a}\) tornaria esta função em trechos contínua?
\(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}3{{x}^{2}}+4\,\,\,\,\,\text{ se }x<-2\\5x+\boldsymbol{um}\,\,\,\,\,\,\,\,\text{se }x\ge -2\end{array} \right.\)
solução:
para a função em trechos ser contínua, no ponto limite (onde a função muda), os dois valores \(y\) devem ser os mesmos. Podemos plug em -2 para \(x\) em ambas as funções e certifique-se de que o \(y\)’s são os mesmos
\(\begin{align}3{{x}^{2}}+4&=5x+a\\3{{\left( {-2} \right)}^{2}}+4&=5\left( {-2} \right)+a\\12+4&=-10+a\\&=26\end{align}\)
Se \(a=26\), o piecewise função é contínua! aprenda estas regras, e pratique, pratique, pratique!
Mais prática: Use o elemento Mathway abaixo para tentar escrever uma função em trechos. Carregue no Submit (a seta azul à direita do problema) e carregue em escrever o valor absoluto em trechos para ver a resposta.
Você também pode digitar em seu próprio problema, ou clique nos três pontos no canto superior direito e clique em “exemplos” para perfurar por tópico.
Se você clicar em Tap para ver os passos, ou clique aqui, você pode se registrar na Mathway para um teste gratuito, e então atualizar para uma assinatura paga a qualquer momento (para obter qualquer tipo de problema matemático resolvido!).
sobre Matrizes e sistemas de resolução com matrizes-você está pronto!