- Objetivos
- trabalho feito contra a gravidade
- Using Potential Energy to Simplify Calculations
- exemplo 1. A força para parar de cair
- estratégia
- Solution
- Discussão
- Exemplo 2. Encontrar a velocidade de uma montanha-russa a partir de sua altura
- estratégia
- solução para a parte 1
- Solução para a Parte 2
- discussão e implicações
- Making Connections: Take-Home Investigation-Converting Potential to Kinetic Energy
- Resumo da secção
- Questões Conceituais
- Problemas & Exercícios
- Glossário
- Selecionado Soluções para os Problemas & Exercícios
Objetivos
Ao final desta seção, você será capaz de:
- Explique energia potencial gravitacional em termos de trabalho realizado contra a gravidade.
- mostra que a energia potencial gravitacional de um objeto de massa M à altura h na terra é dada por PEg = mgh.
- mostra como o conhecimento da energia potencial em função da posição pode ser usado para simplificar cálculos e explicar fenômenos físicos.
trabalho feito contra a gravidade
subir escadas e levantar objetos é trabalho no sentido científico e cotidiano—é trabalho feito contra a força gravitacional. Quando há trabalho, há uma transformação de energia. O trabalho feito contra a força gravitacional vai para uma forma importante de energia armazenada que vamos explorar nesta seção.

Figura 1. (a) o trabalho feito para levantar o peso é armazenado no sistema massa-Terra como energia potencial gravitacional. b) à medida que o peso se move para baixo, esta energia potencial gravitacional é transferida para o relógio de cuco.
vamos calcular o trabalho feito na elevação de um objeto de massa M através de uma altura h, como Na Figura 1. Se o objecto for elevado a uma velocidade constante, a força necessária para o levantar é igual à sua mg de peso. O trabalho feito na massa é então W = Fd = mgh. Nós definimos isto como sendo a energia potencial gravitacional (PEg) colocada no sistema objeto-Terra. Esta energia está associada ao estado de separação entre dois objetos que se atraem pela força gravitacional. Por conveniência, nós nos referimos a isto como o PEg ganho pelo objeto, reconhecendo que isto é energia armazenada no campo gravitacional da Terra. Por que usamos a palavra “sistema”? A energia potencial é uma propriedade de um sistema e não de um único objeto—devido à sua posição física. O potencial gravitacional de um objeto é devido à sua posição em relação ao entorno dentro do sistema Terra-objeto. A força aplicada ao objeto é uma força externa, de fora do sistema. Quando faz um trabalho positivo, aumenta a energia potencial gravitacional do sistema. Como a energia potencial gravitacional depende da posição relativa, precisamos de um nível de referência para definir a energia potencial igual a 0. Normalmente escolhemos este ponto para ser a superfície da Terra, mas este ponto é arbitrário; o que é importante é a diferença na energia potencial gravitacional, porque esta diferença é o que se relaciona com o trabalho feito. A diferença na energia potencial gravitacional de um objeto (no sistema Terra-objeto) entre dois degraus de uma escada será a mesma para os dois primeiros degraus como para os dois últimos degraus.a conversão entre energia potencial e energia cinética pode ser convertida para outras formas de energia, como a energia cinética. Se liberarmos a massa, a força gravitacional fará uma quantidade de trabalho igual a mgh sobre ela, aumentando assim a sua energia cinética por essa mesma quantidade (pelo teorema da energia de trabalho). Vamos achar mais útil considerar apenas a conversão de PEg para KE sem considerar explicitamente o passo intermediário do trabalho. (Ver Exemplo 2. Este atalho torna mais fácil resolver problemas usando energia (se possível) em vez de usar explicitamente forças.
mais precisamente, definimos a mudança na energia potencial gravitacional ΔPEg como ΔPEg = mgh, onde, para simplicidade, denotamos a mudança na altura por h em vez da Δh habitual. Note que h é positivo quando a altura final é maior que a altura inicial, e vice-versa. Por exemplo, se uma massa de 0,500 kg pendurada de um relógio de cuco é levantada 1.00 m, então a sua mudança na energia potencial gravitacional é
\begin{array}{lll}mgh&&(0.500\text{ kg})(9.80\text{ m/s}^2)(1.00\text{ m})\\\text{ }&&4.90\text{ kg}\cdot\text{m}^2\text{/s}^2=4.90\text{ J}\end{array}\\
Observe que as unidades de energia potencial gravitacional vir a ser joules, o mesmo que para o trabalho e outras formas de energia. À medida que o relógio corre, a massa é baixada. Podemos pensar na massa como desistindo gradualmente dos seus 4.90 J de energia potencial gravitacional, sem considerar diretamente a força da gravidade que faz o trabalho.
Using Potential Energy to Simplify Calculations

Figura 2. A mudança na energia potencial gravitacional (ΔPEg) entre os pontos A E B é independente do caminho.
a equação ΔPEg = mgh aplica-se a qualquer caminho que tenha uma alteração na altura de h, não apenas quando a massa é elevada para cima. (Ver Figura 2.) É muito mais fácil calcular mgh (uma multiplicação simples) do que calcular o trabalho feito ao longo de um caminho complicado. A ideia de energia potencial gravitacional tem a dupla vantagem de ser amplamente aplicável e de facilitar os cálculos.
a Partir de agora, vamos considerar que qualquer mudança na posição vertical h de uma massa m é acompanhada por uma mudança na energia potencial gravitacional mgh, e vamos evitar o equivalente, mas mais difícil a tarefa de calcular o trabalho realizado por ou contra a força gravitacional.
ΔPEg = mgh para qualquer caminho entre os dois pontos. A gravidade é uma de uma pequena classe de forças onde o trabalho feito pela força ou contra a força depende apenas dos pontos de partida e de chegada, e não do caminho entre elas.
exemplo 1. A força para parar de cair
a 60.Uma pessoa de 0 kg salta para o chão a partir de uma altura de 3,00 m. Se ele cair de forma rígida (com suas articulações do joelho comprimindo em 0,500 cm), calcule a força nas articulações do joelho.
estratégia
a energia desta pessoa é reduzida a zero nesta situação pelo trabalho que lhe é feito pelo chão à medida que pára. O PEg inicial é transformado em KE quando ele cai. O trabalho feito pelo chão reduz esta energia cinética a zero.
Solution
the work done on the person by the floor as he stops is given by W = Fd cos θ = −Fd, with a minus sign because the displacement while stopping and the force from floor are in opposite directions (cos θ = cos 180 ° = -1). O chão remove energia do sistema, por isso faz um trabalho negativo.
a energia cinética que a pessoa tem ao chegar ao chão é a quantidade de energia potencial perdida ao cair através da altura h: KE = – ΔPEg = – mgh.
a distância d que os joelhos da pessoa dobram é muito menor do que a altura h da queda, de modo que a mudança adicional na energia potencial gravitacional durante a curva do joelho é ignorada.
O trabalho feito pelo chão sobre a pessoa pára a pessoa e leva a energia cinética da pessoa a zero: W = −KE = mgh.
combinando esta equação com a expressão para W dá −Fd = mgh.
recordando que h é negativo porque a pessoa caiu, a força nas articulações do joelho é dada por
\displaystyle{F}=-\frac{mgh}{d}=-\frac{\left(60.0\text{ kg}\right)\left(9.80\text{ m/s}^2\right)\left(-3.00\text{ m}\right)}{5.00\times10^{-3}\text{ m}}=3.53\times10^5\text{ N}\\
Discussão
uma grande força (500 vezes mais do que a de uma pessoa de peso) sobre o impacto de curto tempo é o suficiente para quebrar os ossos. Uma maneira muito melhor de amortecer o choque é dobrando as pernas ou rolando no chão, aumentando o tempo em que a força atua. Um movimento de flexão de 0,5 m desta forma produz uma força 100 vezes menor do que no exemplo. O salto de um canguru mostra este método em ação. O canguru é o único grande animal a usar saltos para locomoção, mas o choque em hopping é amortecido pela flexão de suas patas traseiras em cada salto. (Ver Figura 3.)

Figura 3. O trabalho feito pelo solo sobre o canguru reduz sua energia cinética a zero à medida que aterra. No entanto, aplicando a força do solo nas patas traseiras a uma distância mais longa, o impacto nos ossos é reduzido. (crédito: Chris Samuel, Flickr)
Exemplo 2. Encontrar a velocidade de uma montanha-russa a partir de sua altura
- Qual é a velocidade final da montanha-russa mostrada na Figura 4 se ela começa do repouso no topo da colina 20,0 m e o trabalho feito por forças de fricção é negligenciável?
- Qual é a sua velocidade final (assumindo novamente fricção negligenciável) se a sua velocidade inicial for 5.00 m/s?
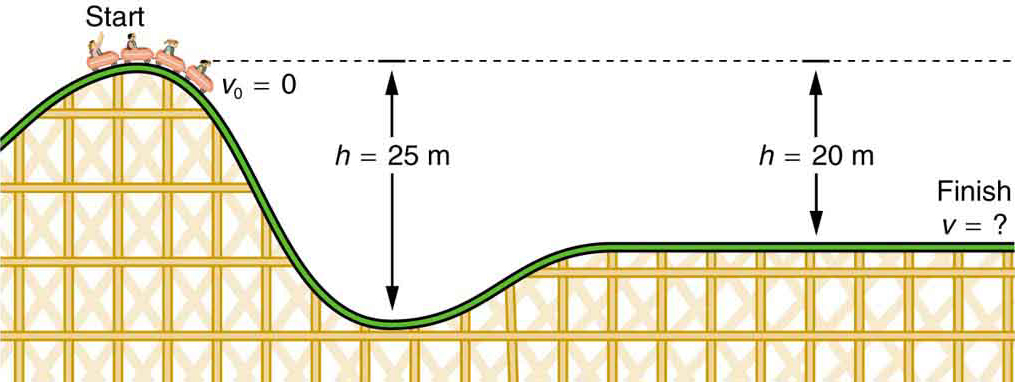
Figura 4. A velocidade de uma montanha-russa aumenta à medida que a gravidade a puxa para baixo e é maior no seu ponto mais baixo. Visto em termos de energia, a energia potencial gravitacional do sistema de montanha-russa é convertida em energia cinética. Se o trabalho feito por atrito é insignificante, todo o ΔPEg é convertido para KE.
estratégia
a montanha-russa perde energia potencial à medida que desce. Negligenciamos o atrito, de modo que a força restante exercida pela pista é a força normal, que é perpendicular à direção do movimento e não trabalha. O trabalho de rede Na montanha-russa é então feito apenas pela gravidade. A perda de energia potencial gravitacional de se mover para baixo através de uma distância h é igual ao ganho de energia cinética. Isto pode ser escrito na forma de equação como-ΔPEg = ΔKE. Usando as equações de PEg e KE, podemos resolver para a velocidade final v, que é a quantidade desejada.
solução para a parte 1
Aqui a energia cinética inicial é zero, de modo que \Delta\text{KE}=\frac{1}{2}mv^2\\. A equação para a mudança na energia potencial afirma que ΔPEg = mgh. Uma vez que h é negativo neste caso, vamos reescrever este como ΔPEg = −mg|h| para mostrar o sinal de menos claramente. Assim, – ΔPEg = ΔKE torna-se mg|h|=\frac{1}{2}{mv}^2\\.
resolução para v, descobrimos que a massa cancela e que v = \sqrt{2g / h/}\.
Substituindo os valores conhecidos,
\begin{array}{lll}v&&\sqrt{2\left(9.80\text{ m/s}^2\right)\left(20.0\text{ m}\right)}\\\text{ }&&19.8\text{ m/s}\end{array}\\
Solução para a Parte 2
Novamente −ΔPEg = ΔKE. Neste caso existe energia cinética inicial, por isso
\ Delta\text{KE}=\frac{1}{2}mv^2 – \frac{1}{2}mv_0^2\\.
assim, mg/h / = \frac{1}{2}mv^2 – \frac{1}{2}mv_0^2\\.
rearranjar dá \frac{1}{2}mv^2=mg|h|+\frac{1}{2}mv+0^2\\.isto significa que a energia cinética final é a soma da energia cinética inicial e da energia potencial gravitacional. A massa volta a cancelar, e v=\sqrt{2g / h|+v_0^2}\\.
Esta equação é muito semelhante à cinemática equação v=\sqrt{v_0^2+2ad}\\, mas é mais geral—a cinemática equação é válida somente para a aceleração constante, enquanto que a nossa equação acima é válida para qualquer caminho, independentemente de se o objeto se move com uma aceleração constante. Agora, substituindo os valores conhecidos dá
\begin{array}{lll}v&&\sqrt{2\left(9.80\text{ m/s}^2\right)\left(20.0\text{ m}\right)+\left(5.00\text{ m/s}\right)^2}\\\text{ }&&20.4\text{ m / s}\end{array}\ \
discussão e implicações
primeiro, note que a massa cancela. Isto é bastante consistente com as observações feitas em objetos em queda que todos os objetos caem na mesma taxa se o atrito é insignificante. Em segundo lugar, apenas a velocidade da montanha-russa é considerada; não há informações sobre sua direção em nenhum ponto. Isto revela outra verdade geral. Quando o atrito é insignificante, a velocidade de um corpo em queda depende apenas da sua velocidade e altura iniciais, e não da sua massa ou do caminho percorrido. Por exemplo, a montanha-russa terá a mesma velocidade final se cair 20,0 m para baixo ou se tomar um caminho mais complicado como o da figura. Terceiro, e talvez inesperadamente, a velocidade final na parte 2 é maior do que na parte 1, mas por muito inferior a 5,00 m/s. Finalmente, note que a velocidade pode ser encontrado em qualquer altura ao longo do caminho, simplesmente utilizando o valor de h no ponto de interesse.
vimos que o trabalho feito por ou contra a força gravitacional depende apenas dos pontos inicial e final, e não do caminho entre, permitindo-nos definir o conceito simplificador da energia potencial gravitacional. Podemos fazer o mesmo por algumas outras forças, e veremos que isso conduz a uma definição formal da lei de conservação da energia.
Making Connections: Take-Home Investigation-Converting Potential to Kinetic Energy
pode-se estudar a conversão da energia potencial gravitacional em energia cinética neste experimento. Em uma superfície lisa e plana, use uma régua do tipo que tem um sulco correndo ao longo de seu comprimento e um livro para fazer uma inclinação (ver Figura 5). Colocar um mármore na posição de 10 cm sobre a régua e deixá-lo rolar para baixo a régua. Quando atingir a superfície do nível, medir o tempo que leva para rolar um metro. Agora coloque o mármore nas posições de 20 cm e 30 cm e novamente medir os tempos que leva para rolar 1 m na superfície do nível. Encontre a velocidade do mármore na superfície do nível para todas as três posições. Traçar velocidade ao quadrado contra a distância percorrida pelo mármore. Qual é a forma de cada trama? Se a forma é uma linha reta, o gráfico mostra que a energia cinética do mármore no fundo é proporcional à sua energia potencial no ponto de liberação.

Figura 5. Um mármore rola uma régua, e sua velocidade na superfície do nível é medida.
Resumo da secção
- Trabalho feito contra a gravidade na elevação de um objeto torna-se energia potencial do sistema objeto-Terra.
- A mudança na energia potencial gravitacional, ΔPEg, é ΔPEg = mgh, com h sendo o aumento na altura e g a aceleração devido à gravidade.a energia potencial gravitacional de um objeto próximo à superfície da terra deve-se à sua posição no sistema massa-Terra. Apenas as diferenças na energia potencial gravitacional, ΔPEg, têm significado físico.
- Como um objeto desce sem atrito, sua energia potencial gravitacional alterações em energia cinética correspondente ao aumento de velocidade, de modo que ΔKE = −ΔPEg
Questões Conceituais
- No Exemplo 2, podemos calcular a velocidade final de uma montanha-russa que desceu 20 m de altura e tinha uma velocidade inicial de 5 m/s downhill. Suponha que a montanha-russa tinha uma velocidade inicial de 5 m/s subindo em vez disso, e ela subiu subindo, parou, e então rolou de volta para um ponto final 20 m abaixo do início. Nesse caso, verificaríamos que tinha a mesma velocidade final. Explique em termos de conservação de energia.o trabalho que faz num livro quando o levanta numa prateleira depende do caminho percorrido? No tempo necessário? Na altura da prateleira? Na missa do livro?
Problemas & Exercícios
- Uma usina de energia hidrelétrica (ver Figura 6) converte a energia potencial gravitacional da água atrás de uma represa para energia elétrica. (a) qual é a energia potencial gravitacional em relação aos geradores de um lago de volume 50.0 km3 (massa = 5,00 × 1013 kg), dado que o lago tem uma altura média de 40,0 m acima dos geradores? B) Compare isto com a energia armazenada numa bomba de fusão de 9 megatoneladas.

Figura 6. Instalação hidroeléctrica (crédito: Denis Belevich, Wikimedia Commons)
- (a) o Quanto de energia potencial gravitacional (em relação ao solo sobre o qual ele é construído) é armazenado na Grande Pirâmide de Quéops, dado que a sua massa é cerca de 7 × 109 kg e o seu centro de massa é de 36.5 m acima do solo circundante? b) como é que esta energia se compara com a ingestão diária de alimentos de uma pessoa?suponha que um kookaburra 350-g (um grande pássaro kingfisher) pega uma cobra 75-g e levanta-a 2,5 m do chão para um ramo. (a) quanto trabalho fez o pássaro na cobra? (b) quanto trabalho fez para elevar seu próprio centro de massa para o ramo?
- no Exemplo 2, descobrimos que a velocidade de uma montanha-russa que tinha descido 20,0 m era apenas ligeiramente maior quando tinha uma velocidade inicial de 5,00 m/s do que quando começou do repouso. Isto implica que ΔPE >> KEi. Confirmar esta declaração tomando a relação ΔPE / KEi. (Note que a massa cancela.um carro de brinquedo de 100 g é movido por uma mola comprimida que o faz mover. O carro segue a pista curva na Figura 7. Mostrar que a velocidade final do carro de brinquedo é de 0,687 m/s se a sua velocidade inicial é de 2,00 m/s e encostas acima do declive sem fricção, ganhando 0,180 m em altitude.

Figura 7. Um carro de brinquedo move-se por uma pista inclinada. (crédito: Leszek Leszczynski, Flickr)
- em uma corrida de esqui downhill, surpreendentemente, pouca vantagem é ganha por começar a correr. (Isto porque a energia cinética inicial é pequena em comparação com o ganho em energia potencial gravitacional Em mesmo pequenas colinas.) Para demonstrar isso, encontrar a velocidade final e o tempo necessário para um esquiador que voa 70,0 m ao longo de uma inclinação de 30º desclassificando o atrito: (a) começando do descanso. B) começando com uma velocidade inicial de 2,50 m/S. c) a resposta surpreende-o? Discuta por que ainda é vantajoso começar a correr em eventos muito competitivos.
Glossário
energia potencial gravitacional: a energia que um objeto possui, devido à sua posição em um campo gravitacional
Selecionado Soluções para os Problemas & Exercícios
1. (a) 1,96 × 1016 J; (B) A razão entre a energia potencial gravitacional no lago e a energia armazenada na bomba é 0,52. Ou seja, a energia armazenada no lago é aproximadamente metade da de uma bomba de fusão de 9 megatoneladas.3. (a) 1, 8 J; (b) 8, 6 J
5. {v}_{f}=\sqrt{2gh+{v_0}^2}=\sqrt{2\left(9.80\text{ m/s}^2\right)\left(-0.180\text{ m}\right)+\left(2.00\text{ m/s}\right)^2}=0.687\text{ m/s}\\