After understanding the exponential function, our next target is the natural logarithm.

dada a forma como o log natural é descrito nos livros de matemática, há pouco “natural” sobre ele: é definido como o inverso de $e^x$, um expoente estranho o suficiente já.

mas há uma explicação nova e intuitiva: o log natural dá-lhe o tempo necessário para atingir um certo nível de crescimento.

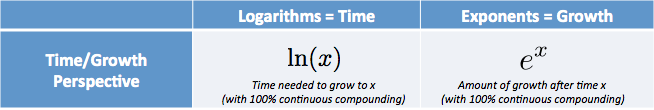
suponha que tem um investimento em gomas (quem não tem?) com uma taxa de juro de 100% ao ano, crescendo continuamente. Se você quiser um crescimento de 10x, assumindo uma composição contínua, você esperaria apenas $\ln (10)$ ou 2.302 anos. Não vês porque é que só leva alguns anos para ter crescimento de 10x? Não vejo porque o padrão não é 1, 2, 4, 8? Leia mais sobre E.

e e o Log natural são gêmeos:

• $e^x$ é a quantidade que temos depois de começar em 1.0 e crescer continuamente por $ X $ unidades de tempo
• $\ln (x)$ (logaritmo Natural) é o momento de chegar ao valor $x$, assumindo que crescemos continuamente de 1,0

não muito mal, certo? Enquanto os matemáticos se esforçam para lhe dar a longa e técnica explicação, vamos mergulhar na intuitiva.

e é sobre crescimento

o número e é sobre crescimento contínuo. Como vimos da última vez, $e^x$ nos permite fundir taxa e tempo: 3 anos a 100% de crescimento é o mesmo que 1 ano a 300% de crescimento, quando continuamente composto.

Podemos tomar qualquer combinação de taxa e tempo (50% para 4 anos) e converter a taxa para 100% por conveniência (dando-nos 100% para 2 anos). Convertendo para uma taxa de 100%, nós só temos de pensar sobre o componente de tempo de:

Intuitivamente, $e^x$ significa:

• Como o crescimento muito que recebo depois de x unidades de tempo (e de 100% de crescimento contínuo)
• Por exemplo: depois de 3 períodos de tempo eu ter $e^3$ = 20.08 vezes a quantidade de “coisas”.

$e^x$ é um fator de escala, mostrando-nos quanto crescimento teríamos após us $x$ unidades de tempo.

Log Natural é sobre o tempo

o log natural é o inverso de $e^x$, um termo de fantasia para o oposto. Por falar em Fantasia, o nome em latim é logarithmus naturali, dando a abreviatura ln.o que significa esta coisa inversa ou oposta?

• $e^x $ permite-nos ligar no tempo e crescer.
• $\ln( x) $ permite-nos ligar o crescimento e obter o tempo que levaria.

por exemplo:

• $e^3$ é 20.08. Depois de 3 unidades de tempo, acabamos com 20.Oito vezes mais do que começámos.
• $\ln (20.08)$ é cerca de 3. Se queremos um crescimento de 20.08, esperaríamos 3 unidades de tempo (novamente, assumindo uma taxa de crescimento 100% contínua).comigo? O log natural nos dá o tempo necessário para atingir o crescimento desejado.
  

  aritmética logarítmica não é Normal

  você já estudou registros antes, e eles eram animais estranhos. Como transformaram a multiplicação em adição? Divisão em subtracção? Vejamos.o que é $\ln (1)$? Intuitivamente, a questão é: quanto tempo eu espero para obter 1x minha quantidade atual?

  Zero. Postal. Nada. Você já está em 1x o seu valor atual! Não é preciso tempo para crescer de 1 para 1.

  • $\ln ( 1) = 0$

  Ok, que tal um valor fraccional? Quanto tempo para receber 1/2 da minha quantia actual? Assumindo que você está crescendo continuamente a 100%, sabemos que $\ln(2)$ é a quantidade de tempo para dobrar. Se nós o revertemos (isto é, tomar o tempo negativo) nós teríamos metade de nosso valor atual.

  • $\ln(.5) = – \ln (2)= -.693$

  faz sentido, certo? Se recuarmos .693 unidades (segundos negativos, digamos) teríamos metade da nossa quantidade actual. Em geral, você pode virar a fração e tomar o negativo: $\ln(1/3) = – \ln (3) = -1.09$. Isto significa que se recuarmos 1,09 unidades de tempo, teremos um terço do que temos agora.

  Ok, que tal o log natural de um número negativo? Quanto tempo demora a “cultivar” a colónia de bactérias de 1 a 3?é impossível! Não podes ter uma quantidade “negativa” de bactérias, pois não? No máximo (er… pelo menos) você pode ter zero, mas não há nenhuma maneira de ter uma quantidade negativa dos pequenos critters. As bactérias negativas não fazem sentido.

  • $\ln (\text{negative number}) = \text{undefined}$

  indefinido apenas significa “não há tempo que possa esperar” para obter uma quantia negativa. (Bem, se usarmos exponenciais imaginários, há uma solução. Mas hoje vamos ser realistas.)

  a multiplicação logarítmica é muito divertida

  quanto tempo demora a crescer 9x a sua quantidade actual? Claro, podemos usar a ln (9). Mas isso é muito fácil, vamos ser diferentes.

  Podemos considerar o crescimento de 9x como triplicado (levando $ \ ln (3)$ unidades de tempo) e depois triplicar novamente (tomando mais $\ln (3)$ unidades de tempo):

  • tempo para crescer 9x = $\ln(9)$ = tempo para triplicar e triplicar novamente = $\ln(3) + \ln(3)$

  interessante. Qualquer número de crescimento, como 20, pode ser considerado crescimento 2x seguido de crescimento 10x. Crescimento 4x seguido de crescimento 5x. Crescimento 3x seguido de 6.666 x crescimento. Vês o padrão?

  • $\ln(a * b) = \ln(a) + \ln(b)$

  o registo de A vezes b = log(a) + log (B). Esta relação faz sentido quando pensamos em termos de tempo para crescer.

  Se queremos crescer 30x, podemos esperar $\ln (30)$ de uma só vez, ou simplesmente esperar $\ln(3)$, para triplicar, em seguida, esperar $\ln(10)$, para Crescer 10x novamente. O efeito líquido é o mesmo, então o tempo líquido deve ser o mesmo também (e é).que tal divisão? $\ln (5/3)$ significa: Quanto tempo leva para crescer 5 vezes e, em seguida, tomar 1/3 disso?bem, crescer 5 vezes é $\ln (5)$. Crescer 1/3 é $ – \ln (3)$ unidades de tempo. Então

  • $\ln(5/3) = \ln(5) – \ln (3)$

  que diz: cresça 5 vezes e “volte no tempo” até que você tenha um terço dessa quantidade, então você fica com um crescimento de 5/3. Em geral temos

  • $\ln (a / b) = \ln (a) – \ln (b)$

  espero que a estranha matemática dos logaritmos esteja a começar a fazer sentido.: a multiplicação do crescimento torna-se adição do tempo, a divisão do crescimento torna-se subtração do tempo. Não memorizes as regras, entende-as.

  usando Logs naturais com qualquer taxa

  “claro”, você diz, ” Esta Coisa de log funciona para um crescimento de 100%, mas e quanto aos 5% que normalmente recebo?não há problema. O ” tempo “que recebemos de $\ln()$ é na verdade uma combinação de taxa e tempo, o” x ” da nossa equação de $e^x$. Assumimos 100% para simplificar, mas podemos usar outros números.suponha que queremos um crescimento de 30x: plug in $\ln (30)$ and get 3.4. O:

  • $e^x = \text{growth}$
  • $e^{3.4} = 30$

  e intuitivamente esta equação significa “100% de retorno durante 3,4 anos é 30x de crescimento”. Podemos considerar a equação a ser:

  

  

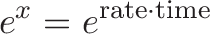
  podemos modificar “taxa” e “tempo”, enquanto a taxa de * tempo = 3.4. Por exemplo, suponha que queremos um crescimento de 30x — quanto tempo Esperamos assumindo 5% de retorno?

  • $\ln (30) = 3.4$
  • $\text{rate} * \text{time} = 3.4$
  • $.05 * \text{time} = 3.4$
  • $\text{time} = 3.4 / .05 = 68 \text{years}$

  intuitivamente, eu acho que ” $\ln (30) = 3,4$, então a 100% de crescimento levará 3,4 anos. Se duplicar a taxa de crescimento, reduzo para metade o tempo necessário.”

  • 100% para 3,4 anos = 1.0 * 3.4 = 3.4
  • 200% 1,7 anos = 2.0 * 1.7 = 3.4
  • 50% para 6,8 anos = 0.5 * 6.8 = 3.4
  • 5% para 68 anos = .05 * 68 = 3, 4

  Cool, eh? O log natural pode ser usado com qualquer taxa de juros ou tempo, desde que seu produto seja o mesmo. Podes mexer as variáveis o quanto quiseres.exemplo impressionante: a regra de 72

  a regra de 72 é um atalho mental de matemática para estimar o tempo necessário para dobrar o seu dinheiro. Vamos retirá-lo (yay!) e ainda melhor, vamos entendê-lo intuitivamente.quanto tempo demora a dobrar o seu dinheiro a 100% de juros, acrescido todos os anos?Oh. Temos usado log natural para taxas contínuas, mas agora estás a pedir juros anuais? Isto não vai estragar a nossa fórmula? Sim, vai, mas a taxas de juro razoáveis como 5%, 6% ou mesmo 15%, não há muita diferença entre juros anuais compostos e totalmente contínuos. Então a fórmula bruta funciona, mais ou menos, e vamos fingir que estamos a ter um interesse contínuo.

  Agora a questão é fácil: quanto tempo para dobrar a 100% de juros? ln (2) = .693. É preciso .693 unidades de tempo (anos, neste caso) para dobrar o seu dinheiro com composição contínua com uma taxa de 100%.Ok, e se o nosso interesse não for 100% e se for 5% ou 10%?

  simples. As long as rate * time = .693, vamos duplicar o nosso dinheiro:

  • Taxa * tempo = .693
  • tempo=.693 / rate

  So, if we only had 10% growth, it would take .693 / .10 ou 6,93 anos para o dobro.

  para simplificar as coisas, vamos multiplicar por 100 para que possamos falar sobre 10 em vez de .10:

  • tempo para dobrar = 69.3 / Taxa, onde a taxa é assumida como sendo em percentagem.

  Agora o tempo para dobrar a 5% de crescimento é 69, 3/5 ou 13, 86 anos. No entanto, 69.3 não é o número mais divisível. Vamos escolher um vizinho próximo, 72, que pode ser dividido por 2, 3, 4, 6, 8 e muitos mais números.

  • tempo para duplicar = 72/taxa

  que é a regra de 72! Calma.

  Se você quiser encontrar o tempo para triplicar, você usaria ln (3) ~ 109.8 e obter

  • tempo para triplicar = 110 / rate

  Que é outra regra útil de polegar. A regra de 72 é útil para taxas de juros, crescimento populacional, culturas de bactérias, e qualquer coisa que cresce exponencialmente.para onde?

  espero que o log natural faça mais sentido — ele diz-lhe o tempo necessário para qualquer quantidade de crescimento exponencial. Eu considero “natural” porque e é a taxa universal de crescimento, então ln poderia ser considerado a maneira” universal ” de descobrir quanto tempo as coisas levam para crescer.

  Quando você vê $\ln (x)$, basta pensar “a quantidade de tempo para crescer para x”. No próximo artigo vamos juntar e e ln, e o doce aroma da matemática vai encher o ar.

  Appendix: The Natural Log of E

  Quick quiz: What’s $\ln(e)$?

  • o robô matemático diz: porque eles são definidos como funções inversas, claramente $\ln(E) = 1$
  • o humano intuitivo: ln (e) é a quantidade de tempo que leva para obter “e” unidades de crescimento (cerca de 2.718). Mas e é a quantidade de crescimento após 1 unidade de tempo, então $\ln(e) = 1$.

  pense intuitivamente.

  Outros Posts Desta Série

  1. Uma interface Intuitiva Guia De Funções Exponenciais & e
  2. Desmistificando o Logaritmo Natural (ln)
  3. Um Guia Visual Simples, Composto e Contínua Taxas de Juros
  4. Definições Comuns de e (Colorida)
  5. a Compreensão Expoentes (Por que 0^0 = 1?)
  6. usando logaritmos no mundo Real
  7. Como pensar com expoentes e logaritmos
  8. compreendendo crescimento discreto vs. contínuo
  9. O que um expoente realmente significa?Q: Porque é que o e é especial? (2.718…, não 2, 3.7 ou outro número?)