a Lei de Boyle
Robert Boyle (1627 – 1691), um químico inglês, amplamente considerado como um dos fundadores da moderna ciência experimental da química. Ele descobriu que dobrar a pressão de uma amostra fechada de gás, mantendo sua temperatura constante, fez com que o volume do gás fosse reduzido para metade. A lei de Boyle afirma que o volume de uma determinada massa de gás varia inversamente com a pressão quando a temperatura é mantida constante. Uma relação inversa é descrita desta forma. À medida que uma variável aumenta em valor, a outra variável diminui.fisicamente, o que está a acontecer? As moléculas de gás estão se movendo e estão a uma certa distância uma da outra. Um aumento na pressão empurra as moléculas para mais perto, reduzindo o volume. Se a pressão é diminuída, os gases são livres para mover-se em um volume maior.

matematicamente, a lei de Boyle pode ser expressa pela equação:
\
O \(k\) é uma constante para uma dada amostra de gás e depende apenas da massa do gás e da temperatura. A tabela abaixo mostra dados de pressão e volume para uma quantidade definida de gás a uma temperatura constante. A terceira coluna representa o valor da constante \(\esquerda( k \direita)\) para estes dados e é sempre igual à pressão multiplicada pelo volume. À medida que uma das variáveis muda, as outras alterações de tal forma que o produto de \(P \vezes V\) permanece sempre o mesmo. Neste caso específico, essa constante é \(500\: \text{atm} \cdot \text{mL}\).
| Pressure \(\left( \text{atm} \right)\) | Volume \(\left( \text{mL} \right)\) | \(P \times V = k\) \(\left( \text{atm} \cdot \text{mL} \right)\) |
|---|---|---|
| 0.5 | 1000 | 500 |
| 0.625 | 800 | 500 |
| 1.0 | 500 | 500 |
| 2.0 | 250 | 500 |
| 5.0 | 100 | 500 |
| 8.0 | 62.5 | 500 |
| 10.0 | 50 | 500 |
Um gráfico com os dados na tabela ilustra a relação inversa natureza de Lei de Boyle (consulte a figura abaixo). O Volume é representado no eixo \(x\), com a pressão correspondente no eixo \(y\).
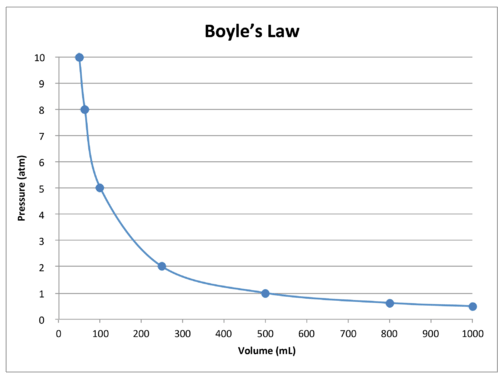
Boyle’s Law can be used to compare changing conditions for a gas. Nós usamos \(P_1\) e \(V_1\) para representar a pressão inicial e o volume inicial de um gás. Depois de uma alteração ter sido feita, \(P_2\) e \(V_2\) representam a pressão final e o volume. A relação matemática da Lei de Boyle torna-se:
\
esta equação pode ser usada para calcular qualquer uma das quatro quantidades se as outras três forem conhecidas.
exemplo \(\PageIndex{1}\)
uma amostra de gás oxigenado tem um volume de \(425 \: \text{mL}\) quando a pressão é igual a \(387 \: \text{kPa}\). O gás pode expandir-se para um contentor \(1, 75 \: \text{l}\). Calcular a nova pressão do gás.
solução
Passo 1: enumere as quantidades conhecidas e planeie o problema.
Conhecido
- \(P_1 = 387 \: \text{kPa}\)
- \(V_1 = 425 \: \text{mL}\)
- \(V_2 = 1.75 \: \text{L} = 1750 \: \text{mL}\)
Desconhecido
- \(P_2 = ? \ : \text{kPa}\)
Use a Lei de Boyle para resolver a pressão desconhecida \(\esquerda( P_2 \direita)\). É importante que os dois volumes (\(V_1\) e \(v_2\)) sejam expressos nas mesmas unidades, por isso \(V_2\) foi convertido para \(\text{mL}\).
Passo 2: resolver.
primeiro, reorganizar a equação algebricamente para resolver para \(P_2\).
\
Agora substituir as quantidades conhecidas na equação e resolver.
\
passo 3: pense no seu resultado.
o volume aumentou para um pouco mais de 4 vezes o seu valor original e assim a pressão é diminuída em cerca de um quarto. A pressão está em \(\text{kPa}\) e o valor tem três figuras significativas. Note que quaisquer unidades de pressão ou volume podem ser usadas desde que sejam consistentes ao longo de todo o problema.