Algebra to świetna zabawa – możesz rozwiązywać zagadki!
zagadka
czego brakuje?
| − | 2 | = | 4 |
ok, odpowiedź to 6, prawda? Ponieważ 6 − 2 = 4. Łatwizna.
cóż, w algebrze nie używamy pustych pól, używamy litery (Zwykle x lub y, ale każda litera jest dobra). Więc piszemy:
| x | − | 2 | = | 4 |
to naprawdę takie proste. Litera (w tym przypadku X) oznacza po prostu „jeszcze tego nie wiemy” i często nazywana jest nieznaną lub zmienną.
i kiedy go rozwiążemy piszemy:
| x | = | 6 |
Why Use a Letter?
| Because: | |
| it is easier to write „x” than drawing empty boxes (and easier to say „x” than „the empty box”). | |
| jeśli istnieje kilka pustych pól (kilka „niewiadomych”), możemy użyć innej litery dla każdego z nich. |
więc x jest po prostu lepszy niż posiadanie pustego pola. Nie próbujemy z nim rozmawiać!
i nie musi to być x, może to być y lub W… lub jakąkolwiek literę lub symbol, który nam się podoba.
jak rozwiązać
Algebra jest jak układanka, w której zaczynamy od czegoś w rodzaju „x − 2 = 4” i chcemy skończyć z czymś w rodzaju „x = 6”.
ale zamiast mówić „oczywiście x=6”, Użyj tego zgrabnego podejścia krok po kroku:
- dowiedz się, co usunąć, aby uzyskać „x = …”
- usuń go, robiąc odwrotnie (dodawanie jest przeciwieństwem odejmowania)
- zrób to po obu stronach
oto przykład:
usunąć
„-2”
![]()
aby go usunąć, wykonaj
odwrotnie, w
tym przypadku dodaj 2
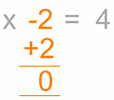
zrób to, aby
obie strony
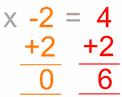
co jest …
![]()
![]()
dlaczego dodaliśmy 2 do obu stron?
aby „zachować równowagę”…
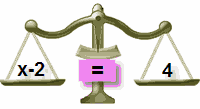
w równowadze
dodaj 2 do lewej strony

dodaj 2 do prawej strony również
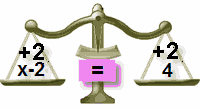
ponownie w równowadze
pamiętaj tylko o tym:
aby zachować równowagę, to, co robimy z jedną stroną „=”
, powinniśmy zrobić również z drugą stroną!
See this in action at the Algebra Balance Animation.
Another Puzzle
Solve this one:
| x | + | 5 | = | 12 |
What we want is an answer like „x = …”,
but the +5 is in the way of that!
możemy anulować +5 za pomocą -5 (ponieważ 5-5=0)
spróbuj sam
teraz poćwicz na tym prostym arkuszu algebry, a następnie sprawdź swoje odpowiedzi. Spróbuj użyć kroków, które pokazaliśmy tutaj, a nie tylko zgadywać!
wypróbuj poniższe pytania, a następnie przeczytaj wstęp do algebry-mnożenie