kilka ciekawych rzeczy o kątach i okręgach.
- kąt wpisany
- twierdzenia kąta wpisanego
- przykład: jaka jest wielkość kąta POQ? (O jest środkiem koła)
- przykład: jaka jest wielkość kąta CBX?
- kąt w półkolu (twierdzenie Thalesa)
- kolejny dobry powód, dla którego działa
- przykład: jaka jest wielkość kąta BAC?
- znalezienie środka okręgu
- Czworokąt cykliczny
- przykład: jaki jest rozmiar kąta WXY?
kąt wpisany
Po pierwsze, definicja:
kąt wpisany: kąt utworzony z punktów leżących na obwodzie okręgu.
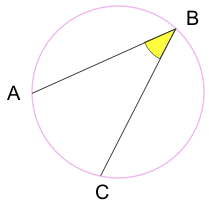
a i C to „punkty końcowe”
B to „punkt wierzchołkowy”
Zagraj z nim tutaj:
kiedy przesuniesz punkt „B”, co dzieje się z kątem?
twierdzenia kąta wpisanego
kąt wpisany a° jest połową kąta centralnego 2A°
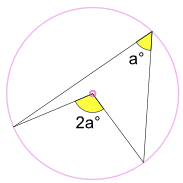
(zwany kątem w centrum twierdzenia)
i (utrzymując punkty końcowe stałe) …
… kąt a° jest zawsze taki sam,
bez względu na to, gdzie znajduje się na tym samym łuku między punktami końcowymi:
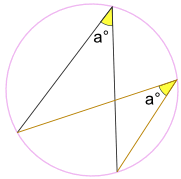
kąt A° jest taki sam.
(Angles Subtended by Same Arc Theorem)
przykład: jaka jest wielkość kąta POQ? (O jest środkiem koła)
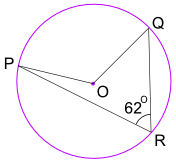
kąt POQ = 2 × Kąt PRQ = 2 × 62° = 124°
przykład: jaka jest wielkość kąta CBX?
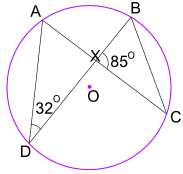
kąt ADB = 32° jest również równy kątowi ACB.
i kąt ACB również jest równy kątowi XCB.
więc w trójkącie BXC znamy kąt BXC = 85°, A kąt XCB = 32°
teraz używamy kątów trójkąta dodać do 180° :
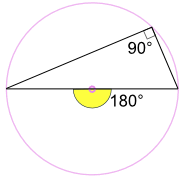
kąt w półkolu (twierdzenie Thalesa)
kąt wpisany w średnicy koła jest zawsze kątem prostym:

(punkty końcowe są albo końcem średnicy koła,
punkt wierzchołkowy może być wszędzie na obwodzie .)
|
Dlaczego? Ponieważ: wpisany kąt 90° jest połową środkowego kąta 180° (używając „kąta na środku” powyżej) |
 |
kolejny dobry powód, dla którego działa
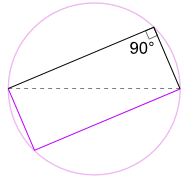
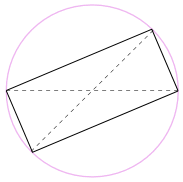
możemy również obróć kształt wokół 180°, aby utworzyć prostokąt!
jest to prostokąt, ponieważ wszystkie boki są równoległe, a obie przekątne są równe.
i tak jego kąty wewnętrzne są kątami prostymi (90°).
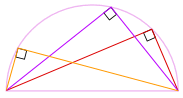
więc zaczynamy! Bez względu na to, gdzie jest ten kąt
na obwodzie, zawsze jest to 90°
przykład: jaka jest wielkość kąta BAC?
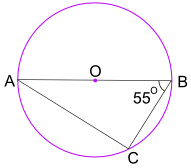
kąt w twierdzeniu półkola mówi nam, że kąt ACB = 90°
teraz użyj kątów trójkąta Dodaj do 180°, aby znaleźć kąt BAC:
znalezienie środka okręgu
możemy użyć tego pomysłu, aby znaleźć środek okręgu:
- narysuj kąt prosty z dowolnego miejsca na obwodzie okręgu, a następnie narysuj średnicę, w której obie nogi uderzają w okrąg
- zrób to jeszcze raz, ale dla innej średnicy
gdzie średnice przekraczają środek!
Czworokąt cykliczny
|
„Cykliczny” Czworokąt ma każdy wierzchołek na obwodzie koła: |
 |
|
Kąty odwrotne czworokąta do 180°:
|
 |
przykład: jaki jest rozmiar kąta WXY?
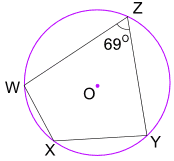
Opposite angles of a cyclic quadrilateral add to 180°
