Purplemath
w matematyce „tożsamość” jest równaniem, które jest zawsze prawdziwe. Mogą one być” trywialnie „prawdziwe, jak” x = x ” lub użytecznie prawdziwe, takie jak twierdzenie Pitagorasa „a2 + b2 = c2” dla trójkątów prostokątnych. Istnieje wiele tożsamości trygonometrycznych, ale poniżej są te, które są najbardziej prawdopodobne, aby zobaczyć i użyć.
Basic & Pythagorean, Angle-Sum & -Difference, Double-Angle, Half-Angle, Sum, Product
Content Continues Below
MathHelp.com
Need a custom math course?
K12 | College | Test Prep

podstawowe i pitagorejskie tożsamości
partner
zauważ, jak „co-(coś)” współczynnik trygonometryczny jest zawsze odwrotnością stosunku „non-co”. Możesz użyć tego faktu, aby pomóc ci zachować jasność, że cosecant idzie z sinusem, a secant z cosinusem.
następujące (szczególnie pierwsze z trzech poniżej) nazywa się tożsamościami „Pitagorejskimi”.
sin2(t) + cos2(T) = 1
tan2(T) + 1 = sec2(t)
1 + cot2(t) = csc2(t)
Reklama
zauważ, że trzy tożsamości przede wszystkim obejmują kwadrat i liczbę 1. Relację pitagorejską widać wyraźnie, jeśli weźmiemy pod uwagę okrąg jednostkowy, gdzie kąt to t, bok „przeciwny” to sin(t) = y, bok „sąsiedni” to cos(t) = x, a przeciwprostokątna to 1.
mamy dodatkowe tożsamości związane ze statusem funkcjonalnym współczynników trygonometrycznych:
sin(–t) = –sin(t)
cos(–t) = cos(T)
Tan(–t) = –Tan(t)
zauważ w szczególności, że sinus i styczna są funkcjami nieparzystymi, będąc symetrycznymi względem początku, podczas gdy cosinus jest funkcją parzystą, będąc symetrycznym względem Y-Y-Y-Y-Y-Y-Y-Y-Y-Y-Y-Y-Y-Y-Y-Y-Y-Y-Y-Y-Y-Y-Y-Y-Y-Y-Y-Y-Y-Y-Y-Y-Y-Y-Y-Y-Y-Y-Y-Y-Y-Y-Y-Y-Y-Y-Y-Y-Y-Y-Y-Y-Y-Y-Y-Y-Y-Y-Y oś. Fakt, że możesz wziąć znak „minus” argumentu na zewnątrz (dla sinusa i tangensa) lub całkowicie go wyeliminować (dla cosinusa), może być pomocny podczas pracy ze skomplikowanymi wyrażeniami.
kąt-Suma i-różnica tożsamości
sin(α + β) = sin(α) cos(β) + cos(α) sin(β)
sin(α – β) = sin(α) cos(β) – cos(α) sin(β)
cos(α + β) = cos(α) cos(β) – sin(α) sin(β)
cos(α – β) = cos(α) cos(β) + Sin(α) Sin(β)
nawiasem mówiąc, w powyższych tożsamościach kąty są oznaczone greckimi literami. Litera typu A, „α”, nazywa się „alfa”, która jest wymawiana”AL-fuh”. Litera typu B, „β”, nazywa się „beta”, która jest wymawiana”BAY-tuh”.
zawartość kontynuowana jest poniżej
tożsamości dwu-kątowe
Sin(2x) = 2 sin(x) cos(x)
cos(2x) = cos2(x) – sin2(x) = 1 – 2 sin2(x) = 2 cos2(x) – 1
tożsamości pół-kątowe
powyższe tożsamości można ponownie określić, kwadratując każdy bok i podwajając wszystkie miary kąta. Wyniki są następujące:
Affiliate

Sum Identities
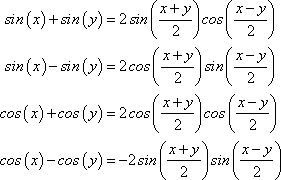
Product Identities
afiliacja
będziesz używać wszystkich tych tożsamości, lub prawie tak, do udowodnienia innych tożsamości Tryg i rozwiązywania równań Tryg. Jeśli jednak zamierzasz studiować rachunek różniczkowy, zwróć szczególną uwagę na przekształcone tożsamości półkąta sinusa i cosinusa, ponieważ będziesz ich często używał w rachunku całkowym.
URL: https://www.purplemath.com/modules/idents.htm