Królewiec to miasto nad rzeką Preger, które w XVIII wieku było miastem niemieckim, ale obecnie rosyjskim. W obrębie miasta znajdują się dwie wyspy, które są połączone z brzegami siedmioma mostami (jak pokazano poniżej).

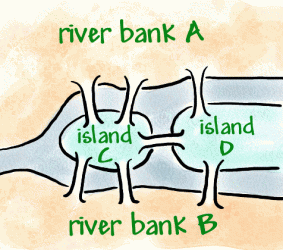
tradycją stało się chodzenie po mieście w sposób, który tylko raz przekroczył każdy most, ale okazał się trudnym problemem. Leonhard Euler, szwajcarski matematyk w służbie rosyjskiej cesarzowej Katarzyny Wielkiej, usłyszał o problemie.W 1736 roku Euler udowodnił, że spacer nie jest możliwy. Rozwinął to wymyślając rodzaj diagramu zwanego siecią, który składa się z wierzchołków (punktów, w których spotykają się linie) i łuków(linii).

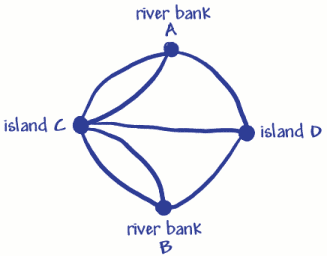
użył czterech punktów (wierzchołków) dla dwóch brzegów rzeki i dwóch krańców. Zostały one oznaczone A, B I C, D. siedem linii (łuków) to siedem mostów. Możesz zobaczyć, że 3 mosty (łuki)łączą się z brzegiem rzeki A, a 3 łączą się z brzegiem rzeki B. 5 mostów (łuki)łączy się z wyspą C, a 3 łączą się z wyspą D. Oznacza to, że wszystkiewersje mają nieparzystą liczbę łuków, więc nazywane są dziwnymi. (Parzysty wierzchołek musiałby mieć parzystą liczbę łuków).
pamiętaj, że problemem było poruszanie się po mieście przechodząc przez każdy most tylko raz. W sieci Eulera oznaczało to prześledzenie każdego z wierzchołków tylko raz, odwiedzając wszystkie wierzchołki. Euler udowodnił, że nie da się tego zrobić, ponieważ odkrył, że aby mieć dziwny wierzchołek, należy rozpocząć lub zakończyć podróż w tym wierzchołku. (Pomyśl o tym).Ponieważ może być tylko jeden początek i jeden koniec, mogą być tylko dwa nieparzyste wierzchołki, jeśli masz zamiar być w stanie prześledzić nad każdym z nich tylko raz. Ponieważ problem z mostem ma 4 nieparzyste wierzchołki, nie jest to możliwe! Co się stanie, jeśli w ogóle nie ma dziwnych wierzchołków? Czy można namierzyć tę sieć?

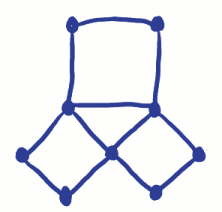
wynalezienie sieci zapoczątkowało zupełnie nowy typ geometrii, zwany „topologią”. Topologia jest obecnie wykorzystywana na wiele sposobów, w tym do planowania i mapowania sieci kolejowych. (Ahhh! Pociągi musiały wjeżdżać….)