ten dział obejmuje:

• Wprowadzenie do funkcji w kawałkach
• Ewaluacja funkcji w kawałkach
• wykresy funkcji w kawałkach
• Jak stwierdzić, czy funkcja w kawałkach jest ciągła czy nie
• uzyskiwanie równań z Wykresów funkcji w kawałkach
• wartość bezwzględna jako funkcja w kawałkach
• transformacje funkcji w kawałkach
• problemy ze słowem funkcji w kawałkach
• więcej praktyki

funkcje piecewise (lub funkcje piece-wise) są po prostu takie, jakie są nazwane: fragmenty różnych funkcji (pod-funkcji) wszystko na jednym wykresie. Najłatwiej o nich pomyśleć, jeśli narysowałeś więcej niż jedną funkcję na wykresie i po prostu wymazałeś części funkcji, w których nie powinny być (wzdłuż \(x\)’S); są one zdefiniowane inaczej dla różnych przedziałów \(x\). \(y\) jest różnie definiowane dla różnych wartości \(x\); używamy \(x\), aby sprawdzić, w jakim przedziale jest, abyśmy mogli dowiedzieć się, co to jest \(y\).

zauważ, że w sekcji odwrotności funkcji znajduje się przykład odwrotności funkcji.

Here’s an example and graph:

Piecewise Function

Graph

\(\displaystyle f\left( x \right)=\left\{ \begin{align}2x+8\,\,\,\,\,&\text{ if }x\le -2\\{{x}^{2}}\,\,\,\,\,\,\,\text{ }\,&\text{ if }x>-2\end{align} \right.\) (istnieją inne sposoby wyświetlania tego, takie jak użycie „for” zamiast „if” oraz użycie przecinków lub średników zamiast „if”.) domena: \(\mathbb{R},\,\,\, \ text{lub}\,\, \ left ({- \infty ,\infty } \right)\) zakres: \(\mathbb{R},\,\,\,\text{or}\,\, \left ({- \infty, \infty}\right)\)

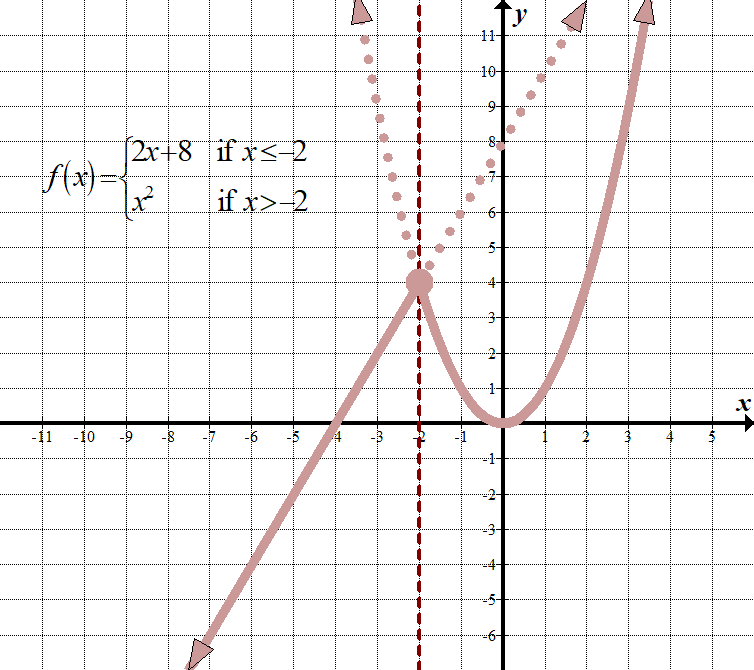oznacza to, że dla każdego\ (X\) mniejszego lub równego -2, musimy narysować linię\ (2x+8\), tak jakby była to jedyna funkcja na wykresie. Dla każdej wartości\ (x\) większej niż -2, musimy narysować wykres \({{x}^{2}}\), tak jakby była to jedyna funkcja na wykresie. Następnie musimy „pozbyć się” części, których nie potrzebujemy. Pamiętaj, że nadal Używamy origin jako punktu odniesienia dla obu Wykresów!

zobacz, jak pionowa linia \(x=-2\) działa jako linia „graniczna” między dwoma grafami?

zauważ, że punkt \((-2,4)\) ma zamknięty okrąg. Technicznie rzecz biorąc, powinna ona należeć tylko do funkcji \(2x+8\), ponieważ funkcja ta ma znak mniejszy lub równy, ale ponieważ punkt znajduje się również na wykresie \({{x}^{2}}\), możemy po prostu użyć zamkniętego okręgu tak, jakby pojawił się na obu funkcjach. Widzisz, nie tak źle, prawda?

Ewaluacja funkcji fragmentarycznych

czasami otrzymasz funkcje fragmentaryczne i poprosisz o ich ocenę; innymi słowy, znajdź wartości \(y\), gdy otrzymasz wartość \(x\). Zróbmy to dla \(x = -6\) i \(x = 4\) (bez użycia grafu). Oto ponownie funkcja:

\(\displaystyle f\left (x \right)=\left\ {\begin{align}2x+8\,\,\,\,\,& \ text{ if} x\le -2\ \ {{x}^{2}}\,\,\,\,\,\,\,\tekst { }\, &\text{ if }x> -2 \end{align} \ right.

najpierw chcemy przyjrzeć się Warunkom po prawej stronie, aby zobaczyć, gdzie znajduje się nasze \(x\). Gdy \(x=-6\), wiemy, że jest mniejsze niż -2, więc podłączamy nasze \(x\) Tylko do \(2x+8\). \(f(x)\) lub \(y\) jest \((2)(-6)+8=-4\). Nie dbamy nawet o \(\boldsymbol {{x}^{2}}\)! To takie proste. Możesz również zobaczyć, że zrobiliśmy to poprawnie, korzystając z powyższego wykresu.

teraz spróbuj \(x=4\). Najpierw patrzymy na prawo i widzimy, że nasze \(x\) jest większe niż -2, więc podłączamy go do \({{x}^{2}}\). (Możemy po prostu zignorować \(2x + 8\) tym razem.) \(f (x)\) lub \(y\) jest \({{4}^{2}}=16\).

Wykresowanie funkcji w kawałkach

prawdopodobnie zostaniesz poproszony o wykresowanie funkcji w kawałkach. Czasami wykresy będą zawierać funkcje, które nie są ciągłe lub nieciągłe, co oznacza, że musisz podnieść ołówek w środku wykresu, gdy go rysujesz(jak skok!). Funkcje ciągłe oznaczają, że nigdy nie musisz podnosić ołówka, jeśli rysujesz je od lewej do prawej.

i pamiętaj, że wykresy są prawdziwymi funkcjami tylko wtedy, gdy przechodzą Test linii pionowej.

narysujmy te funkcje i ustalmy, czy są ciągłe, czy nie. Zauważ, jak rysujemy każdą funkcję tak, jakby była jedyną, a następnie „kasujemy” części, które nie są potrzebne. Otrzymamy również dziedzinę i zakres, tak jak to zrobiliśmy w sekcji funkcji algebraicznych.

Piecewise Function	Graph
\(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}-2x+8\,\,\,\,\,\,\text{if }x\le 4\\\frac{1}{2}x-2\,\,\,\,\,\,\,\,\,\text{if }x>4\end{array} \right.\) Continuous Domain: \(\mathbb{R},\,\,\,\text{or}\,\,\left( {-\infty ,\infty } \right)\) Range: \(\left( {0,\infty } \right)\)
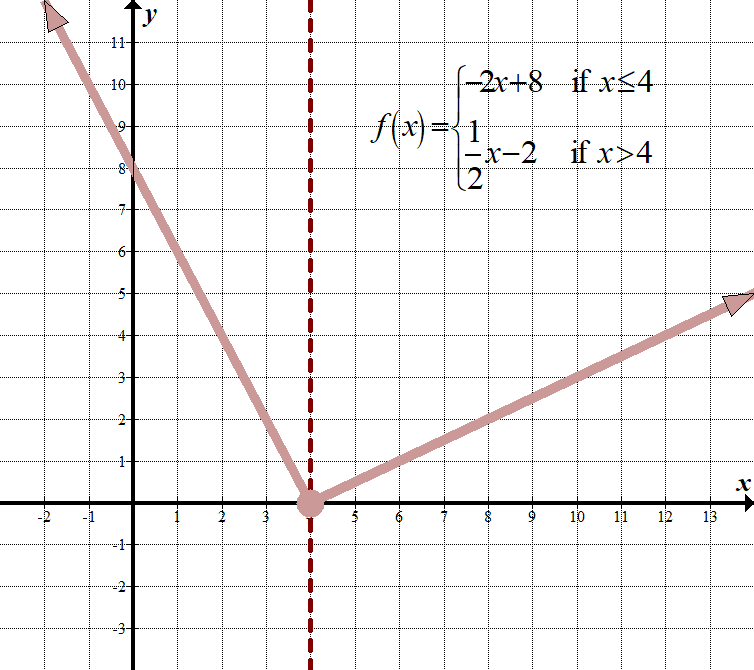\(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}x+4\,\,\,\,\,\,\,\,\,\text{if }x<1\\2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{if 1}\le x<4\\x-5\,\,\,\,\,\,\,\,\,\text{if }x\ge 4\end{array} \right.\) Non-Continuous Domain: \(\mathbb{R},\,\,\,\text{or}\,\,\left( {-\infty ,\infty } \right)\) Range: \(\mathbb{R},\,\,\,\text{or}\,\,\left( {-\infty ,\infty } \right)\)

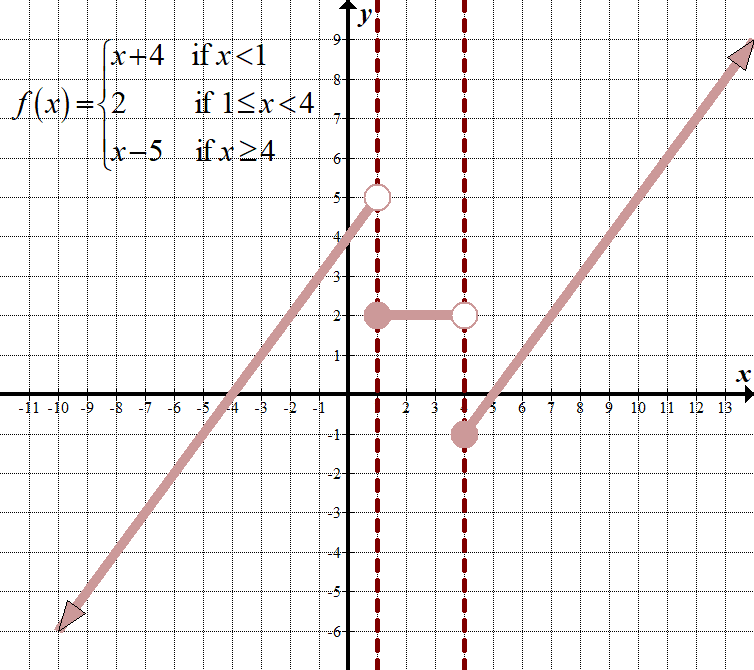We can actually put piecewise functions in the graphing calculator:

Piecewise Function Screens

Steps and Notes

Enter the piecewise function on three lines: oto wykres:

aby umieścić funkcję piecewise \(\displaystyle f\left( x \right)=\left\{ \begin{array}{L}x+4\,\,\,\,\,\,\,\,\,\text{if} x<1\\2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{if 1}\le x<4\ \ -5 + x\,\,\,\,\,\text{if} x\ge 4 \ end{array} \ right.\ ) w kalkulatorze można wprowadzić funkcję na trzy linie dzieląc funkcję w każdym przedziale przez „nierówność testową”tego przedziału (i obserwuj nawiasy!). dzielimy przez przedziały lub nierówności, ponieważ Kalkulator zwróci 1, jeśli nierówność (taka jak \(x<1\)) Jest Prawdziwa; na przykład \((x+4)\) po prostu skończy się \((x+4)/(1)\), Gdy \(x< 1\). Gdy \(x\ge 1\) dzielimy przez 0, więc nic nie zostanie narysowane. Oto, co możemy umieścić w kalkulatorze: \(\displaystyle \begin{array}{l}{{y}_{1}}=\left( {x+4} \right)/\left( {x<1} \right)\\{{y}_{2}}=\left( 2 \right)/\left( {x\ge 1\text{ I }X<4} \right)\\{{y}_{3}}=\Left( {-5+x} \right)/\left( {x\GE 4} \right)\end{array}\) (zauważ, że możesz również wprowadzić to w jednej linii, mnożąc warunki zamiast dzielenia i używając znaków plus między każdą z trzech funkcji/interwałów: \(\displaystyle {{Y}_{1}}=\left( {x+4} \right)\left( {x<1} \right)+\left( 2 \right)\left( {x\ge 1\text{ and }x<4} \right)+\left( {-5+x} \right)\left( {x\GE 4} \right)\).) oto naciśnięcia klawiszy za pomocą trzech linii. Zauważ, że używasz 2.MATH (TEST), aby dostać się do ekranu, który ma \(\le\), \(\ge\) i tak dalej. Na przykład, 2. matematyka 6 dostaje \(\le \). Użyj 2. MATH (TEST), prawo do logiki, a następnie 1, dla „I” W \({{y}_{2}}\).

spójrz na punkty graniczne i sprawdź, czy punkt \(y\) jest taki sam w każdym z nich. (Gdyby\(y\)’s były inne, byłby „skok” na wykresie!)

spróbujmy tego dla funkcji, których użyliśmy powyżej:

Piecewise Function	Check Boundary Points
\(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}-2x+8\,\,\,\,\,\,\,\text{if }x\le 4\\\frac{1}{2}x-2\,\,\,\,\,\,\,\,\,\,\text{if }x>4\end{array} \right.\)	Let’s check \(x=4\) in both parts of the function, since 4 is the „boundary point”: \(\begin{array}{l}-2(4)+8=0\\\,\,\,\frac{1}{2}(4)-2=0\end{array}\) ponieważ \(0=0\), ta funkcja jest ciągła.
\(\displaystyle f\left (x \right)=\left\ {\begin{array}{l}x+4\,\,\,\,\,\,\,\,\,\,\,\,\,\text{if} x<1\\2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{if 1}\le x<4\ \ -5 + x\,\,\,\,\,\,\,\,\,\text{if} x\ge 4 \ end{array} \ right.\)	sprawdźmy dwie pierwsze części funkcji. Uwaga w drugiej części, \(y\) jest zawsze 2: \(\begin{array}{l}1+4=5\\\,\,\,\,\,\,\,\,\,2=2\end{array}\) ponieważ \(5\ne 2\), możemy zatrzymać się tutaj i zauważyć, że ta funkcja jest nieciągła. Jeśli \ (y\) ’ S były równe, musielibyśmy przejść jeden, aby sprawdzić następny punkt graniczny w \(x=4\).

otrzymywanie równań z Wykresów funkcji fragmentarycznych

możesz zostać poproszony o napisanie funkcji fragmentarycznej, podanej na wykresie. Teraz, gdy wiemy, o co chodzi w funkcjach fragmentarycznych, nie jest tak źle!

aby przejrzeć, jak uzyskać równania z wykresów liniowych, zobacz uzyskiwanie równań linii, a z kwadratów, zobacz Znajdowanie równania kwadratowego z punktów lub wykresu.

oto wykresy, z wyjaśnieniami, jak wyprowadzić ich równania fragmentaryczne:

Piecewise Function Graph	Procedure to get Function
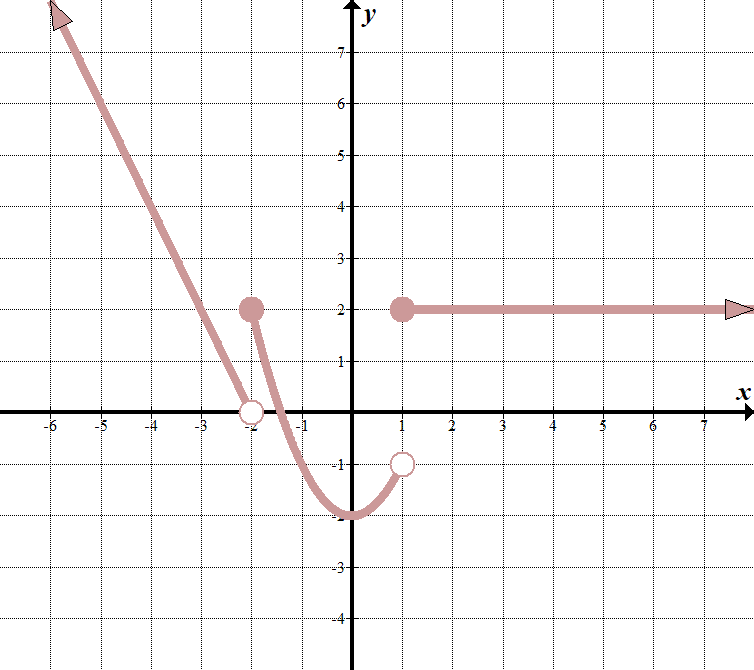	We see that our „boundary lines” are at \(x=-2\) and \(x=1\). We know that our function will look something like this (notice open and closed endpoints): \(\displaystyle f\left (x \right)=\left\ {\begin{array} {l} \ text{ }……\,\,\,\,\,\,\,\,\text{if} x< -2\\\text{ }……\,\,\,\,\,\,\,\,\text{if} – \text{2} \ le x< 1\\ \ text{ }……\,\,\,\,\,\,\,\,\text{if} x\ge 1 \ end{array} \ right.\) możemy wybrać dwa punkty \((-2,0)\) i \((-3,2)\) na lewej linii, aby uzyskać równanie \(y= – 2x-4\). środkową funkcją jest \(y = {{x}^{2}}-2\), a funkcja po prawej stronie to tylko pozioma linia \(y=2\). Tak więc funkcja fragmentaryczna jest: \(\displaystyle f\left (x \right)=\left\ {\begin{array}{l} – 2x-4\,\,\,\,\,\,\,\text{if} x< -2\ \ \ text { } {{x}^{2}}-2\,\,\,\,\,\,\,\,\,\,\text{if} – \text{2} \ le x< 1\\ \ text{ 2}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{if} x\ge 1 \ end{array} \ right.
	widzimy, że nasza „linia graniczna” znajduje się w \(x=5\). Ponieważ linie spotykają się w \((5,4)\), nie ma znaczenia, gdzie umieścimy znak \(\le \) lub \(\ge\); po prostu nie możemy umieścić tego w obu miejscach, inaczej nie byłoby to funkcją. Mamy do tej pory: \(\displaystyle f\left (x \right)=\left\ {\begin{array} {l} \ text{ }……\,\,\,\,\,\,\,\,\,\text{if} x< 5\\\text{ }……\,\,\,\,\,\,\,\,\,\text{if} x\ge 5 \ end{array} \ right.\) ponownie, musimy spojrzeć na każdą linię osobno, aby określić ich równania. Możemy albo wziąć 2 punkty z każdej linii, aby je otrzymać, albo wyprowadzać ze stoków i \(y\)–przechwytuje; funkcja piecewise jest: \(\displaystyle f\left (x \right)=\left\ {\begin{array} {l} \ frac{6}{5} x-2\,\,\,\,\,\,\,\text{if }x<5\\\frac{2}{5} x+2\,\,\,\,\,\,\,\text{if} x\ge 5 \ end{array} \ right.\)

wartość bezwzględna jako funkcja fragmentaryczna

możemy zapisać funkcje wartości bezwzględnej jako funkcje fragmentaryczne – to naprawdę fajne! Zanim przejdziesz do tego tematu, zapoznaj się z rozwiązywaniem równań i nierówności wartości bezwzględnej.

powiedzmy, że mamy funkcję \(f\left (x \right)=\left| x \right/\). Z tego, co dowiedzieliśmy się wcześniej, wiemy, że gdy \(x\) jest dodatnia, ponieważ bierzemy wartość bezwzględną, to nadal będzie ona po prostu \(x\). Ale kiedy \(x\) jest ujemne, kiedy bierzemy wartość bezwzględną, musimy wziąć odwrotną (zanegować ją), ponieważ wartość bezwzględna musi być dodatnia. Ma to sens? Na przykład, jeśli mamy \(/5/\), bierzemy to, co jest wewnątrz znaku absolutnego, ponieważ jest dodatnie. Ale dla \(/-5/\), musimy wziąć odwrotność (ujemną) tego, co jest wewnątrz wartości bezwzględnej, aby to zrobić \(\displaystyle 5\,\,\,(-\,-5=5)\).

oznacza to, że możemy zapisać tę funkcję wartości bezwzględnej jako funkcję fragmentaryczną. Zauważ, że możemy uzyskać „punkt zwrotny” lub „punkt graniczny”, ustawiając to, co jest wewnątrz wartości bezwzględnej na 0. Następnie albo użyjemy funkcji oryginalnej, albo zanegujemy funkcję, w zależności od znaku funkcji (bez wartości bezwzględnej) w tym przedziale.

na przykład możemy napisać \(\displaystyle \left / x \right / \ text{ }=\left\ {\begin{array}{l}x\,\,\,\,\,\,\,\,\,\text{if} x\ge 0\\ – x\,\,\,\,\,\text{if} x< 0 \ end{array} \ right.\). Zauważ również, że jeśli funkcja jest ciągła (nie ma” Skoku”) w punkcie granicznym, nie ma znaczenia, gdzie umieścimy znaki” mniejsze lub równe „(lub” większe lub równe”), o ile ich nie powtórzymy! Nie możemy ich powtórzyć, ponieważ teoretycznie nie możemy mieć dwóch wartości \(y\) dla tego samego \(x\), inaczej nie mielibyśmy funkcji.

Here are more examples, with explanations. (You might want to review Quadratic Inequalities for the second example below):

Absolute Value Function	Method to get Piecewise Function
\(g\left( x \right)=\left| {2x+3} \right|\)	Let’s first find the „boundary line”. Robimy to ustawiając to, co jest wewnątrz wartości bezwzględnej na 0, a następnie rozwiązując dla \(\boldsymbol{x}\). Gdy \(2x+3\ge 0\), otrzymujemy \(\displaystyle x\GE – \frac{3}{2}\) (w rzeczywistości możemy zachować \(\ge\), gdy rozwiążemy). Kiedy \(2x+3\) jest dodatnie, bierzemy to „tak jak jest”, ale jeśli jest ujemne, musimy zanegować całość. dlatego funkcja fragmentaryczna jest: \(\displaystyle \left / {2x+3} \right / = \left\ {\begin{array} {l}2x+3\,\,\,\,\,\,\,\,\,\text{if }x\GE -\frac{3}{2} \ text { } \\ – 2x-3\,\,\,\,\,\text{if }x<-\frac{3}{2}\end{array} \right. spróbuj-działa!
\(f\left( x \right)=\left|{{{x}^{2}}-4} \right/\)	znajdźmy najpierw „linię graniczną(y)”; ustawiamy wartość bezwzględną na 0. Kiedy \({{x}^{2}}-4\ge 0\), otrzymujemy \(x\ le -2\) lub\(x \ GE 2\) (Spróbuj kilka liczb!). Kiedy \({{x}^{2}}-4\) jest dodatnia, bierzemy ją „tak jak jest”, ale jeśli jest ujemna, musimy ją zanegować. funkcja piecewise to: \(\displaystyle \left / {{x}^{2}}-4} \ right / = \left\ {\begin{array} {l} {{x}^{2}}-4\,\,\,\,\,\text{if} x \ le -2\\4 – {{x}^{2}}\,\,\,\,\,\tekst{if }-2<x<2\ \ {{x}^{2}}-4\,\,\,\,\,\text{if} x\ge 2 \ text { } \ end{array} \ right.\ ) lub \(\displaystyle \ left / {{x}^{2}} -4} \right|= \ left\ {\begin{array} {l} {{x}^{2}}-4\,\,\,\,\,\,\text{if }x\le -2\text {}\,\, \ text {or}\,\, \ text {} x \ ge 2\\4 – {{x}^{2}}\,\,\,\,\,\,\,\tekst{if }-2<x<2\end{array} \right.\) ponownie (ponieważ funkcja jest ciągła), tak naprawdę nie ma znaczenia, gdzie mamy \(\le \) i \(\ge \) (W przeciwieństwie do \(<\) I \(>\)), o ile ich nie powtórzymy.
\(f\left( x \right)=2x+\left|{x+2} \right/\)	ten jest trochę trudniejszy, ponieważ mamy \(x\) Wewnątrz I Na Zewnątrz wartości bezwzględnej. Dla „linii granicznej” używamy tylko tego, co znajduje się wewnątrz wartości bezwzględnej. Gdy \(x+2\ge 0\), otrzymujemy \(x\GE -2\). Ale dla funkcji fragmentarycznej, musimy użyć całej funkcji, łącznie z częścią, która jest poza wartością bezwzględną. Funkcja fragmentaryczna jest więc: \(\displaystyle 2x+ \ left / {x+2} \right / = \left\ {\begin{array}{l}2x + x+2\,\,\,\,\,\text{if} x\ge -2\\2x-x-2\,\,\,\,\,\text{if} x< -2 \end{array} \ right. uprośćmy: \(\displaystyle 2x+ \ left / {x + 2} \right / = \left\ {\begin{array}{l}3x+2\,\,\,\,\,\,\,\text{if} x\ge -2\\x-2\,\,\,\,\,\,\,\,\,\,\text{if} x< -2 \end{array} \ right.\) spróbuj jakieś wartości mniejsze niż i Świetne wtedy -2; powinny działać!
\(g\left( x \right)=\left| {{{x}^{2}}-4x-5} \right|\)	ten najlepiej rozwiązać za pomocą wykresu znakowego, ponieważ mamy kwadrat i musimy wiedzieć, gdzie jest funkcja pozytywne i negatywne. Po pierwsze, współczynnik kwadratowy wewnątrz funkcji wartości bezwzględnej to \(\left ({x-5} \right) \ left ({x + 1} \right)\). Następnie użyj wykresu znakowego, aby zobaczyć, gdzie czynniki są dodatnie i ujemne, i pamiętaj, że gdzie czynniki są dodatnie, używamy funkcji „tak jak jest”, a gdzie czynniki są ujemne, negujemy funkcję: \(\displaystyle \ left / {{x}^{2}} – 4x-5} \ right/= \ left\ {\begin{array} {l} {{x}^{2}} – 4x-5\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{if} x\le -1\,\,\,\,\tekst{lub}\,\,\,\, x \ ge 5 \ \ – \ left ({{x}^{2}}-4x-5} \right)\,\,\,\,\tekst{if }-1<x<5\text{ }\end{array} \right.\)
\(\displaystyle g\left( x \right)=\frac{{\left| {x+2} \right|}}{{x+2}}\)	jest to funkcja racjonalna, ponieważ w mianowniku jest zmienna. Gdy \(x+2\ge 0\), otrzymujemy \(\displaystyle x\ge -2\). Kiedy \(x+2\) jest dodatnie, bierzemy to „tak jak jest”, ale jeśli jest ujemne, musimy zanegować to, co jest w wartości bezwzględnej: \(\displaystyle \frac{{\left / {x + 2} \right/}} {{x + 2}}=\left\ {\begin{array} {l}\frac {{x+2}} {{x+2}}\,\,\,\,\,\,\,\,\,\text{if} x\ge -2\ \ \ frac {{- x-2}}{{x+2}}\,\,\,\,\,\,\text{if} x< -2 \end{array} \ right.\). Ale musimy być ostrożni, ponieważ \(x\ne 2\) (ograniczenie domeny: mianownik będzie równy 0). dlatego funkcja fragmentaryczna jest: \(\displaystyle \frac{{\left / {x + 2} \right/}} {{x + 2}}= \ left\ {\begin{array} {l}1\,\,\,\,\,\,\,\,\,\,\text{if} x>-2\\-1\,\,\,\,\,\,\text{if} x< -2 \end{array} \ right.\).

Możesz również zostać poproszony o wzięcie wykresu wartości bezwzględnej i zapisanie go jako funkcji fragmentarycznej:

Absolute Value Graph	Method to get Piecewise Function
	We see that our „boundary line” is at \(x=0\), so what’s inside the absolute value sign must be \(x\) or a factor of \(x\). (Dzieje się tak, ponieważ aby uzyskać linię graniczną z funkcją wartości bezwzględnej, ustawiamy to, co jest wewnątrz wartości bezwzględnej na 0 i rozwiązujemy dla \(x\)). Gdy \(x> 0\), widzimy, że równanie linii to \(y = 2x-2\). Gdy \(x< 0\), równanie to \(y=2x-2\). Możemy to zapisać jako funkcję fragmentaryczną: \(\displaystyle f\left (x \right)=\left\ {\begin{array}{l}2x-2\,\,\,\,\,\,\,\text{if} x>0\\-2x-2\,\,\,\text{if }x\le 0\end{array} \right.\) możemy również zapisać to jako przekształconą funkcję wartości bezwzględnej: \(y=2\left| x \right|-2\) lub \(y=\left| {2x} \right|-2\) (ponieważ 2 jest dodatnie, może być wewnątrz lub na zewnątrz \(\left| {\,\,} \right|\)). (Ma to sens, ponieważ gdy to, co jest wewnątrz \(\left / { \ ,\,} \right/\) to \(>0\), używamy zwykłej funkcji \(y=2x-2\), a gdy to, co jest wewnątrz to \(< 0\), negujemy część wartości bezwzględnej, aby ją \(y=-\left( {2x} \ right) -2\)).
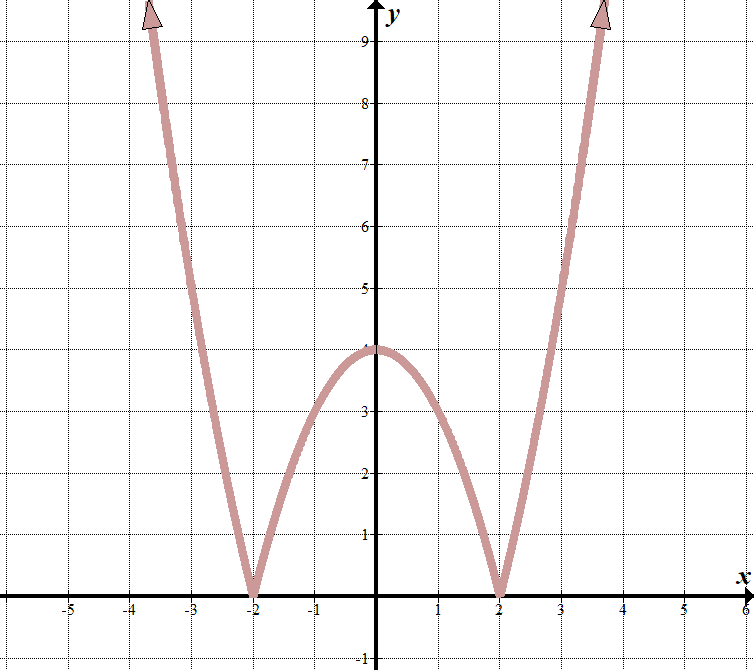	widzimy, że nasze „linie graniczne” są w \(x=2\) i \(x=-2\), więc to, co znajduje się wewnątrz znaku wartości bezwzględnej, musi mieć czynniki of \(X-2\) and \(X+2\). Gdy \(x<-2\) lub \(x>2\), widzimy, że wykres wygląda jak normalna część wykresu \(y={{x}^{2}}-4\). (Domyśliłem się tego, znając czynniki i dobrze zgadując!) Gdy \(-2<x<2\), równanie jest odwrócone lub zanegowane (odwrócone na oś \(x\)). Możemy to zapisać jako funkcję fragmentaryczną: \(\displaystyle f\left (x \right)=\left\ {\begin{array} {l} {{x}^{2}}-4\,\,\,\,\,\,\,\,\,\tekst{if} x< -2\text{ or }x> 2\\ – {{x}^{2}} \ text{+ 4}\,\,\,\,\,\,\text{if} -2 \ le x \ le 2 \ end{array} \right.\) widzimy, że to zapoczątkowało przekształconą funkcję kwadratową \(y={{x}^{2}}-4\) z wartością bezwzględną wokół niej, ponieważ wszystkie wartości \(y\) są dodatnie: \(y = \left| {{{x}^{2}}-4}\right|\).
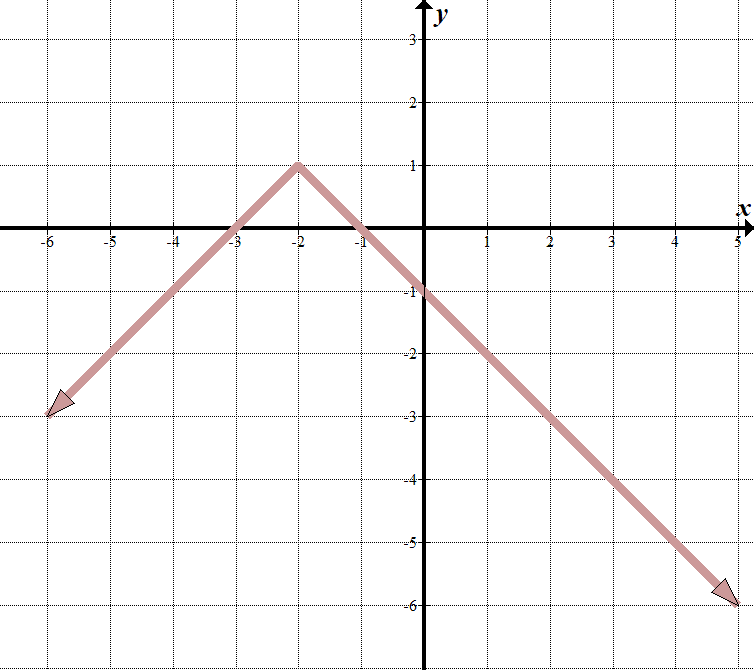	widzimy, że nasza „linia graniczna” znajduje się w \(x=-2\), więc to, co znajduje się wewnątrz znaku wartości bezwzględnej, musi być \(x+2\). Gdy \(x> -2\), widzimy, że równanie linii to \(y= – x-1\). Gdy \(x< -2\), linia jest \(y = x + 3\). Możemy to zapisać jako funkcję fragmentaryczną: \(\displaystyle f\left (x \right)=\left\ {\begin{array}{l} – x-1\,\,\,\,\,\,\text{if }x> -2\\x+3\,\,\,\,\,\,\,\,\,\,\text{if} x \ le -2 \ end{array} \right. prawdopodobnie łatwiej jest zapisać to jako przekształconą funkcję wartości bezwzględnej. Widzimy, że nadrzędna funkcja wartości bezwzględnej jest odwrócona pionowo, przesunięta w lewo o 2, a w górę o 1. Nasze równanie wartości bezwzględnej to \(y= – \ left / {x + 2} \right|\,\,+\,\,1\). To jest to samo, co funkcja fragmentaryczna powyżej. Spróbuj – to działa!

transformacje funkcji w kawałkach

zróbmy transformację funkcji w kawałkach. Dowiedzieliśmy się o funkcjach nadrzędnych i ich przekształceniach tutaj w sekcji wykresy i przekształcenia nadrzędne. Prawdopodobnie będziesz chciał najpierw przeczytać tę sekcję, zanim spróbujesz fragmentarycznej transformacji.

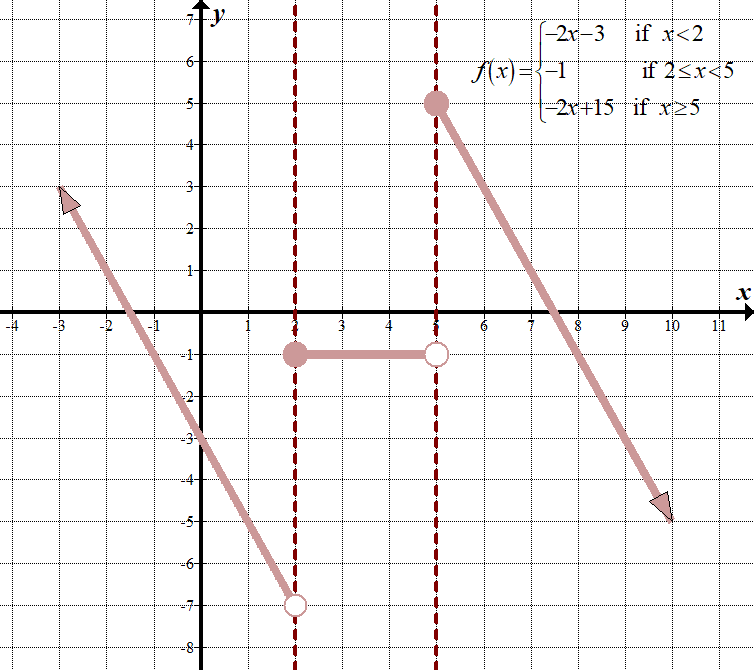
przekształćmy następującą funkcję fragmentaryczną obracającą się wokół osi \(x\), rozciągniętą pionowo o współczynnik 2 jednostek, 1 jednostkę w prawo i 3 jednostki w górę.

narysujemy \(-2F\left( x-1 \right)+3\), gdzie:

\(\displaystyle f \ left (x \right)=\left\ {\begin{align}x+4\,\,\,\,\,\,\,\,&\text{ if }x<&\text{ if 1 }\le x<4\\x-5\,\,\,\,\,\,\,\,& \ text {if} x\ge 4 \ end{align} \right.\)

upewnijmy się, że używamy punktów „granicznych”, gdy wypełniamy Wykres t dla transformacji. Pamiętaj, że przekształcenia wewnątrz nawiasów są wykonywane dla \(x\) (robiąc odwrotną matematykę), a na zewnątrz są wykonywane dla \(y\). Aby wymyślić Wykres t, jak pokazano w poniższej tabeli, możemy użyć kluczowych punktów, w tym dwóch punktów na każdej z „linii granicznych”.

zauważ, że ponieważ ta transformacja jest skomplikowana, możemy wymyślić nową funkcję piecewise, przekształcając 3 „kawałki”, a także przekształcając”\(x\) „S, gdzie punkty graniczne są (dodając 1 lub przechodząc do prawej 1), ponieważ wykonujemy odwrotną matematykę dla”\(x\) ” s. Aby otrzymać nowe funkcje w każdym przedziale, możemy po prostu zamienić „\(x-1\)” na „\(x\)” w oryginalnym równaniu, pomnożyć przez -2, a następnie dodać 3. Na przykład \(\displaystyle-2F\left( {x-1} \right)+3=-2\left+3=-2\left( {x+3} \right)+3=-2x-3\).

\(\displaystyle-2F\left ({x-1} \ right)+3 = \ left\ {\begin{array}{l} -2\left ({\left( {x-1} \right) + 4} \right)+3 = – 2x-3,\,\,\,\,\tekst{ if }x-1< 1\,\,\,\left ({x< 2} \right)\\-2\left (2 \right)+3=-1,\,\,\,\,\text{ if}\, \text{ 2 }\le x<5\\-2\left( {\left ({x-1} \right) -5} \right)+3 = – 2x+15,\,\,\,\,\text{ if} x\ge 5 \ end{array} \ right.

oto wykresy „przed” i „po”, w tym Wykres t:

Piecewise Parent Function	T-chart	Transformation of Function
\(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}x+4\,\,\,\,\,\,\,\,\text{if }x<1\\2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{if 1 }\le x<4\\x-5\,\,\,\,\,\,\,\,\text{if }x\ge 4\end{array} \right.\)	x + 1 x y –2y+3 1 0 4 –5 2 1 5 –7 2 1 2 –1 5 4 2 –1 5 4 –1 5 8 7 2 –1	\(\displaystyle -2f\left( {x-1} \right)+3=\left\{ \begin{array}{l}-2x-3\,\,\,\,\,\,\,\,\,\text{if }x<2\\-1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{if 2}\le x<5\\-2x+15\,\,\,\,\,\,\text{if }x\ge 5\end{array} \right.\)

Piecewise Function Word Problems

Problem:

Twój ulubiony ratownik psa pobiera opłaty w zależności od wagi Twojego psa. Jeśli twój pies ma 15 funtów i mniej, groomer pobiera 35 usd. Jeśli twój pies jest między 15 i 40 funtów, ona pobiera $40. Jeśli twój pies jest ponad 40 funtów, ona pobiera $40, plus dodatkowe $2 za każdy funt.

(a) Napisz funkcję opisującą, jakie opłaty pobiera twój pies.

(B) wykres funkcji.

(c) jakie opłaty pobierze groomer, jeśli twój uroczy piesek waży 60 funtów?

rozwiązanie:

(a) widzimy, że „punktami granicznymi” są 15 i 40, ponieważ są to wagi, w których zmieniają się ceny. Ponieważ mamy dwa punkty graniczne, będziemy mieli trzy równania w naszej funkcji fragmentarycznej. Musimy zacząć od 0, ponieważ psy muszą ważyć ponad 0 Funtów:

\(\displaystyle f\left (x \right)=\left\ {\begin{array} {l} \ text{ }……\,\,\,\,\,\,\,\,\,\text{if} 0<x\le 15\\ \ text{ }……\,\,\,\,\,\,\,\,\,\text{if }15<x\le 40\\ \ text{ }……\,\,\,\,\,\,\,\,\,\text{if} x> 40 \end{array} \ right.\)

szukamy „odpowiedzi” (ile kosztuje pielęgnacja) na „pytania” (Ile waży pies) dla trzech przedziałów cenowych. Pierwsze dwa są po prostu zryczałtowane opłaty ($35 i $ 40, odpowiednio). Ostatnie równanie jest trochę trudniejsze; groomer pobiera 40 $plus 2 $za każdy funt powyżej 40. Spróbujmy liczb rzeczywistych: jeśli twój pies waży 60 funtów, będzie pobierać 40 dolarów plus 2 razy \(20 (60-40)\). Zamienimy to w równanie: \(40+2 (x–40)\), które upraszcza się do \(2x-40\) (zobacz jak 2 jest nachyleniem?).

cała funkcja jest:

\(\displaystyle f\left (x \right)=\left\ {\begin{array} {l} \ text{ }35\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{if} 0<x\le 15\\ \ text{ }40\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{if} 15<x\le 40\\\text{ }40+2 \ left ({x-40} \right)\,\,\,\,\,\,\text{if} x> 40 \end{array} \ right.\ ) lub \(\displaystyle f\left (x \right)= \ left\ {\begin{array} {l} \ text{ }35\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{if} 0<x\le 15\\ \ text{ }40\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{if} 15<x\le 40\\ \ text{ }2x-40\,\,\,\,\,\,\,\text{if} x> 40 \end{array} \ right.

(b) narysujmy Wykres:zauważ, że to równanie jest nieciągłe. Zauważ również, że rozsądną domeną dla tego problemu może być \(\left ({0,200} \right]\) (biorąc pod uwagę, że psy nie ważą ponad 200 funtów!) i rozsądnym zakresem może być \(\left \ cup \left\).

(c) Jeśli twój pies waży 60 funtów, możemy użyć wykresu lub funkcji, aby zobaczyć, że będziesz musiał zapłacić $ 80. Whoa! To kosztuje więcej niż ludzkie strzyżenie (przynajmniej moje fryzury)!

Problem:

planujesz sprzedać koszulki She Love Math jako zbiórkę pieniędzy. Firma hurtowa t-shirt pobiera 10 USD za koszulkę za pierwsze 75 koszulek. Po zakupie pierwszych 75 koszulek do 150 koszulek firma obniży cenę do 7,50 USD za koszulkę. Po zakupie 150 koszulek cena spadnie do 5 USD za koszulkę. Napisz funkcję, która modeluje tę sytuację.

rozwiązanie:

widzimy, że „punktami granicznymi” są 75 i 150, ponieważ jest to liczba koszulek kupionych tam, gdzie zmieniają się ceny. Ponieważ mamy dwa punkty graniczne, będziemy mieli trzy równania w naszej funkcji fragmentarycznej. Zaczniemy od \(x\ge 1\), ponieważ zakładamy, że przynajmniej jedna koszulka jest kupiona. Uwaga w tym problemie liczba kupionych koszulek (\(x\)) lub domeny musi być liczbą całkowitą, ale to ograniczenie nie powinno mieć wpływu na wynik problemu.

\(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}\text{ }……\text {} 1\le x\le 75\\\text {}….. \text{ if }75<x\le 150\\\text {}….. \text{ if }X>150\end{array} \right.\)

szukamy „odpowiedzi” (całkowity koszt koszulek) na „pytania” (ile jest kupionych) dla trzech przedziałów cenowych.

dla maksymalnie 75 koszulek włącznie Cena wynosi 10$, więc całkowita cena będzie \(10x\). W przypadku ponad 75 koszulek, ale do 100 koszulek, koszt wynosi 7,50 USD, ale pierwsze 75 koszulek nadal będzie kosztować 10 USD za koszulkę. Druga funkcja obejmuje $ 750 wydane na pierwszych 75 koszulek (75 razy $10), a także zawiera $7.50 razy liczbę koszulek powyżej 75, co byłoby \((x-75)\). Na przykład, jeśli kupiłeś 80 koszulek, musisz wydać \(\$10 \ razy 75=\$750\), plus \(\$7.50 \ razy 5\,\) (80 – 75) na koszulki po 75.koszulce.

Podobnie, za ponad 150 koszul, zapłacilibyśmy jeszcze 10 dolarów w górę przez 75 koszul, 7 dolarów.50 Cena za 76 do 150 koszul (75 więcej koszul), a następnie 5 $za koszulę za liczbę kupionych koszul powyżej 150. Zapłacimy \(10(75)+7.50(75)+5(x-150)\) dla \(x\) koszulek. Umieść w liczbach i spróbuj!

cała funkcja to:

\(\displaystyle f\left (x \right)=\left\ {\begin{array}{l} \ text{ }10x\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{if} 1\le x \ le 75 \ \ \ text{ }7.5 x\text { } + \ text{ }187.5\,\,\,\,\,\text{if 7}5< x\le 150\\ \ text{ }5X+562.5\,\,\,\,\,\,\,\,\,\,\text{ if} x> 150\end{array} \right.\ ) lub \(\displaystyle f\left (x \right)= \ left\ {\begin{array} {l} \ text{ }10x\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{if} 1\le x \ le 75 \ \ \ text{ }7.5 x\text { } + \ text{ }187.5\,\,\,\,\,\text{if 7}5<x\le 150\\ \ text{ }5X+562.5\,\,\,\,\,\,\,\,\,\,\,\text{if} x> 150\end{array} \right.

Problem:

autobus kosztuje 50 $za pierwsze 400 mil, a każde dodatkowe 300 mil (lub ich ułamek) dodaje 10 $do taryfy.

Użyj funkcji fragmentarycznej do reprezentowania taryfy autobusowej pod względem odległości w milach.

rozwiązanie:

jest to rzeczywiście trudny problem, ale najpierw pomyślmy o „punkcie granicznym”, czyli 400. To całkiem proste, gdy jazda jest mniejsza niż 400 mil; koszt to $ 50.

dla większych niż 400 mil, musimy odjąć pierwsze 400 mil (ale pamiętaj, aby uwzględnić pierwsze 50$), podzielić liczbę mil pozostałych przez 300 mil (i zaokrąglić w górę, jeśli jest kwota ułamkowa) i pomnożyć to przez 10$.

najtrudniejsze jest to, że „zbieramy się” na Część następnych 300 mil. Możemy użyć funkcji „sufit” (oznaczonej przez \(\left\lceil {} \right\rceil\)); ta funkcja daje najmniejszą liczbę całkowitą, która jest większa lub równa jej wejściu; na przykład pułap zarówno 3.5, jak i 4 wynosi 4.

oto co mamy:

\(\displaystyle f\left (x \right)=\left\ {\begin{array} {l} \ text{ }50\text{ }\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{if} 0 \ le x \ le 400 \ \ text{ }50+10 \ times \ left \ lceil {\frac{{x-400}}{{300}}} \right\rceil \text{ }\,\,\,\,\,\,\text{ if} x>400\end{array} \right.

spróbujmy! Jeśli przejedziemy 1500 mil, koszt wyniesie \(\displaystyle 50+10 \ times \ left \ lceil {\frac{{1500-400}}{{300}}} \right\rceil \text {} = 50 + 10 \ times 4=\$90\).

Problem:

jaka wartość \(\boldsymbol{a}\) sprawi, że ta funkcja będzie ciągła?

\(\displaystyle f\left (x \right)=\left\ {\begin{array} {l}3 {{x}^{2}}+4\,\,\,\,\,\text{ if} x< -2\\5X+\boldsymbol{a}\,\,\,\,\,\,\,\,\text{if} x\ge -2 \ end{array} \right.

rozwiązanie:

aby funkcja była ciągła, w punkcie granicznym (gdzie Funkcja się zmienia), dwie wartości \(y\) muszą być takie same. Możemy podłączyć -2 dla \(x\) w obu funkcjach i upewnić się, że \(y\)’S są takie same

\(\begin{align}3 {{x}^{2}}+4 & = 5X + a\\3{{\left ({-2} \ right)}^{2}}+4&=5\left( {-2} \right)+a\\12+4&=-10+a\\a&=26\end{align}\)

Jeśli \(a=26\), funkcja jest ciąg dalszy!

poznaj te zasady i ćwicz, ćwicz, ćwicz!

Więcej praktyki: użyj widżetu Mathway poniżej, aby spróbować napisać funkcję fragmentaryczną. Kliknij Wyślij (niebieska strzałka po prawej stronie problemu) i kliknij Napisz wartość bezwzględną jako fragment, aby zobaczyć odpowiedź.

Możesz również wpisać swój problem lub kliknąć trzy kropki w prawym górnym rogu i kliknąć „przykłady”, aby zagłębić się w temat.

Jeśli klikniesz Stuknij, aby wyświetlić kroki, lub Kliknij tutaj, możesz zarejestrować się w Mathway na bezpłatną wersję próbną, a następnie przejść do płatnej subskrypcji w dowolnym momencie (aby rozwiązać dowolny problem matematyczny!).

na macierze i rozwiązywanie układów z macierzami – jesteś gotowy!