- cele nauki
- praca przeciw grawitacji
- konwersja pomiędzy energią potencjalną a energią kinetyczną
- wykorzystanie energii potencjalnej do uproszczenia obliczeń
- przykład 1. Siła zatrzymywania spadania
- Strategia
- rozwiązanie
- dyskusja
- przykład 2. Znalezienie prędkości kolejki górskiej z jej wysokości
- Strategia
- rozwiązanie dla części 1
- rozwiązanie dla części 2
- Dyskusja i implikacje
- nawiązywanie połączeń: badanie typu Take-Home—Konwersja potencjału na energię kinetyczną
- podsumowanie sekcji
- pytania koncepcyjne
- problemy& ćwiczenia
- Słowniczek
- wybrane rozwiązania problemów& ćwiczenia
cele nauki
pod koniec tej sekcji będziesz w stanie:
- wyjaśnić grawitacyjną energię potencjalną pod względem pracy wykonanej przeciwko grawitacji.
- Pokaż, że grawitacyjna energia potencjalna obiektu o masie m na wysokości h na Ziemi jest podana przez PEg = mgh .
- Pokaż jak można wykorzystać wiedzę o energii potencjalnej jako funkcji położenia do uproszczenia obliczeń i wyjaśnienia zjawisk fizycznych.
praca przeciw grawitacji
wspinanie się po schodach i podnoszenie przedmiotów to praca zarówno w sensie naukowym, jak i codziennym—to praca przeciw sile grawitacji. Kiedy jest praca, następuje przemiana energii. Praca wykonana przeciwko sile grawitacji przechodzi w ważną formę zmagazynowanej energii, którą zbadamy w tej sekcji.

Rysunek 1. (a) praca wykonana w celu podniesienia ciężaru jest przechowywana w układzie masa-Ziemia jako grawitacyjna energia potencjalna. (b) w miarę jak ciężar porusza się w dół, owa grawitacyjna energia potencjalna przenoszona jest do zegara z kukułką.
obliczmy pracę wykonaną przy podnoszeniu obiektu o masie m przez wysokość h, taką jak na rysunku 1. Jeśli obiekt jest podnoszony prosto do góry ze stałą prędkością, to siła potrzebna do jego podniesienia jest równa jego masie. Praca wykonana na masie jest wtedy W = FD = mgh . Definiujemy to jako grawitacyjną energię potencjalną (PEg) włożoną (lub uzyskaną przez) układ obiekt-Ziemia. Energia ta związana jest ze stanem separacji pomiędzy dwoma obiektami, które przyciągają się wzajemnie siłą grawitacji. Dla wygody określamy to jako kołek uzyskany przez obiekt, uznając, że jest to energia zmagazynowana w polu grawitacyjnym Ziemi. Dlaczego używamy słowa „system”? Energia potencjalna jest właściwością układu, a nie pojedynczego obiektu—ze względu na jego położenie fizyczne. Potencjał grawitacyjny obiektu wynika z jego położenia względem otoczenia w systemie Ziemia-obiekt. Siła przyłożona do obiektu jest siłą zewnętrzną, pochodzącą spoza Układu. Gdy działa dodatnio, zwiększa grawitacyjną energię potencjalną układu. Ponieważ energia potencjalna grawitacji zależy od względnego położenia, potrzebujemy poziomu odniesienia, na którym ustawimy energię potencjalną równą 0. Zazwyczaj wybieramy ten punkt jako powierzchnię ziemi, ale ten punkt jest arbitralny; ważna jest różnica w grawitacyjnej energii potencjalnej, ponieważ ta różnica odnosi się do wykonanej pracy. Różnica w grawitacyjnej energii potencjalnej obiektu (w układzie Ziemia-obiekt) między dwoma szczeblami drabiny będzie taka sama dla dwóch pierwszych szczebli jak dla dwóch ostatnich szczebli.
konwersja pomiędzy energią potencjalną a energią kinetyczną
grawitacyjna energia potencjalna może być zamieniona na inne formy energii, takie jak energia kinetyczna. Jeśli uwolnimy masę, siła grawitacji wykona na niej pracę równą mgh, zwiększając w ten sposób jej energię kinetyczną o tę samą ilość (zgodnie z twierdzeniem praca-energia). Bardziej użyteczne będzie rozważenie tylko konwersji PEg do KE bez wyraźnego rozważenia pośredniego etapu pracy. (Patrz Przykład 2.) Ten skrót ułatwia rozwiązywanie problemów za pomocą energii (jeśli to możliwe), a nie jawnie za pomocą sił.
dokładniej definiujemy zmianę potencjalnej energii grawitacyjnej ΔPEg jako ΔPEg = mgh, gdzie dla uproszczenia oznaczamy zmianę wysokości przez h, a nie zwykłą Δh. Zauważ, że h jest dodatnie, gdy wysokość końcowa jest większa niż Wysokość początkowa i odwrotnie. Na przykład, jeśli masa 0,500 kg zawieszona na zegarze z kukułką jest podniesiona 1.00 m, wtedy jego zmiana w energii potencjału grawitacyjnego wynosi
\begin{array}{lll}mgh&&(0.500\text{ kg})(9.80\text{ m/s}^2)(1.00\text{ m})\\\text{ }&&4.90\text{ kg}\cdot\text{m}^2\Text{/S}^2=4.90\text{ j}\end{array}\\
zauważ, że jednostki grawitacyjnej energii potencjalnej okazują się dżule, takie same jak w przypadku pracy i innych form energii. Gdy zegar biegnie, masa jest obniżana. Możemy myśleć, że masa stopniowo rezygnuje ze swoich 4.90 J grawitacyjnej energii potencjalnej, bez bezpośredniego uwzględnienia siły grawitacji, która wykonuje pracę.
wykorzystanie energii potencjalnej do uproszczenia obliczeń

Rysunek 2. Zmiana grawitacyjnej energii potencjalnej (ΔPEg) między punktami A i B jest niezależna od drogi.
równanie ΔPEg = mgh stosuje się dla każdej ścieżki, która ma zmianę wysokości h, nie tylko wtedy, gdy masa jest podniesiona prosto do góry. (Patrz Rysunek 2.) Znacznie łatwiej jest obliczyć mgh (proste mnożenie) niż obliczyć pracę wykonaną wzdłuż skomplikowanej ścieżki. Idea grawitacyjnej energii potencjalnej ma tę podwójną zaletę, że jest bardzo szeroko stosowana i ułatwia obliczenia.
od teraz rozważymy, że każdej zmianie pozycji pionowej H masy m towarzyszy zmiana grawitacyjnej energii potencjalnej mgh i unikniemy równoważnego, ale trudniejszego zadania obliczania pracy wykonanej przez siłę grawitacji lub przeciwko niej.
ΔPEg = mgh dla dowolnej ścieżki między dwoma punktami. Grawitacja jest jedną z małych klas sił, w której praca wykonywana przez siłę lub przeciwko niej zależy tylko od punktu początkowego i końcowego, a nie od ścieżki między nimi.
przykład 1. Siła zatrzymywania spadania
a 60.0-kg osoba skacze na podłogę z wysokości 3,00 m. jeśli wyląduje sztywno (ze stawami kolanowymi ściskającymi o 0,500 cm), Oblicz siłę na stawy kolanowe.
Strategia
energia tej osoby jest sprowadzana do zera w tej sytuacji dzięki pracy wykonanej na nim przy podłodze, gdy się zatrzymuje. Początkowy PEg przekształca się w KE, gdy upada. Praca wykonywana przez podłogę zmniejsza tę energię kinetyczną do zera.
rozwiązanie
praca wykonywana na osobie przy podłodze, gdy zatrzymuje się, jest podana przez w = FD cos θ = −Fd, ze znakiem minus, ponieważ przemieszczenie podczas zatrzymywania i siła z podłogi są w przeciwnych kierunkach (cos θ = cos 180º = -1). Podłoga usuwa energię z systemu, więc wykonuje negatywną pracę.
energia kinetyczna, którą osoba ma po dotarciu do podłogi, to ilość energii potencjalnej utraconej przez upadek z wysokości h: ke = −ΔPEg = −mgh.
odległość D, że zginanie kolan osoby jest znacznie mniejsza niż wysokość H upadku, więc dodatkowa zmiana grawitacyjnej energii potencjalnej podczas zginania kolan jest ignorowana.
praca wykonywana przez podłogę na osobie zatrzymuje osobę i przynosi jej energię kinetyczną do zera: W = −KE = mgh.
łączenie tego równania z wyrażeniem W daje −Fd = mgh.
przypominając, że h jest ujemne, ponieważ osoba upadła, siłę na stawy kolanowe podaje
\displaystyle{F}=-\frac{mgh}{d}=-\frac{\left(60.0\text{ kg}\right)\left(9.80\text{ m/s}^2\right)\left(-3.00\text{ m}\right)}{5.00\times10^{-3}\text{ m}}=3.53\times10^5\text{ N}\\
dyskusja
tak duża siła (500 razy większa niż waga osoby) w krótkim czasie uderzenia wystarczy, aby połamać kości. Znacznie lepszym sposobem na amortyzację wstrząsu jest zginanie nóg lub toczenie się po ziemi, zwiększając czas działania siły. Ruch zginający 0,5 m w ten sposób daje siłę 100 razy mniejszą niż w przykładzie. Skakanie kangura pokazuje tę metodę w działaniu. Kangur jest jedynym dużym zwierzęciem, które wykorzystuje hopping do poruszania się, ale szok w hopping jest amortyzowany przez zginanie tylnych nóg w każdym skoku. (Patrz Rysunek 3.)

Rysunek 3. Praca wykonana przez ziemię nad kangurem zmniejsza jego energię kinetyczną do zera, gdy ląduje. Jednak poprzez zastosowanie siły podłoża na tylnych nogach na dłuższą odległość, wpływ na kości jest zmniejszona. (źródło: Chris Samuel, Flickr)
przykład 2. Znalezienie prędkości kolejki górskiej z jej wysokości
- jaka jest końcowa prędkość kolejki pokazana na rysunku 4, jeśli zaczyna się od odpoczynku na szczycie wzgórza 20,0 m i praca wykonywana przez siły tarcia jest znikoma?
- jaka jest jego prędkość końcowa (ponownie zakładając znikome tarcie), jeśli jego prędkość początkowa wynosi 5,00 m/s?
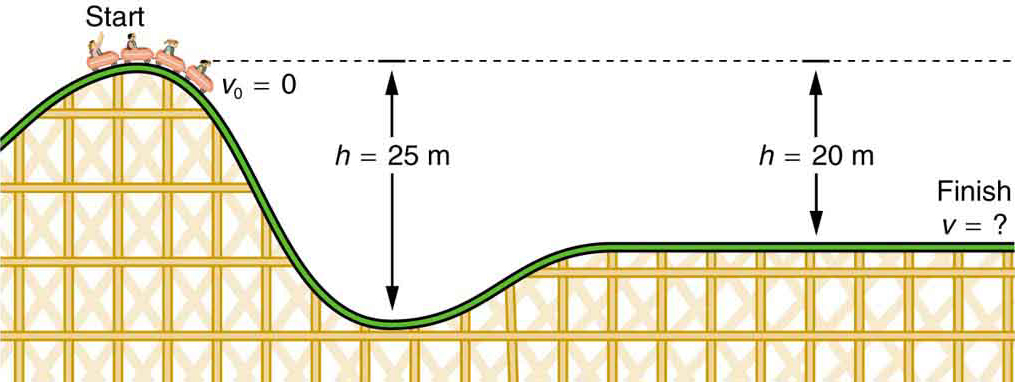
Rysunek 4. Prędkość kolejki górskiej wzrasta, gdy grawitacja ciągnie ją w dół i jest największa w najniższym punkcie. Patrząc pod względem energii, grawitacyjna energia potencjalna układu roller-Coaster-Earth jest przekształcana w energię kinetyczną. Jeśli praca wykonana przez tarcie jest znikoma, wszystkie ΔPEg są konwertowane na KE.
Strategia
kolejka górska traci energię potencjalną podczas zjazdu w dół. Zaniedbujemy tarcie, tak że pozostała siła wywierana przez Tor jest siłą normalną, która jest prostopadła do kierunku ruchu i nie działa. Praca netto na roller coaster jest następnie wykonywana przez samą grawitację. Utrata grawitacyjnej energii potencjalnej z ruchu w dół Przez odległość h równa się zyskowi energii kinetycznej. Można to zapisać w postaci równania jako-ΔPEg = ΔKE. Korzystając z równań dla PEg i KE, możemy rozwiązać końcową prędkość v, która jest żądaną ilością.
rozwiązanie dla części 1
tutaj początkowa energia kinetyczna wynosi zero, więc \Delta\text{KE}=\frac{1}{2}mv^2\\. Równanie zmiany energii potencjalnej stwierdza, że ΔPEg = mgh. Ponieważ h jest w tym przypadku ujemne, przepiszemy to jako ΔPEg = – mg / h/, aby wyraźnie pokazać znak minus. Zatem-ΔPEg = ΔKE staje się mg / h/= \ frac{1}{2} {mv}^2\\.
rozwiązując dla v, znajdujemy, że mass anuluje i że v=\sqrt{2G|h|}\\.
podstawiając znane wartości,
\begin{array}{lll}v&&\sqrt{2\left(9.80\text{ m/s}^2\right)\left(20.0\text{ m}\right)}\\\text{ }&&19.8\text{ m/s}\end{array}\\
rozwiązanie dla części 2
ponownie −δpeg = δke. W tym przypadku istnieje początkowa energia kinetyczna, więc
\Delta\text{KE}=\frac{1}{2}mv^2-\frac{1}{2}mv_0^2\\.
tak więc mg|h|=\frac{1}{2}mv^2-\frac{1}{2}mv_0^2\\.
przestawianie daje \frac{1}{2}mv^2=mg|h|+\frac{1}{2}mv+0^2\\.
oznacza to, że końcowa energia kinetyczna jest sumą początkowej energii kinetycznej i grawitacyjnej energii potencjalnej. Masa ponownie anuluje, A v = \sqrt{2G / h / +v_0^2}\\.
to równanie jest bardzo podobne do równania kinematycznego v=\sqrt{v_0^2+2AD}\\, ale jest bardziej ogólne—równanie kinematyczne jest ważne tylko dla stałego przyspieszenia, podczas gdy nasze równanie powyżej jest ważne dla dowolnej ścieżki niezależnie od tego, czy obiekt porusza się ze stałym przyspieszeniem. Teraz, podstawiając znane wartości daje
\begin{array}{lll}v&&\sqrt{2\left(9.80\text{ m/s}^2\right)\left(20.0\text{ m}\right)+\left(5.00\text{ m/s}\right)^2}\\\text{ }&&20.4\text{ m/s}\end{array}\\
Dyskusja i implikacje
najpierw zauważ, że mass anuluje. Jest to dość zgodne z obserwacjami poczynionymi w spadających obiektach, że wszystkie obiekty spadają w tym samym tempie, jeśli tarcie jest znikome. Po drugie, pod uwagę brana jest tylko prędkość kolejki górskiej; nie ma informacji o jej kierunku w żadnym punkcie. To ujawnia inną ogólną prawdę. Gdy tarcie jest znikome, prędkość spadającego ciała zależy tylko od jego początkowej prędkości i wysokości, a nie od jego masy lub obranej drogi. Na przykład kolejka górska będzie miała taką samą prędkość końcową, niezależnie od tego, czy spadnie 20,0 m prosto w dół, czy też obędzie bardziej skomplikowaną ścieżkę, jak ta na rysunku. Po trzecie, i być może nieoczekiwanie, ostateczna prędkość w części 2 jest większa niż w części 1, ale znacznie mniej niż 5,00 m/s. wreszcie, należy zauważyć, że prędkość można znaleźć na dowolnej wysokości po drodze, po prostu stosując odpowiednią wartość h w punkcie zainteresowania.
widzieliśmy, że praca wykonywana przez siłę grawitacji lub przeciwko niej zależy tylko od punktu początkowego i końcowego, a nie od ścieżki między nimi, co pozwala nam zdefiniować uproszczone pojęcie grawitacyjnej energii potencjalnej. Możemy zrobić to samo dla kilku innych sił i zobaczymy, że prowadzi to do formalnej definicji prawa zachowania energii.
nawiązywanie połączeń: badanie typu Take-Home—Konwersja potencjału na energię kinetyczną
w tym eksperymencie można badać konwersję grawitacyjnej energii potencjalnej na energię kinetyczną. Na gładkiej, równej powierzchni użyj linijki z rowkiem biegnącym wzdłuż jej długości i książki, aby wykonać nachylenie (patrz rysunek 5). Umieść marmur w pozycji 10 cm na linijce i pozwól jej się przewrócić. Gdy uderzy w poziomą powierzchnię, zmierz czas potrzebny na zrolowanie jednego metra. Teraz umieść marmur w pozycjach 20 cm i 30 cm i ponownie zmierz czas potrzebny na zrolowanie 1 m na płaskiej powierzchni. Znajdź prędkość marmuru na poziomej powierzchni dla wszystkich trzech pozycji. Wykreśl prędkość do kwadratu w stosunku do odległości przebytej przez marmur. Jaki jest kształt każdej działki? Jeśli kształt jest linią prostą, wykres pokazuje, że energia kinetyczna marmuru na dole jest proporcjonalna do jego energii potencjalnej w punkcie uwolnienia.

Rysunek 5. Marmur przewraca linijkę, a jej prędkość na poziomej powierzchni jest mierzona.
podsumowanie sekcji
- praca przeciw grawitacji w podnoszeniu obiektu staje się energią potencjalną układu obiekt-Ziemia.
- zmiana energii potencjalnej grawitacji, ΔPEg, wynosi ΔPEg = mgh, przy czym h oznacza wzrost wysokości, A G przyspieszenie spowodowane grawitacją.
- grawitacyjna energia potencjalna obiektu w pobliżu powierzchni Ziemi wynika z jego położenia w układzie masa-Ziemia. Jedynie różnice w energii potencjalnej grawitacji, ΔPEg, mają znaczenie fizyczne.
- gdy obiekt schodzi bez tarcia, jego potencjalna energia grawitacyjna zmienia się w energię kinetyczną odpowiadającą rosnącej prędkości, tak że ΔKE = −ΔPEg
pytania koncepcyjne
- w przykładzie 2 obliczyliśmy prędkość końcową kolejki górskiej, która zjechała na wysokość 20 m i miała prędkość początkową 5 m / s W Dół. Załóżmy, że kolejka górska miała początkową prędkość 5 m/s pod górę, a następnie zjechała pod górę, zatrzymała się, a następnie zjechała w dół do końcowego punktu 20 m poniżej startu. W takim przypadku okazało się, że miał taką samą prędkość końcową. Wyjaśnij w zakresie oszczędzania energii.
- czy praca, którą wykonujesz na książce, gdy podnosisz ją na półkę, zależy od obranej ścieżki? W czasie? Na wysokości półki? Na mszę św.?
problemy& ćwiczenia
- elektrownia wodna (patrz rysunek 6) zamienia grawitacyjną energię potencjalną wody za zaporą na energię elektryczną. (a) jaka jest grawitacyjna energia potencjalna względem generatorów jeziora o objętości 50.0 km3 (masa = 5,00 × 1013 kg), biorąc pod uwagę, że jezioro ma średnią wysokość 40,0 m Nad prądem? (B) Porăłwnaj to z energiÄ … zgromadzonÄ … w 9-megatonowej bombie fusion.

Rysunek 6. Elektrownia wodna (źródło: Denis Belevich, Wikimedia Commons)
- (a) ile energii potencjalnej grawitacji (w stosunku do ziemi, na której jest zbudowana) jest przechowywana w Wielkiej piramidzie Cheopsa, biorąc pod uwagę, że jej masa wynosi około 7 × 109 kg, a jej środek masy wynosi 36.5 m nad otaczającą ziemią? (b) jak ta energia jest porównywana z dziennym spożyciem pokarmu danej osoby?
- przypuśćmy, że 350-g Kookaburra (duży zimorodek) podnosi 75-g węża i podnosi go 2,5 m od ziemi na gałąź. a) ile pracy zrobił ptak na wężu? (b) ile pracy zrobił, aby podnieść swój własny środek masy do gałęzi?
- w przykładzie 2 odkryliśmy, że prędkość kolejki górskiej, która zjechała 20,0 m, była tylko nieco większa, gdy miała początkową prędkość 5,00 m / s niż gdy zaczynała od spoczynku. Oznacza to, że ΔPE >> KEi. Potwierdź to stwierdzenie, przyjmując stosunek ΔPE do KEi. (Należy pamiętać, że Msza odwołuje.)
- 100-g Samochodzik jest napędzany sprężyną, która uruchamia go w ruchu. Samochód podąża za zakrzywionym torem na rysunku 7. Pokaż, że ostateczna prędkość samochodu-zabawki wynosi 0,687 m/s, jeśli jego prędkość początkowa wynosi 2,00 m / s i pokonuje nachylenie bez tarcia, zyskując 0,180 m wysokości.

Rysunek 7. Samochodzik porusza się po pochyłym torze. (credit: Leszek Leszczyński, Flickr)
- w biegu zjazdowym zaskakująco mało zyskuje się na starcie biegu. (Wszakĺľe poczÄ … tkowa energia kinetyczna jest maĹ 'a w porăłwnaniu z przyrostem grawitacyjnej energii potencjalnej na nawet maĹ’ ych wzgăłrzach.) Aby to zademonstrować, znajdź prędkość końcową i czas potrzebny narciarzowi, który pokonuje 70,0 m na zboczu 30º: (a) zaczynając od odpoczynku. (B) zaczynając od prędkości początkowej 2,50 m/s. (c) czy odpowiedź Cię dziwi? Omów, dlaczego nadal korzystne jest uzyskanie startu w bardzo konkurencyjnych wydarzeniach.
Słowniczek
grawitacyjna energia potencjalna: energia, jaką obiekt posiada dzięki położeniu w polu grawitacyjnym
wybrane rozwiązania problemów& ćwiczenia
1. (a) 1,96 × 1016 J; (b) stosunek grawitacyjnej energii potencjalnej w jeziorze do energii zmagazynowanej w bombie wynosi 0,52. Oznacza to, że energia zmagazynowana w jeziorze jest o połowę mniejsza niż w 9-megatonowej bombie termojądrowej.
3. a) 1,8 J; B) 8,6 J
5. {v}_{F} = \sqrt{2GH+{v_0}^2}=\sqrt{2\left(9.80\text{ m/s}^2\right)\left(-0.180\text{ m}\right)+\left(2.00\text{ m/s}\right)^2}=0.687\text{ m/s}\\