po zrozumieniu funkcji wykładniczej, naszym następnym celem jest logarytm naturalny.

biorąc pod uwagę, jak logarytm naturalny jest opisany w podręcznikach matematycznych, niewiele jest w nim „naturalnego”: jest zdefiniowany jako odwrotność $e^x$, wystarczająco dziwny wykładnik.

ale jest świeże, intuicyjne Wyjaśnienie: logarytm naturalny daje czas potrzebny do osiągnięcia określonego poziomu wzrostu.

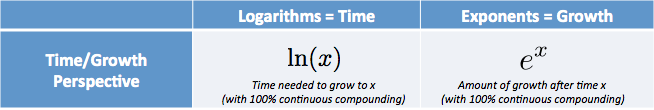
Załóżmy, że inwestujesz w żelki (kto nie?) ze stopą procentową 100% rocznie, stale rosnącą. Jeśli chcesz 10-krotnego wzrostu, zakładając ciągłe składanie, czekałbyś tylko $\LN(10)$ lub 2.302 lat. Nie widzisz, dlaczego potrzeba tylko kilku lat, aby uzyskać wzrost 10x? Nie widzisz, dlaczego wzór nie jest 1, 2, 4, 8? Czytaj więcej o e.

E i logarytm naturalny są bliźniacze:

• $e^x$ to ilość jaką mamy po rozpoczęciu od 1.0 i rosnący w sposób ciągły dla $X$ jednostek czasu
• $\ln(x)$ (logarytm naturalny) to czas, aby osiągnąć wartość $x$, zakładając, że stale wzrastaliśmy od 1.0

nie jest tak źle, prawda? Podczas gdy matematycy spierają się, aby dać ci długie, techniczne Wyjaśnienie, przejdźmy do intuicyjnego.

E oznacza wzrost

liczba e oznacza ciągły wzrost. Jak widzieliśmy ostatnio, $e^x$ pozwala nam połączyć szybkość i czas: 3 lata przy 100% wzroście jest tym samym, co 1 rok przy 300% wzroście, gdy jest stale powiększany.

możemy wziąć dowolną kombinację stawki i czasu (50% przez 4 lata) i przeliczyć stawkę na 100% dla wygody (dając nam 100% przez 2 lata). Przeliczając kurs na 100%, musimy tylko pomyśleć o składowej czasu:

intuicyjnie, $e^x$ oznacza:

• ile wzrostu dostanę po X jednostkach czasu (i 100% ciągłego wzrostu)
• na przykład: po 3 okresach czasu mam $e^3$ = 20,08 razy więcej „rzeczy”.

$e^x$ jest współczynnikiem skalowania, pokazującym nam ile wzrostu uzyskamy po $x$ jednostek czasu.

logarytm naturalny to czas

logarytm naturalny to odwrotność $e^x$, wymyślne określenie odwrotności. Mówiąc o fantazji, Łacińska nazwa to logarithmus naturali, co daje Skrót ln.

Co to oznacza?

• $e^x$ pozwala nam podłączyć czas i uzyskać wzrost.
• $\ln(x)$ pozwala nam podłączyć wzrost i uzyskać czas, który by to zajęło.

na przykład:

• $e^3$ to 20.08. Po 3 jednostkach czasu, kończymy z 20.08 razy więcej niż zaczęliśmy.
• $\ln (20.08)$ to około 3. Jeśli chcemy wzrostu 20,08, poczekamy 3 jednostki czasu(ponownie, zakładając 100% ciągły wzrost).

ze mną? Logarytm naturalny daje nam czas potrzebny do osiągnięcia pożądanego wzrostu.

arytmetyka logarytmiczna nie jest normalna

badałeś już logi i były to dziwne bestie. Jak zamienili mnożenie w dodawanie? Podział na odejmowanie? Zobaczmy.

Co to jest $\ln(1)$? Intuicyjnie, pytanie brzmi: jak długo mam czekać, aby uzyskać 1x moją aktualną kwotę?

Zero. Zip. Nic. Jesteś już na 1x aktualną kwotę! Wzrost z 1 do 1 nie wymaga czasu.

• $\ln(1) = 0$

ok, może Wartość ułamkowa? Jak długo, aby uzyskać 1/2 mojej obecnej kwoty? Zakładając, że stale wzrastasz w 100%, wiemy, że $\ln(2)$ to ilość czasu do podwojenia. Jeśli go odwrócimy (tzn. weźmiemy ujemny czas), będziemy mieli połowę naszej bieżącej wartości.

• $\ln(.5) = – \ln(2)= -.693$

ma sens, prawda? Jeśli się cofniemy .693 jednostki (powiedzmy ujemne sekundy) mielibyśmy połowę naszej bieżącej ilości. Ogólnie rzecz biorąc, możesz odwrócić ułamek i wziąć ujemny: $\ln (1/3) = – \ln(3) = -1.09$. Oznacza to, że jeśli cofniemy się o 1,09 jednostki czasu, będziemy mieli jedną trzecią tego, co mamy teraz.

Ok, a co z logarytmem naturalnym liczby ujemnej? Ile czasu zajmuje „wyhodowanie” kolonii bakterii z 1 do -3?

to niemożliwe! Nie można mieć „ujemnej” ilości bakterii, prawda? Co najwyżej (Eee … co najmniej) można mieć zero, ale nie ma sposobu, aby mieć ujemną ilość małych stworzeń. Ujemne bakterie nie mają sensu.

• $\LN(\text{negative number}) = \text{undefined}$

Undefined oznacza po prostu „nie ma czasu, który możesz poczekać”, aby uzyskać ujemną kwotę. (Cóż, jeśli użyjemy urojonych wykładników, istnieje rozwiązanie. Ale dziś bądźmy realni.)

mnożenie logarytmiczne to świetna zabawa

ile czasu zajmuje wzrost 9x aktualnej kwoty? Jasne, możemy po prostu użyć ln(9). Ale to zbyt proste, bądźmy inni.

możemy uznać wzrost 9x za potrojenie (biorąc $\ln(3)$ jednostek czasu), a następnie potrojenie ponownie(biorąc kolejne $\ln (3)$ jednostek czasu):

• czas rosnąć 9x = $\ln(9)$ = czas potroić i potroić ponownie = $\ln(3) + \ln(3)$

ciekawe. Każda liczba wzrostu, np. 20, może być uważana za wzrost 2x, a następnie wzrost 10x. Lub wzrost 4x, a następnie wzrost 5X. Lub wzrost 3x, a następnie wzrost 6,666 x. Widzisz wzór?

• $\ln(a*b) = \LN(a) + \ln(b)$

log a razy b = log(a) + log(B). Ten związek ma sens, gdy myślisz w kategoriach czasu na rozwój.

Jeśli chcemy wzrosnąć 30x, możemy poczekać $\ln(30)$ wszystkie na raz, lub po prostu poczekać $\ln(3)$, potroić, a następnie poczekać $\LN(10)$, aby ponownie wzrosnąć 10x. Efekt netto jest taki sam, więc czas netto powinien być taki sam (i jest).

a co z podziałem? $\ln (5/3)$ oznacza: jak długo trwa wzrost 5 razy, a następnie 1/3 tego?

cóż, Wzrost 5 razy to $\ln (5)$. Rosnąca 1/3 to $-\ln(3)$ jednostki czasu. Więc

• $\ln(5/3) = \ln(5) – \ln(3)$

, który mówi: rosnąć 5 razy i „cofnąć się w czasie”, aż będziesz miał jedną trzecią tej kwoty, więc pozostaniesz z 5/3 wzrostu. Ogólnie mamy

• $\ln(a/b) = \ln(a) – \ln(b)$

mam nadzieję, że Dziwna matematyka logarytmów zaczyna mieć sens: mnożenie wzrostu staje się dodawaniem czasu, podział wzrostu staje się odejmowaniem czasu. Nie zapamiętaj zasad, zrozum je.

używając naturalnych logów z dowolną szybkością

„jasne”, mówisz ” ten log działa na 100% wzrost, ale co z 5%, które normalnie dostaję?”

to żaden problem. „Czas”, który otrzymujemy z $\LN ()$ jest w rzeczywistości kombinacją szybkości i czasu, „x”z naszego równania $e^x$. Po prostu Zakładamy 100%, aby to uprościć, ale możemy użyć innych liczb.

Załóżmy, że chcemy 30x wzrostu: podłącz $\ln(30)$ i otrzymaj 3.4. Oznacza to:

• $e^x = \text{growth}$
• $e^{3.4} = 30$

i intuicyjnie to równanie oznacza „100% zwrotu za 3,4 roku to 30x wzrost”. Równanie możemy uznać za:

możemy modyfikować „rate” I „time”, o ile rate * time = 3.4. Załóżmy na przykład, że chcemy 30-krotnego wzrostu-jak długo czekamy zakładając 5% zwrotu?

• $\ln(30) = 3.4$
• $\text{rate} * \text{time} = 3.4$
• $.05 * \text{time} = 3.4$
• $\text{time} = 3.4 / .05 = 68 \text{years}$

intuicyjnie myślę, że „$\ln(30) = 3,4$, więc przy 100% wzroście zajmie to 3,4 roku. Jeśli podwoję tempo wzrostu, zmniejszę o połowę potrzebny czas.”

• 100% przez 3,4 lat = 1,0 * 3,4 = 3,4
• 200% przez 1,7 lat = 2,0 * 1,7 = 3,4
• 50% przez 6,8 lat = 0,5 * 6,8 = 3,4
• 5% przez 68 lat = .05 * 68 = 3.4

fajne, co? Dziennik naturalny może być używany z dowolną stopą procentową lub czasem, o ile ich produkt jest taki sam. Możesz poruszać zmiennymi, ile chcesz.

niesamowity przykład: reguła 72

reguła 72 jest skrótem matematycznym do oszacowania czasu potrzebnego na podwojenie Twoich pieniędzy. Wyprowadzimy go (yay!), a nawet lepiej, zrozumiemy to intuicyjnie.

ile czasu zajmuje podwojenie Twoich pieniędzy przy 100% odsetkach?

Uh oh. Używamy logarytmu naturalnego dla stałych stawek, ale teraz prosisz o roczne odsetki? Czy to nie zepsuje naszej formuły? Tak, ale przy rozsądnych stopach procentowych, takich jak 5%, 6%, a nawet 15%, nie ma dużej różnicy między rocznymi składanymi i w pełni ciągłymi odsetkami. Więc szorstki wzór działa, uh, mniej więcej i będziemy udawać, że otrzymujemy w pełni ciągłe zainteresowanie.

teraz pytanie jest proste: jak długo podwoić przy 100% odsetkach? ln (2) = .693. Trzeba .693 jednostki czasu (lata, w tym przypadku), aby podwoić swoje pieniądze z ciągłego compounding ze stawką 100%.

Ok, a co jeśli nasze zainteresowanie nie jest 100% co jeśli jest to 5% lub 10%?

proste. Tak długo, jak rate * time = .693, podwoimy nasze pieniądze:

• rate * time = .693
• time = .693 / Oceń

więc gdybyśmy mieli tylko 10% wzrostu, zajęłoby to .693 / .10 albo 6,93 lat do podwojenia.

aby uprościć rzeczy, pomnóżmy przez 100, abyśmy mogli mówić o 10, a nie .10:

• czas do podwojenia = 69.3 / stawka, gdzie przyjmuje się, że stawka jest w procentach.

teraz czas na podwojenie przy wzroście 5% wynosi 69,3 / 5 lub 13,86 lat. Jednak 69,3 nie jest najbardziej podzielną liczbą. Wybierzmy najbliższego sąsiada, 72, który można podzielić przez 2, 3, 4, 6, 8 i wiele innych liczb.

• czas podwoić = 72/Oceń

czyli reguła 72! Spokojnie.

Jeśli chcesz znaleźć czas na potrojenie, użyjesz ln(3) ~ 109.8 i uzyskasz

• czas na potrojenie = 110/Oceń

, co jest kolejną użyteczną zasadą. Zasada 72 jest przydatna dla stóp procentowych, wzrostu populacji, hodowli bakterii i wszystkiego, co rośnie wykładniczo.

gdzie stąd?

mam nadzieję, że logarytm naturalny ma większy sens — mówi o czasie potrzebnym na dowolną ilość wzrostu wykładniczego. Uważam to za” naturalne”, ponieważ e jest uniwersalną stopą wzrostu, więc ln można uznać za” uniwersalny ” sposób na określenie, ile czasu zajmuje wzrost.

Kiedy zobaczysz $\ln(x)$, pomyśl tylko „ile czasu potrzeba, aby urosnąć do x”. W następnym artykule połączymy e i ln, a słodki aromat matematyki wypełni powietrze.

dodatek: logarytm naturalny E

Szybki quiz: co to jest $\ln(e)$?

• Robot matematyczny mówi: ponieważ są zdefiniowane jako funkcje odwrotne, wyraźnie $\ln(e) = 1$
• intuicyjny człowiek: ln (e) to czas potrzebny na otrzymanie jednostek wzrostu” e ” (około 2.718). Ale e jest wielkością wzrostu po 1 jednostce czasu, więc $\ln(E) = 1$.

myśl intuicyjnie.

inne posty z tej serii

1. intuicyjny przewodnik po funkcjach wykładniczych& e
2. Demystyfikacja logarytmu naturalnego (ln)
3. wizualny przewodnik po prostych, złożonych i ciągłych stopach procentowych
4. wspólne definicje e (pokolorowane)
5. zrozumienie wykładników (dlaczego 0^0 = 1?)
6. używanie logarytmów w świecie rzeczywistym
7. Jak myśleć z wykładnikami i Logarytmami
8. zrozumienie dyskretnego vs. ciągłego wzrostu
9. co tak naprawdę oznacza wykładnik?
10. p: Dlaczego e jest wyjątkowy? (2.718… nie 2, 3.7 czy inna liczba?)