w innych sekcjach wspomniano, że wiele właściwości ciał stałych, cieczy i gazów można by uwzględnić, zakładając, że substancje są zbudowane z atomów lub cząsteczek, które są stale w ruchu. Prawo Boyle ’ a i inne prawa gazowe dały nam teraz znacznie więcej informacji ilościowych na temat gazów i warto zapytać, czy w poprzednim modelu możemy przewidywać ilościowo w zgodzie z tymi prawami. Odpowiadając na to pytanie, uzyskamy również ważny wgląd w naturę temperatury i energii cieplnej.

mikroskopowa teoria zachowania się gazu oparta na ruchu molekularnym nazywana jest kinetyczną teorią gazów. Jej podstawowe postulaty są wymienione w tabeli 1:

TABLE \(\PageIndex{1}\) postulaty kinetycznej teorii gazów.

1 cząsteczki w gazie są małe i bardzo daleko od siebie. Większość objętości, którą zajmuje gaz, to pusta przestrzeń.

2 cząsteczki gazu są w ciągłym, losowym ruchu. Tak samo wiele cząsteczek porusza się w jednym kierunku, jak w każdym innym.

3 cząsteczki mogą zderzać się ze sobą i ze ścianami pojemnika. Zderzenia ze ścianami odpowiadają za ciśnienie gazu.

4 gdy dochodzi do zderzeń, cząsteczki nie tracą energii kinetycznej; to znaczy, że zderzenia są doskonale elastyczne. Całkowita energia kinetyczna wszystkich cząsteczek pozostaje stała, chyba że istnieje jakaś zewnętrzna interferencja z

5 cząsteczki nie wywierają na siebie żadnych atrakcyjnych lub odpychających sił, z wyjątkiem procesu zderzenia. Pomiędzy zderzeniami poruszają się po liniach prostych.

z nich można uzyskać następującą ekspresję ciśnienia gazu pod względem właściwości jego cząsteczek:

\ Gdzie P, V = ciśnienie i objętość gazu

N = liczba cząsteczek

m = masa każdej cząsteczki

(u2)Ave = średnia (lub średnia) kwadratów wszystkich indywidualnych prędkości cząsteczkowych. Ta średnia prędkość kwadratowa musi być użyta, ponieważ ciśnienie jest proporcjonalne do kwadratu prędkości cząsteczkowej, A zderzenia cząsteczkowe powodują, że różne cząsteczki mają zupełnie różne prędkości.

zamiast zajmować się procedurą wyprowadzania Eq. \ (\ref{1}\), sprawdźmy równanie i przekonajmy się, że jego ogólne cechy są takie, jakich byśmy się spodziewali. Pod pewnymi względami, umiejętność robienia tego za pomocą formuły jest bardziej przydatna niż umiejętność jej wyprowadzania. Rysunek \(\PageIndex{1}\)

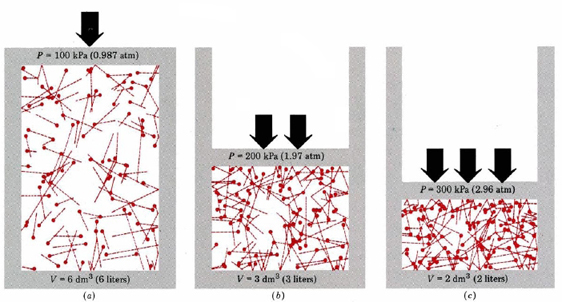po pierwsze, równanie mówi nam, że ciśnienie gazu jest proporcjonalne do liczby cząsteczek podzielonych przez objętość. Jest to pokazane graficznie na rysunku \(\PageIndex{1}\), Gdzie komputer narysował tę samą liczbę cząsteczek gazu zajmujących każdą z trzech różnych objętości. „Ogon” na każdej cząsteczce pokazuje dokładną ścieżkę, po której podążała ta cząsteczka w poprzedniej mikrosekundzie—im dłuższy ogon, tym szybciej cząsteczka szła. Średnia kwadratów długości ogona jest proporcjonalna do (u2) ave i jest taka sama we wszystkich trzech diagramach. Zakłada się również, że wszystkie cząsteczki mają równe masy.

jak widać, zmniejszenie objętości gazu zwiększa liczbę kolizji na jednostkę powierzchni na ścianach pojemnika. Każda kolizja wywiera siłę na ścianę; siła na jednostkę powierzchni jest ciśnieniem, a więc liczba kolizji na jednostkę powierzchni jest proporcjonalna do ciśnienia. Zmniejszenie o połowę objętości podwaja ciśnienie, co jest zgodne z eksperymentalnymi faktami podsumowanymi w prawie Boyle ’ a. Równanie \ (\ref{1}\) mówi również, że ciśnienie jest proporcjonalne do masy każdej cząsteczki gazu. Ponownie, tego byśmy się spodziewali. Ciężkie cząsteczki dają większe „pchnięcie” (technicznym określeniem jest to impuls) do ściany niż lekkie o tej samej prędkości.

wreszcie równanie mówi nam, że ciśnienie jest proporcjonalne do średniej kwadratów prędkości cząsteczkowych. Ta zależność od kwadratu prędkości jest rozsądna, jeśli zdamy sobie sprawę, że podwojenie prędkości cząsteczki ma dwa skutki.

Po pierwsze, cząsteczka może poruszać się dalej w określonym czasie, podwajając liczbę kolizji ze ścianami. To podwoiłoby ciśnienie. Po drugie, podwojenie prędkości cząsteczki podwaja popychanie lub impuls każdego zderzenia. To znowu podwaja ciśnienie. Dlatego podwojenie prędkości cząsteczki czterokrotnie zwiększa ciśnienie, a dla dużej liczby cząsteczek, P jest proporcjonalne do średniej prędkości kwadratowej.