orbitale atomowe
orbital jest kwantowym mechanicznym udoskonaleniem orbity Bohra. W przeciwieństwie do jego koncepcji prostej orbity kołowej o stałym promieniu, orbity są matematycznie wyprowadzonymi obszarami przestrzeni o różnych prawdopodobieństwach posiadania elektronu.
jeden ze sposobów reprezentowania rozkładów prawdopodobieństwa elektronów został zilustrowany na rysunku 6.5.2 dla orbitalu 1s wodoru. Ponieważ Ψ2 daje prawdopodobieństwo znalezienia elektronu w danej objętości przestrzeni (np. Pirometr sześcienny), Wykres Ψ2 względem odległości od jądra (r) jest wykresem gęstości prawdopodobieństwa. Orbital 1s jest sferycznie symetryczny, więc prawdopodobieństwo znalezienia elektronu 1s w dowolnym punkcie zależy tylko od jego odległości od jądra. Gęstość prawdopodobieństwa jest największa przy r = 0 (w jądrze) i maleje wraz ze wzrostem odległości. Przy bardzo dużych wartościach r gęstość prawdopodobieństwa elektronów jest bardzo mała, ale nie zerowa.
w przeciwieństwie do tego, możemy obliczyć radialne prawdopodobieństwo (prawdopodobieństwo znalezienia elektronu 1s w odległości r od jądra) przez zsumowanie prawdopodobieństwa elektronu znajdującego się we wszystkich punktach na serii X kulistych powłok o promieniu r1, R2, R3,…, rx − 1, rx. W efekcie dzielimy atom na bardzo cienkie koncentryczne powłoki, podobnie jak warstwy cebuli (część (a) na rysunku \(\PageIndex{1}\)) i obliczamy prawdopodobieństwo znalezienia elektronu na każdej kulistej powłoce. Przypomnijmy, że gęstość prawdopodobieństwa elektronu jest największa w r = 0 (część (B) na rysunku \(\PageIndex{1}\)), więc gęstość kropek jest największa dla najmniejszych kulistych muszli w części (a) na rysunku \(\PageIndex{1}\). Natomiast pole powierzchni każdej kulistej powłoki jest równe 4nr2, która rośnie bardzo szybko wraz ze wzrostem r (część (c) na rysunku \(\PageIndex{1}\)). Ponieważ pole powierzchni kulistych powłok zwiększa się szybciej wraz ze wzrostem r niż gęstość prawdopodobieństwa elektronów maleje, Wykres prawdopodobieństwa radialnego ma maksimum w określonej odległości (część (d) na rysunku \(\PageIndex{1}\)). Co najważniejsze, gdy r jest bardzo mały, pole powierzchni kulistej powłoki jest tak małe, że całkowite prawdopodobieństwo znalezienia elektronu blisko jądra jest bardzo niskie; w jądrze prawdopodobieństwo elektronu znika (część (D) na rysunku \(\PageIndex{1}\)).

dla atomu wodoru szczyt na wykresie prawdopodobieństwa radialnego występuje w r = 0,529 Å (52,9 pm), co jest dokładnie promieniem obliczonym przez Bohra dla orbity n = 1. Tak więc najbardziej prawdopodobny promień uzyskany z mechaniki kwantowej jest identyczny z promieniem obliczonym przez mechanikę klasyczną. W modelu Bohra przyjęto jednak, że elektron znajduje się w tej odległości w 100% czasu, podczas gdy w modelu mechaniki kwantowej Schrödingera znajduje się w tej odległości tylko przez pewien czas. Różnica między tymi dwoma modelami wynika z falopodobnego zachowania elektronu i zasady nieoznaczoności Heisenberga.
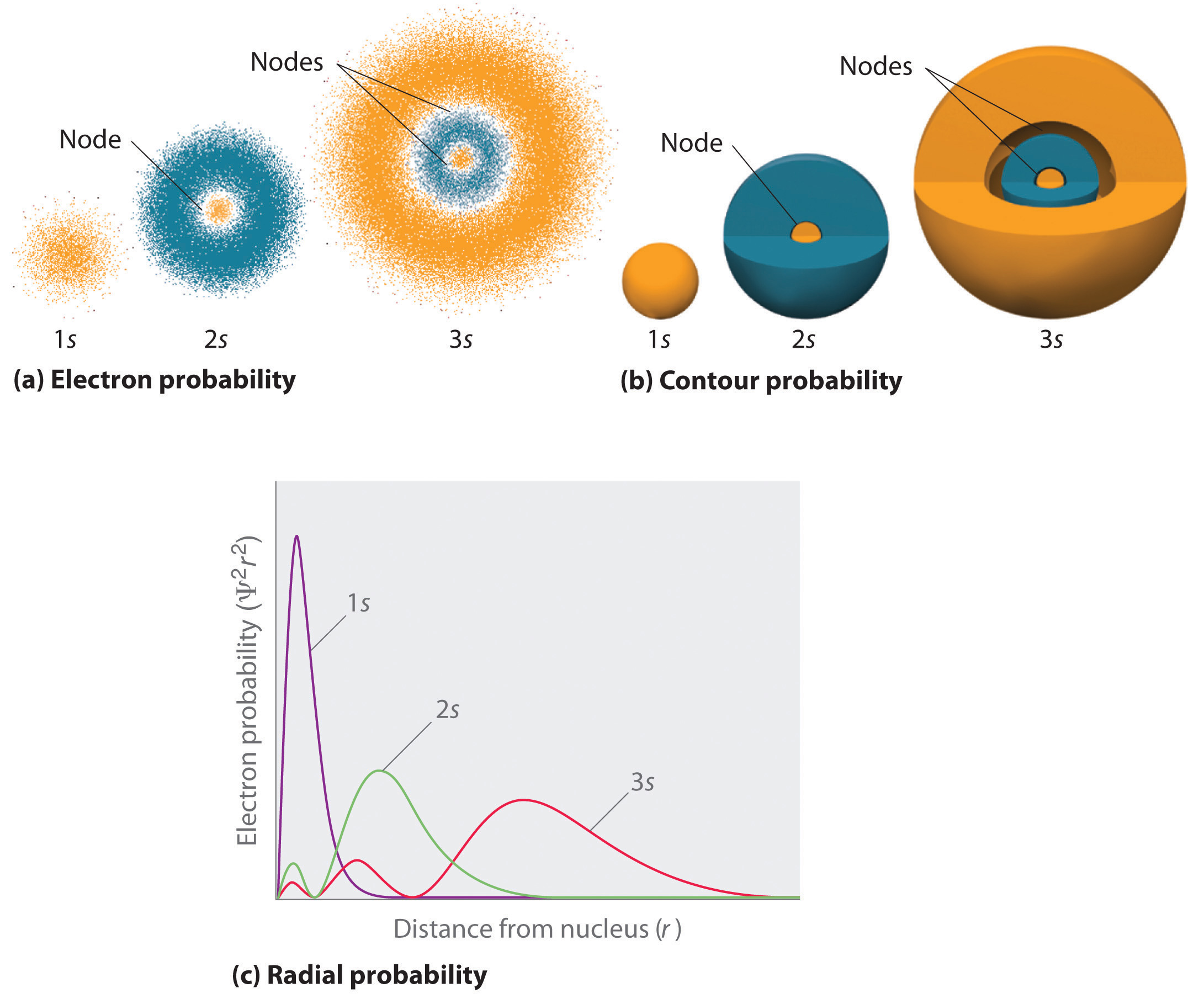
rysunek \(\PageIndex{2}\) porównuje gęstości prawdopodobieństwa elektronów dla orbitali wodoru 1s, 2s i 3S. Zauważ, że wszystkie trzy są sferycznie symetryczne. Jednak dla orbitali 2S i 3S (a także dla wszystkich innych orbitali s) gęstość prawdopodobieństwa elektronu nie spada płynnie ze wzrostem r. zamiast tego obserwuje się serię minimów i maksimów w promieniowych wykresach prawdopodobieństwa (część (c) na rysunku \(\PageIndex{2}\)). Minima odpowiadają węzłom sferycznym (regionom o zerowym prawdopodobieństwie elektronowym), które przeplatają się z regionami sferycznymi o niezerowym prawdopodobieństwie elektronowym.