Purplemath
i matematikk er en «identitet» en ligning som alltid er sann. Disse kan være «trivielt» sanne, som «x = x» eller nyttig sant, som Pythagorasetningen er «a2 + b2 = c2» for høyre trekanter. Det er mange trigonometriske identiteter, men følgende er de du mest sannsynlig vil se og bruke.
Basic & Pythagorean, Angle-Sum & -Difference, Double-Angle, Half-Angle, Sum, Product
Content Continues Below
MathHelp.com
Need a custom math course?
K12 | College | Test Prep

affiliate
legg merke til hvordan en «co-(noe)» trig-forholdet er alltid gjensidig av noe «ikke-co» – forhold. Du kan bruke dette faktum for å hjelpe deg å holde rett at cosecant går med sinus og secant går med cosinus.
følgende (spesielt den første av de tre nedenfor) kalles «Pythagoranske» identiteter.
sin2(t) + cos2(t) = 1
tan2(t) + 1 = sec2(t)
1 + cot2(t) = csc2(t)
Annonse
Merk at de tre identitetene fremfor alt involverer kvadrering og tallet 1. Du kan se Pythagorean-Thereom forholdet klart hvis du vurderer enhetssirkelen, hvor vinkelen er t, den «motsatte» siden er sin (t) = y, den «tilstøtende» siden er cos (t) = x, og hypotenusen er 1.
tan(–t) = –tan(t)
sin(–t) = –sin(t)
tan (–t) = -tan(t)
Legg spesielt merke til at sinus og tangent er merkelige funksjoner, er symmetriske om opprinnelsen, mens cosinus er en jevn funksjon, er symmetrisk om opprinnelsen, mens cosinus er en jevn funksjon, som er symmetrisk om opprinnelsen.y-aksen. Det faktum at du kan ta argumentets» minus » tegn utenfor (for sinus og tangent) eller eliminere det helt (for cosinus) kan være nyttig når du arbeider med kompliserte uttrykk.
Vinkel-Sum-og -Forskjellen Identiteter
sin(α + β) = sin(α) cos(β) + cos(α) sin(β)
sin(α – β) = sin(α) cos(β) – cos(α) sin(β)
cos(α + β) = cos(α) cos(β) – sin(α) sin(β)
cos(α – β) = cos(α) cos(β) + sin(α) sin(β)
forresten, i over identiteter, vinklene er merket med greske bokstaver. A-bokstaven, «α», kalles «alpha», som er uttalt»AL-fuh». B-bokstaven, «β», kalles «beta», som er uttalt»BAY-tuh».
Innholdet Fortsetter Under
Dobbelvinklede Identiteter
sin(2x) = 2 sin(x) cos(x)
Cos(2x) = cos2(x)-sin2(x) = 1 – 2 sin2(x) = 2 cos2(x) – 1
Halv –
de ovennevnte identitetene kan angis på nytt ved å kvadrere hver side og doble alle vinkelmålingene. Resultatene er som følger:
Affiliate

Sum Identities
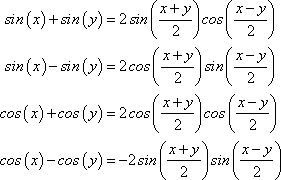
Product Identities
affiliate
du skal bruke alle disse identitetene, eller nesten så, for å bevise andre trig identiteter og for å løse trig ligninger. Men hvis du fortsetter å studere kalkulator, vær særlig oppmerksom på de omarbeidede sinus-og cosinus halvvinkelidentitetene, fordi du bruker dem mye i integrert kalkulator.
URL: https://www.purplemath.com/modules/idents.htm