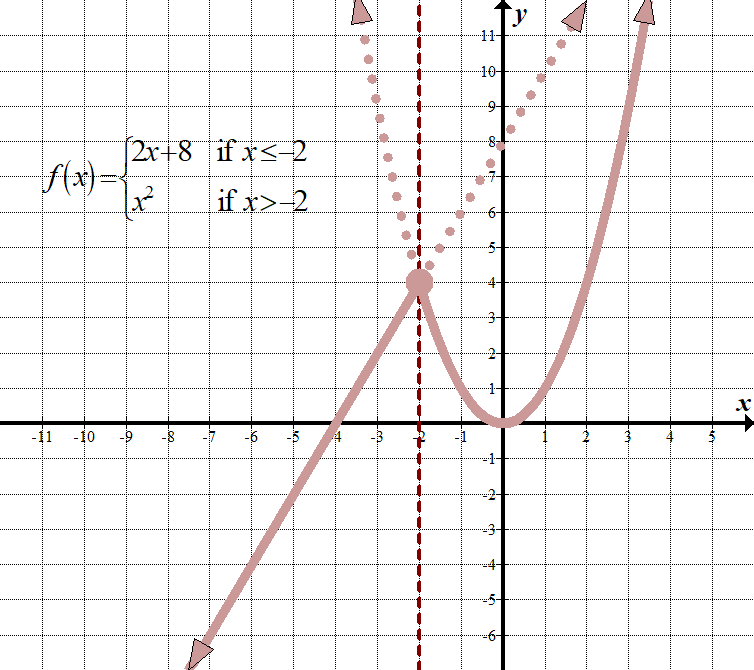denne delen dekker:

Introduksjon Til Piecewise Funksjoner

Evaluere Piecewise Funksjoner

Grafer Piecewise Funksjoner

Hvordan Fortelle om En Piecewise Funksjon Er Kontinuerlig eller Ikke-Kontinuerlig

Å Skaffe Ligninger Fra Piecewise Funksjonsgrafer

Absoluttverdi Som En Piecewise Funksjon

Transformasjoner Av Piecewise Funksjoner

Piecewise Funksjon Ordproblemer

Mer Praksis

stykkevis Funksjoner (eller stykkevis funksjoner) Er Akkurat Det De Heter: stykker av forskjellige funksjoner (underfunksjoner) alt på en graf. Den enkleste måten å tenke på dem er hvis du tegnet mer enn en funksjon på en graf, og du slettet bare deler av funksjonene der de ikke skal være (langs \(x\) ‘ s); de er definert annerledes for forskjellige intervaller av \(x\). \(y\) er definert forskjellig for forskjellige verdier av \ (x\); vi bruker \(x\) for å se opp hvilket intervall det er i, slik at vi kan finne ut hva \(y\) skal være.

Merk at det er et eksempel på en stykkevis funksjons inverse her i Inverses Of Functions-delen.

Here’s an example and graph:

Piecewise Function

Graph

\(\displaystyle f\left( x \right)=\left\{ \begin{align}2x+8\,\,\,\,\,&\text{ if }x\le -2\\{{x}^{2}}\,\,\,\,\,\,\,\text{ }\,&\text{ if }x>-2\end{align} \right.\) (Det finnes andre måter å vise dette på, for eksempel å bruke en «for» i stedet for en «hvis», og bruke komma eller semikolon i stedet for «hvis».) Domene: \(\mathbb{R},\,\,\,\tekst{eller}\,\,\venstre( {-\infty ,\infty } \høyre)\) Område: \(\mathbb{R},\,\,\,\tekst{eller}\,\, \venstre ({- \infty, \infty}\høyre)\)

hva dette betyr er for hver\ (x\) mindre enn eller lik -2, må vi tegne linjen\ (2x+8\), som om det var den eneste funksjonen på grafen. For hver \(x\) verdi større enn -2, må vi graf \({{x}^{2}}\), som om det var den eneste funksjonen på grafen. Da må vi «kvitte oss med» de delene vi ikke trenger. Husk at vi fortsatt bruker opprinnelsen som referansepunkt for begge grafer!

Se hvordan den vertikale linjen \(x=-2\) fungerer som en» grense » linje mellom de to grafene?

Merk at punktet \((-2,4)\) har en lukket sirkel på den. Teknisk sett bør den bare tilhøre \(2x+8\) – funksjonen, siden den funksjonen har mindre enn eller likhetstegn, men siden punktet også er på\ ({{x}^{2}}\) grafen, kan vi bare bruke en lukket sirkel som om den vises på begge funksjonene. Se, ikke så ille, ikke sant?

Evaluere Piecewise Funksjoner

Noen ganger vil du bli gitt stykkevis funksjoner og bedt om å evaluere dem; med andre ord, finn\ (y\) verdiene når du får en \ (x\) verdi. La oss gjøre dette for \(x=-6\) og \(x=4\) (uten å bruke grafen). Her er funksjonen igjen:

\(\displaystyle f\left (x \ right)=\left\{ \begin{align}2x+8\,\,\,\,\,&\tekst{ if }x \ le -2 \ \ {{x}^{2}}\,\,\,\,\,\,\,\text { }\, &\text{ if }x>-2 \ end{align} \ right.\)

vi vil først se på forholdene til høyre først for å se hvor vår \(x\) er. Når \(x=-6\), vet vi at det er mindre enn -2, så vi plugger inn vår \(x\) til \(2x+8\) bare. \(f (x)\) eller \ (y\) er \((2)(-6)+8=-4\). Vi bryr oss ikke engang om \(\boldsymbol{{x}^{2}}\)! Så enkelt er det. Du kan også se at vi gjorde dette riktig ved å bruke grafen ovenfor.

prøv nå \(x=4\). Vi ser på høyre først, og ser at vår \(x\) er større enn -2, så vi plugger den inn i \({{x}^{2}}\). (Vi kan bare ignorere \(2x + 8\) denne gangen.) \(f (x)\) eller \ (y\) er \({{4}^{2}}=16\).

Grafer Stykkevis Funksjoner

du vil sannsynligvis bli bedt om å graf stykkevis funksjoner. Noen ganger vil grafene inneholde funksjoner som ikke er kontinuerlige eller diskontinuerlige, noe som betyr at du må hente blyanten midt i grafen når du tegner den (som et hopp!). Kontinuerlige funksjoner betyr at du aldri trenger å plukke opp blyanten hvis du skulle tegne dem fra venstre til høyre.

og husk at grafene er sanne funksjoner bare hvis de passerer Den Vertikale Linjetesten.

la oss tegne disse stykkevis funksjonene og avgjøre om de er kontinuerlige eller ikke-kontinuerlige. Legg merke til hvordan vi tegner hver funksjon som om den var den eneste, og deretter «slette» delene som ikke er nødvendig. Vi får Også Domenet og Rekkevidden som vi gjorde her i Algebraiske Funksjoner-delen.

Piecewise Function	Graph
\(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}-2x+8\,\,\,\,\,\,\text{if }x\le 4\\\frac{1}{2}x-2\,\,\,\,\,\,\,\,\,\text{if }x>4\end{array} \right.\) Continuous Domain: \(\mathbb{R},\,\,\,\text{or}\,\,\left( {-\infty ,\infty } \right)\) Range: \(\left( {0,\infty } \right)\)
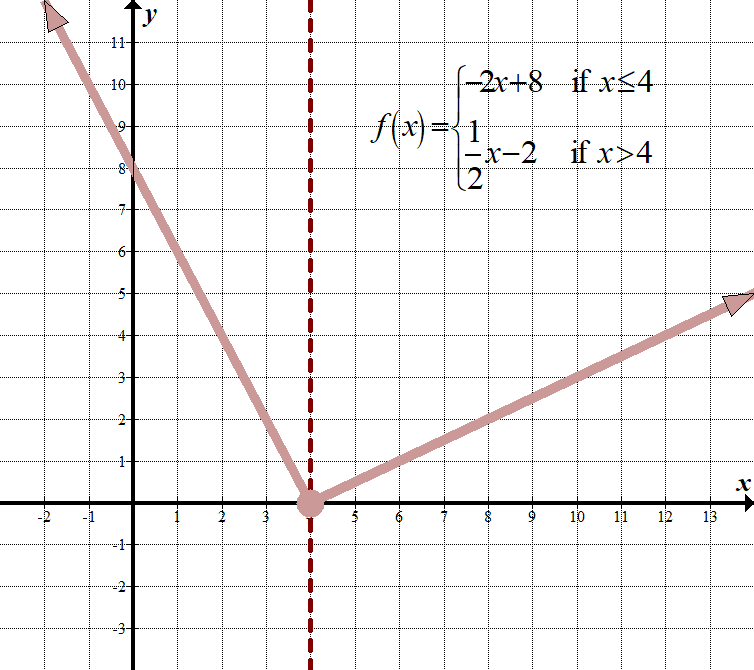\(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}x+4\,\,\,\,\,\,\,\,\,\text{if }x<1\\2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{if 1}\le x<4\\x-5\,\,\,\,\,\,\,\,\,\text{if }x\ge 4\end{array} \right.\) Non-Continuous Domain: \(\mathbb{R},\,\,\,\text{or}\,\,\left( {-\infty ,\infty } \right)\) Range: \(\mathbb{R},\,\,\,\text{or}\,\,\left( {-\infty ,\infty } \right)\)

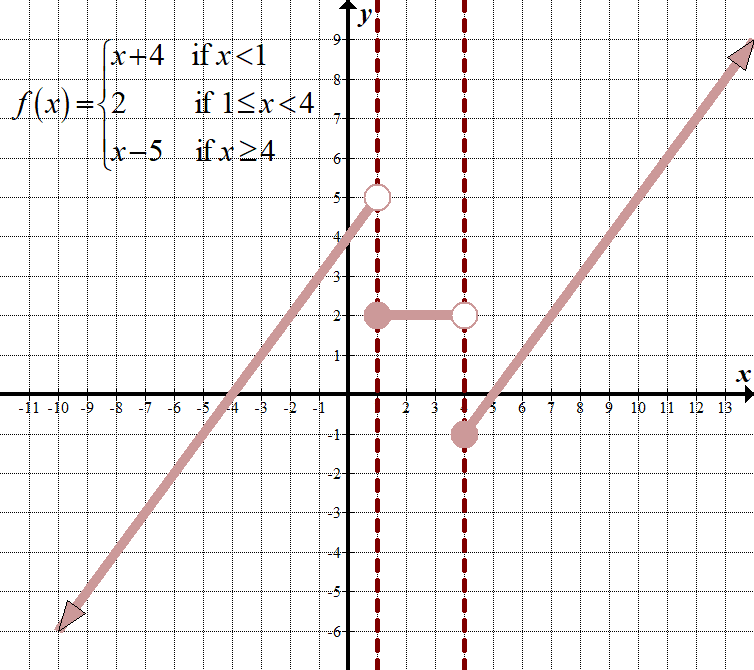We can actually put piecewise functions in the graphing calculator:

Piecewise Function Screens

Steps and Notes

Enter the piecewise function on three lines: her er grafen:

for å sette stykkevis funksjon \(\displaystyle f\venstre( x \høyre)=\venstre\{ \begin{array{l} x+4\,\,\,\,\,\,\,\,\,\tekst{if }x<1\\2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\tekst{if 1 }\le x<4 \ \ -5 + x\,\,\,\,\,\tekst{if }x\ge 4 \ end{array} \ høyre.\ ) i kalkulatoren kan du skrive inn funksjonen på tre linjer ved å dele funksjonen i hvert intervall med en» test ulikhet » av det intervallet (og se parenteser!). grunnen til at vi deler med intervaller eller ulikheter er fordi kalkulatoren vil returnere en 1 hvis ulikheten (som \(x<1\)) er sant; for eksempel vil \((x+4)\) bare ende opp \((x+4)/(1)\) når \(x<1\). Når \(x \ ge 1\), deler vi med 0, så ingenting blir trukket. Her er hva vi kan sette i kalkulatoren: \(\displaystyle \begin{array}{l}{{Y}_{1}}=\venstre( {x+4} \høyre)/\venstre( {x<1} \høyre)\\{{y}_{2}}=\venstre( 2 \høyre)/\venstre( {x\ge 1\tekst{ og }x<4} \høyre)\\{{y}_{3}}=\venstre( {-5+x} \høyre)/\venstre( {x\ge 4} \høyre)\end{array}\) (merk at du også kan skrive inn dette på en linje ved å multiplisere betingelsene i stedet for å dele, og bruke plusstegn mellom hver av de tre funksjonene/intervaller: \(\displaystyle {{Y}_{1}}=\venstre( {x+4} \høyre)\venstre( {x<1} \høyre)+\venstre( 2 \høyre)\venstre( {x\ge 1\tekst{ og }x<4} \høyre)+\venstre( {-5+x} \høyre)\venstre( {x\ge 4} \høyre)\).) her er tastetrykkene for å bruke tre linjer. Merk at du bruker 2ND MATH (TEST) for å komme til skjermen som har \(\le \), \(\ge \) og så videre. For eksempel får 2nd MATH 6 deg \(\le \). Bruk 2ND MATH (TEST), rett TIL LOGIKK, deretter 1, for» og » i \({{Y} _ {2}}\).

Slik Forteller Du Om Stykkevis funksjon Er Kontinuerlig eller Ikke-Kontinuerlig

for å fortelle om en stykkevis graf er kontinuerlig eller ikke-kontinuerlig, kan du kan se på grensepunktene og se om \(y\) punktet er det samme på hver av dem. (Hvis \(y\)’s var annerledes, ville det være et «hopp» i grafen!)

La oss prøve dette for funksjonene vi brukte ovenfor:

Piecewise Function	Check Boundary Points
\(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}-2x+8\,\,\,\,\,\,\,\text{if }x\le 4\\\frac{1}{2}x-2\,\,\,\,\,\,\,\,\,\,\text{if }x>4\end{array} \right.\)	Let’s check \(x=4\) in both parts of the function, since 4 is the «boundary point”: \(\beginn{array}{l}-2(4)+8=0\\\,\,\,\frac{1}{2}(4)-2=0\end{array}\) siden \(0=0\) er denne stykkevis funksjonen kontinuerlig.
\(\displaystyle f\venstre( x \høyre)=\venstre\{ \beginn{array}{l}x+4\,\,\,\,\,\,\,\,\,\,\,\,\,\tekst{if }x<1\\2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\tekst{if 1 }\le x<4 \ \ -5 + x\,\,\,\,\,\,\,\,\,\tekst{if }x\ge 4 \ end{array} \ høyre.\)	la oss sjekke inn de to første delene av funksjonen. Merk i den andre delen er \(y\) alltid 2: \(\beginn{array}{l}1+4=5\\\,\,\,\,\,\,\,\,\,2=2\end{array}\) siden \(5\ne 2\), kan vi stoppe her, og merk at denne stykkevis funksjonen ikke er kontinuerlig. Hvis \(y\)’s var like, måtte vi gå en for å sjekke neste grensepunkt på \(x=4\).

Innhenting Av Ligninger fra Stykkevis Funksjonsgrafer

du kan bli bedt om å skrive en stykkevis funksjon, gitt en graf. Nå som vi vet hva stykkevis funksjoner handler om, er det ikke så ille!

hvis du vil se hvordan du får ligninger fra lineære grafer, kan Du Se Få Ligningene Til En Linje, og fra kvadratikker, kan Du Se Finne En Kvadratisk Ligning Fra Punkter eller En Graf.

her er grafene, med forklaringer på hvordan å utlede sine stykkevis ligninger:

Piecewise Function Graph	Procedure to get Function
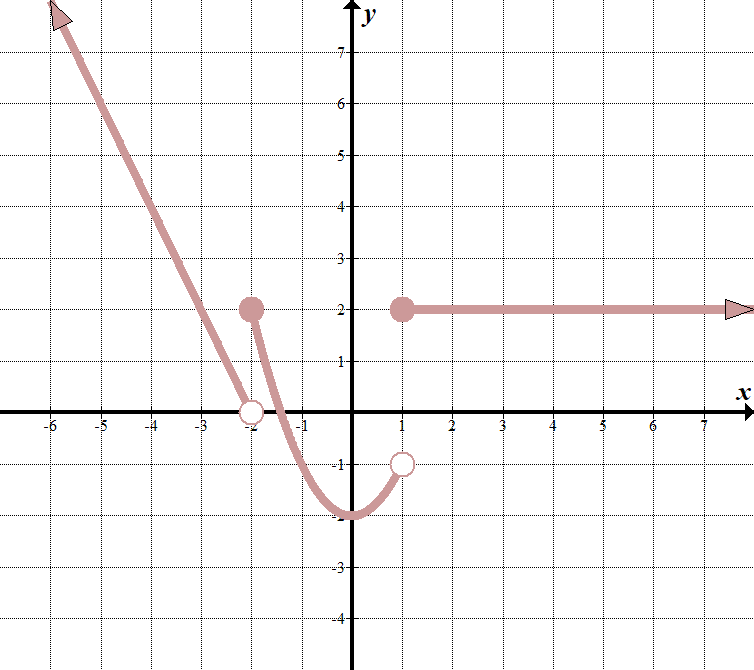	We see that our «boundary lines” are at \(x=-2\) and \(x=1\). We know that our function will look something like this (notice open and closed endpoints): \(\displaystyle f\venstre( x \høyre)= \ venstre\ {\begin{array}{l} \ tekst{ }……\,\,\,\,\,\,\,\,\tekst{if }x <-2 \ \ \ tekst{ }……\,\,\,\,\,\,\,\,\tekst{if} – \ tekst{2 } \ le x <1 \ \ \ tekst{ }……\,\,\,\,\,\,\,\,\tekst {if }x \ ge 1 \ end{array} \ høyre.\) Vi kan velge to punkter \((-2,0)\) og \((-3,2)\) på venstre linje for å få ligningen \(y= – 2x-4\). den midterste funksjonen er \(y={{x}^{2}}-2\), og den høyre funksjonen er bare den horisontale linjen \(y=2\). dermed er piecewise-funksjonen: \(\displaystyle f\venstre( x \høyre)= \ venstre\ {\begin{array}{l} – 2x-4\,\,\,\,\,\,\,\tekst{if }x<-2\\ \ tekst{ }{{x}^{2}}-2\,\,\,\,\,\,\,\,\,\,\tekst{if} – \ tekst{2} \ le x <1 \ \ \ tekst{ 2}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\tekst {if }x \ ge 1 \ end{array} \ høyre.\)
	vi ser at vår «grenselinje» er på \(x=5\). Siden linjene møtes på \((5,4)\), spiller det ingen rolle hvor vi legger \(\le\) eller \(\ge\) tegnet; vi kan bare ikke sette det begge steder, eller det ville ikke være en funksjon. Vi har så langt: \(\displaystyle f\left (x \ right)= \ left \ {\begin{array}{l} \ text{ }……\,\,\,\,\,\,\,\,\,\tekst{if }x<5 \ \ \ tekst{ }……\,\,\,\,\,\,\,\,\,\tekst{if }x \ ge 5 \ end{array} \ høyre.\) Igjen må vi se på hver linje separat for å bestemme deres ligninger. Vi kan enten ta 2 poeng fra hver linje for å få disse, eller utlede fra bakker og \(y\– – avskjærer; stykkevis funksjon er: \(\displaystyle f\venstre (x \ høyre)=\venstre\{ \begin{array}{l}\frac{6}{5}x-2\,\,\,\,\,\,\,\tekst{if }x<5 \ \ \ frac{2}{5}x+2\,\,\,\,\,\,\,\tekst{if }x \ ge 5 \ end{array} \ høyre.\)

Absoluttverdi som En Stykkevis Funksjon

vi kan skrive absoluttverdifunksjoner som stykkevis funksjoner – det er veldig kult! Du vil kanskje vurdere Å Løse Absolutte Verdiligninger og Ulikheter før du fortsetter videre til dette emnet.

La oss si at vi har funksjonen \(f \ left (x \right)= \ left / x \ right|\). Fra det vi lærte tidligere, vet vi at når \(x\) er positiv, siden vi tar absoluttverdien, vil den fortsatt bare være \(x\). Men når \(x\) er negativ, når vi tar absoluttverdien, må vi ta motsatt (negere det), siden absoluttverdien må være positiv. Fornuftig? Så, for eksempel, hvis vi hadde \(/5/\), tar vi bare det som er inne i absolutt tegn, siden det er positivt. Men for \(/-5/\) må vi ta motsatt (negativt) av hva som er inne i absoluttverdien for å gjøre det \(\displaystyle 5\,\,\,(-\,-5=5)\).

Dette betyr at vi kan skrive denne absoluttverdifunksjonen som en stykkevis funksjon. Legg merke til at vi kan få «vendepunktet » eller» grensepunktet » ved å sette det som er inne i absoluttverdien til 0. Da bruker vi enten den opprinnelige funksjonen, eller negerer funksjonen, avhengig av funksjonens tegn (uten absolutt verdi) i det intervallet.

for eksempel kan vi skrive \(\displaystyle \ left / x \ right / \ text { } = \ left\ {\begin{array}{l}x\,\,\,\,\,\,\,\,\,\tekst{if }x \ ge 0 \ \ – x\,\,\,\,\,\tekst{if }x < 0 \ end{array} \ høyre.\). Vær også oppmerksom på at hvis funksjonen er kontinuerlig (det er ingen «hopp») ved grensepunktet, spiller det ingen rolle hvor vi legger «mindre enn eller lik» (eller «større enn eller lik») tegn, så lenge vi ikke gjentar dem! Vi kan ikke gjenta dem fordi vi teoretisk ikke kan ha to verdier av \(y\) for det samme \ (x\), eller vi ville ikke ha en funksjon.

Here are more examples, with explanations. (You might want to review Quadratic Inequalities for the second example below):

Absolute Value Function	Method to get Piecewise Function
\(g\left( x \right)=\left| {2x+3} \right|\)	Let’s first find the «boundary line”. Vi gjør dette ved å sette hva som er inne i absoluttverdien til 0, og deretter løse for \(\boldsymbol{x}\). når \(2x + 3 \ ge 0\), får vi \(\displaystyle x \ ge – \ frac{3}{2}\) (faktisk kan vi beholde \(\ge \) når vi løser). Når \(2x + 3\) er positiv, tar vi det bare «som det er», men hvis det er negativt, må vi negere hele greia. derfor er stykkevis-funksjonen: \(\displaystyle \venstre / {2x+3} \høyre / = \ venstre\ {\begin{array}{l}2x+3\,\,\,\,\,\,\,\,\,\tekst {if }x \ ge – \ frac{3}{2} \ tekst { } \ \ – 2x-3\,\,\,\,\,\tekst{if }x < -\frac{3}{2}\end{array} \høyre.\) Prøv det-det fungerer!
\(f\left( x \right)=\left| {{{x}^{2}}-4} \right|\)	la oss først finne «grenselinjen(e)»; vi setter hva som er inne i absoluttverdien til 0. når \({{x}^{2}}-4\ge 0\), får vi \(x\le -2\) eller \ (x\ge 2\) (prøv noen tall!). Når \({{x}^{2}}-4\) er positiv, tar vi det bare «som det er», men hvis det er negativt, må vi negere det. piecewise-funksjonen er: \(\displaystyle \venstre / {{{x}^{2}}-4} \høyre / = \ venstre\ {\begin{array}{l}{{x}^{2}}-4\,\,\,\,\,\tekst{if }x \ le -2 \ \ 4 – {{x}^{2}}\,\,\,\,\,\tekst{if }-2<x<2 \ \ {{x}^{2}}-4\,\,\,\,\,\tekst {if }x\ge 2 \ tekst { } \ end{array} \ høyre.\ ) eller \ (\displaystyle \ venstre / {{{x}^{2}}-4} \ høyre / = \ venstre\ {\begin{array}{l}{{x}^{2}}-4\,\,\,\,\,\,\tekst {if }x\le -2 \ tekst { }\,\, \ tekst{eller}\,\, \ tekst{ }x \ ge 2 \ \ 4 – {{x}^{2}}\,\,\,\,\,\,\,\tekst{if }-2<x<2\end{array} \høyre.\) Igjen (siden funksjonen er kontinuerlig), spiller det ingen rolle hvor vi har \(\le\) og \(\ge\) (i motsetning til\ (<\) og\ (>\)), så lenge vi ikke gjentar dem.	\(f\left( x \right)=2x+\left|{x+2} \right/\)	dette er litt vanskeligere, siden vi har en \(x\) innenfor og utenfor absoluttverdien. For «grenselinjen» bruker vi bare det som er inne i absoluttverdien. når \(x+2 \ ge 0\), får vi \(x\ge -2\). Men for stykkevis funksjon må vi bruke hele funksjonen, inkludert delen som er utenfor absoluttverdien. Så, den stykkevis funksjon er: \(\displaystyle 2x+\venstre / {x+2} \høyre / = \ venstre\ {\begin{array}{l}2x + x+2\,\,\,\,\,\tekst{if }x \ ge -2 \ \ 2x-x-2\,\,\,\,\,\tekst{if }x <-2 \ end{array} \ høyre.\ ) la oss forenkle: \(\displaystyle 2x+\venstre|{x+2} \høyre / =\venstre\{ \begin{array}{l}3x+2\,\,\,\,\,\,\,\tekst {if }x \ ge -2 \ \ x-2\,\,\,\,\,\,\,\,\,\,\tekst{if }x <-2 \ end{array} \ høyre.\ ) Prøv noen verdier mindre enn og flott da -2; de burde fungere!	\(g\venstre( x \høyre)=\venstre| {{{x}^{2}}-4x-5} \høyre|\)	denne løses best med et tegndiagram siden vi har en kvadratisk og vi trenger å vite hvor funksjonen er positiv og negativt. først faktor kvadratisk inne i absoluttverdien funksjonen til \(\venstre ({x-5} \ høyre) \ venstre ({x + 1} \høyre)\). Bruk deretter et tegndiagram for å se hvor faktorene er positive og negative, og husk at hvor faktorene er positive, bruker vi funksjonen «som den er», og hvor faktorene er negative, negerer vi funksjonen: \(\displaystyle \venstre|{{{x}^{2}}-4x-5} \høyre / =\venstre\{ \begin{array}{l}{{x}^{2}}-4x-5\,\,\,\,\,\,\,\,\,\,\,\,\,\,\tekst{if }x \ le -1\,\,\,\,\tekst{eller}\,\,\,\, x \ ge 5 \ \ – \ venstre ({{x}^{2}} – 4x-5} \ høyre)\,\,\,\,\tekst{if }-1<x<5 \ tekst { } \ end{array} \ høyre.\ )	\(\displaystyle g\venstre( x \høyre)=\frac{{\venstre| {x+2} \høyre|}}{{x+2}}\)	dette er en rasjonell funksjon, siden det er en variabel i nevnen. når \(x+2 \ ge 0\), får vi \(\displaystyle x \ ge -2\). Når \(x + 2\) er positiv, tar vi det bare «som det er», men hvis det er negativt, må vi negere hva som er i absoluttverdien: \(\displaystyle \ frac {{\left / {x+2} \right/}} {{x + 2}}=\left\{ \begin{array}{l}\frac{{x + 2}}{{x+2}}\,\,\,\,\,\,\,\,\,\tekst {if }x\ge -2\\\frac {{- x-2}}{{x+2}}\,\,\,\,\,\,\tekst{if }x <-2 \ end{array} \ høyre.\). Men vi må være forsiktige, siden \(x\ne 2\) (domenebegrensning: nevneren ville være 0). derfor er stykkevis-funksjonen: \(\displaystyle \ frac {{\venstre / {x+2} \ høyre/}} {{x + 2}}= \ venstre\ {\begin{array}{l}1\,\,\,\,\,\,\,\,\,\,\tekst{if }x >-2\\-1\,\,\,\,\,\,\tekst{if }x <-2 \ end{array} \ høyre.\).

Du kan også bli bedt om å ta en absolutt verdi graf og skrive den som en stykkevis funksjon:

Absolute Value Graph	Method to get Piecewise Function
	We see that our «boundary line” is at \(x=0\), so what’s inside the absolute value sign must be \(x\) or a factor of \(x\). (Dette skyldes at for å få grenselinjen med en absolutt verdifunksjon, setter vi hva som er inne i absoluttverdien til 0, og løser for \(x\)). når \(x> 0\), kan vi se at likningen av linjen er \(y=2x-2\). Når \(x < 0\), er ligningen \(y=2x-2\). Vi kan skrive dette som en stykkevis funksjon: \(\displaystyle f\left( x \right)= \ left \ {\begin{array}{l}2x-2\,\,\,\,\,\,\,\tekst{if }x >0\\-2x-2\,\,\, \ tekst{if }x \ le 0 \ end{array} \ høyre.\) Vi kan også skrive dette som en transformert absoluttverdifunksjon: \(y=2\left| x \right / -2\) eller \(y= \ left / {2x} \ right / -2\) (siden 2 er positiv, kan den være innenfor eller utenfor \(\left / { \ ,\,} \ right/\)). (Dette er fornuftig siden når det som er inne i \(\left| {\,\,} \right|\) er \(> 0\), bruker vi den vanlige funksjonen \(y=2x-2\), og når det som er inne i er \(< 0\), negerer vi absolutt verdidelen for å gjøre det \(y=-\left( {2x} \høyre)-2\)).
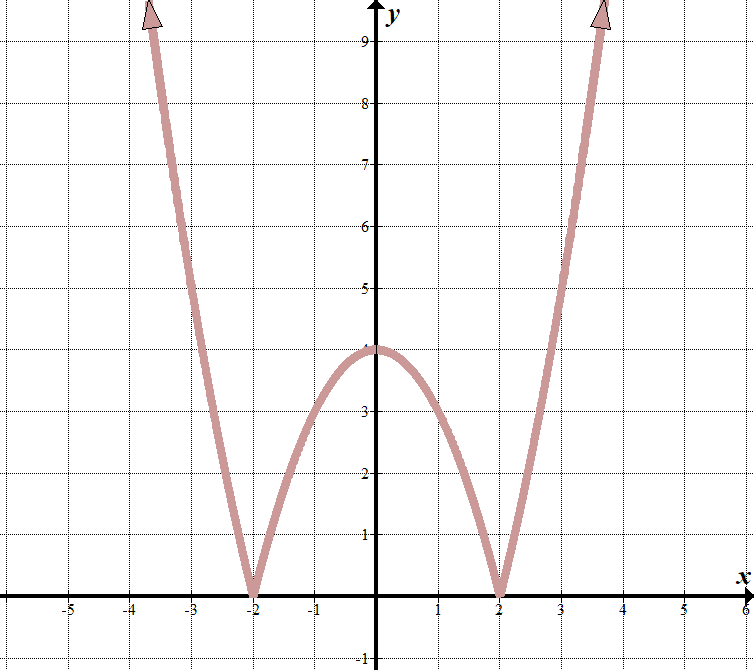	vi ser at våre «grenselinjer» er på \(x=2\) og \(x=-2\), så hva som er inne i absoluttverditegnet må ha faktorer av \(x-2\) og \(x+2\). når \(x< -2\) eller \ (x > 2\), kan vi se at grafen ser ut som den normale delen av grafen \(y={{x}^{2}}-4\). (Jeg fant ut dette ved å kjenne faktorene, og ta et godt gjetning!) Når \(-2 < x < 2\), blir ligningen vendt eller negert (vendt over\(x\)-aksen). Vi kan skrive dette som en stykkevis funksjon: \(\displaystyle f\left( x \right)= \ left \ {\begin{array}{l}{{x}^{2}}-4\,\,\,\,\,\,\,\,\,\tekst{if }x <-2\tekst{ eller }x >2 \ \ – {{x}^{2}} \ tekst{+ 4}\,\,\,\,\,\,\tekst{if }-2\le x \ le 2 \ end{array} \ høyre.\ ) Vi kan se at dette startet en transformert kvadratisk funksjon \(y={{x}^{2}}-4\) med en absolutt verdi rundt den, siden alle\ (y\) verdier er positive: \(y=\left / {{{x}^{2}}-4} \ right/\).		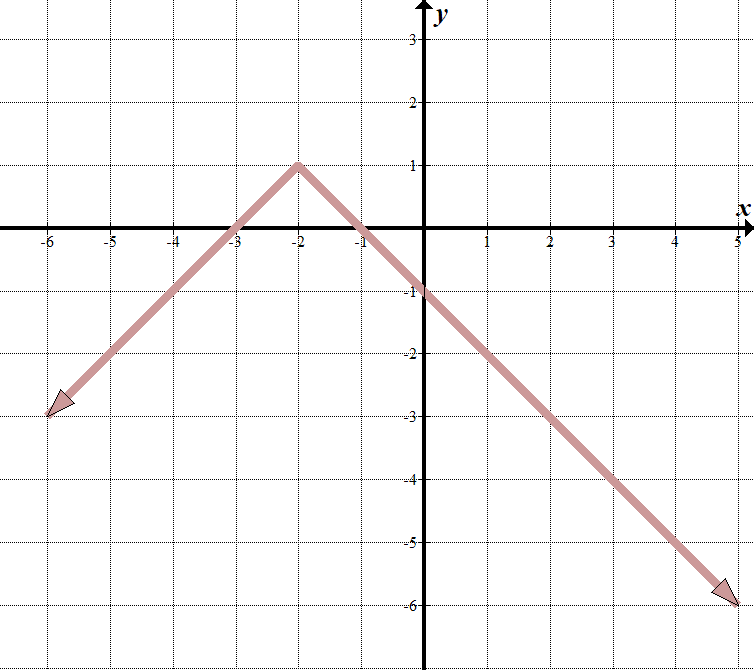vi ser at vår «grenselinje» er på \(x=-2\), så det som er inne i absoluttverditegnet må være \(x+2\). når \(x> -2\), kan vi se at likningen av linjen er \(y= – x-1\). Når \(x <-2\), er linjen \(y=x+3\). Vi kan skrive dette som en stykkevis funksjon: \(\displaystyle f\left( x \right)= \ left \ {\begin{array}{l} – x-1\,\,\,\,\,\,\tekst{if }x>-2\\x+3\,\,\,\,\,\,\,\,\,\,\tekst{if }x\le -2 \ end{array} \ høyre.\) det er sannsynligvis lettere å skrive dette som en transformert absoluttverdifunksjon. Vi kan se at overordnet absoluttverdifunksjon er vendt vertikalt, flytt til venstre 2 og opp 1. Vår absolutte verdi ligning er \(y= – \ venstre / {x + 2} \ høyre|\,\,+\,\,1\). Dette er det samme som stykkevis funksjon ovenfor. Prøv det – det fungerer!

Transformasjoner Av Stykkevis Funksjoner

la oss gjøre en transformasjon av en stykkevis funksjon. Vi lærte hvordan Om Foreldrefunksjoner og Deres Transformasjoner her i Foreldregrafer og Transformasjoner-delen. Du vil sannsynligvis lese denne delen først, før du prøver en stykkevis transformasjon.

la oss transformere følgende stykkevis funksjon vendt rundt\(x\)-aksen, vertikalt strukket med en faktor på 2 enheter, 1 enhet til høyre og 3 enheter opp.

vi vil tegne \(-2f\venstre( x-1 \høyre)+3\), hvor:

\(\displaystyle f\venstre( x \høyre)=\venstre\{ \begin{align}x+4\,\,\,\,\,\,\,\,&\tekst{ if }x<&\tekst{ hvis 1 }\le x<4 \ \ x-5\,\,\,\,\,\,\,\,& \tekst{ if }x\ge 4\end{align} \høyre.\ )

La oss sørge for at vi bruker» grense » – punktene når vi fyller ut t-diagrammet for transformasjonen. Husk at transformasjonene i parentesene er gjort til \(x\) (gjør motsatt matte), og utenfor er gjort til \(y\). For å komme opp med et t-diagram, som vist i tabellen nedenfor, kan vi bruke viktige punkter, inkludert to punkter på hver av «grenselinjene».Merk at fordi denne transformasjonen er komplisert, kan vi komme opp med en ny stykkevis funksjon ved å transformere de 3 » stykkene «og også transformere»\(x\) «s hvor grensepunktene er (legger til 1, eller går til høyre 1), siden vi gjør motsatt matte for»\(x\) » s. For å få de nye funksjonene i hvert intervall, kan vi bare erstatte «\(x-1\) » for «\(x\) » i den opprinnelige ligningen, multipliser med -2, og legg deretter til 3. For eksempel \(\displaystyle-2f \ venstre ({x-1} \ høyre) + 3=-2 \ venstre + 3=-2 \ venstre ({x + 3} \ høyre) + 3= – 2x-3\).

\(\displaystyle-2f \ venstre ({x-1} \ høyre) + 3 = \ venstre\ {\begin{array} {l}-2\venstre ({\venstre ({x-1} \høyre)+4} \ høyre)+3=-2x-3,\,\,\,\,\tekst{ if }x-1<1\,\,\,\venstre( {x<2} \ høyre)\\-2 \ venstre (2 \ høyre)+3=-1,\,\,\,\,\tekst{ if }\,\tekst{ 2 }\le x<5 \ \ -2 \ venstre ({\venstre ({x-1} \ høyre) -5} \ høyre) + 3= – 2x+15,\,\,\,\,\tekst{ if }x \ ge 5 \ end{array} \ høyre.\)

her er «før» og «etter» grafer, inkludert t-diagrammet:

Piecewise Parent Function	T-chart	Transformation of Function
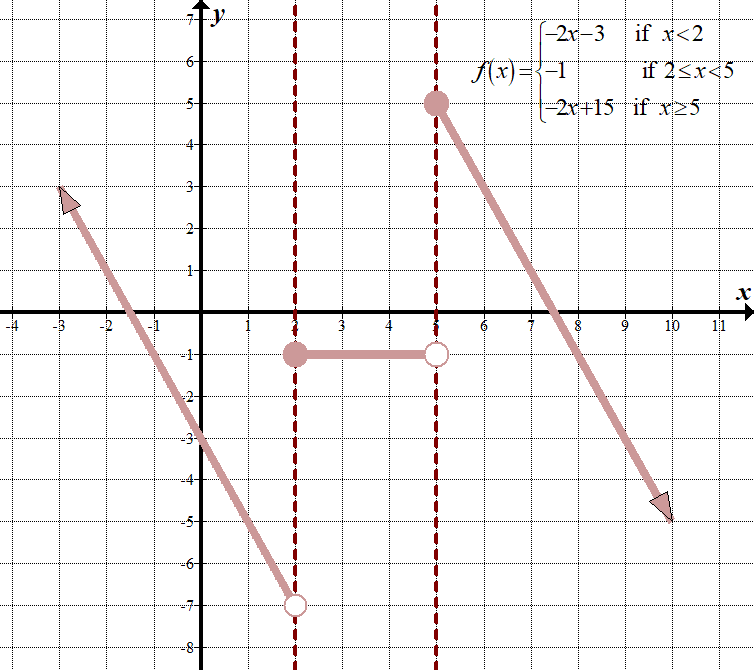
\(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}x+4\,\,\,\,\,\,\,\,\text{if }x<1\\2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{if 1 }\le x<4\\x-5\,\,\,\,\,\,\,\,\text{if }x\ge 4\end{array} \right.\)	x + 1 x y –2y+3 1 0 4 –5 2 1 5 –7 2 1 2 –1 5 4 2 –1 5 4 –1 5 8 7 2 –1	\(\displaystyle -2f\left( {x-1} \right)+3=\left\{ \begin{array}{l}-2x-3\,\,\,\,\,\,\,\,\,\text{if }x<2\\-1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{if 2}\le x<5\\-2x+15\,\,\,\,\,\,\text{if }x\ge 5\end{array} \right.\)

Piecewise Function Word Problems

Problem:

din favoritt hund groomer kostnader i henhold til hundens vekt. Hvis hunden din er 15 pund og under, belaster groomer $ 35. Hvis hunden din er mellom 15 og 40 pund, belaster hun $40. Hvis hunden din er over 40 pounds, belaster hun $40, pluss en ekstra $2 for hvert pund.

(A) Skriv en stykkevis funksjon som beskriver hva hunden din groomer kostnader.

(b) Graf funksjonen.

(c) Hva ville groomer lade hvis din søte hunden veier 60 pounds?

Løsning:

(a) vi ser at «grensepunktene» er 15 og 40, siden disse er vektene der prisene endres. Siden vi har to grensepunkter, har vi tre ligninger i vår stykkevis funksjon. Vi må starte på 0, siden hunder må veie over 0 pounds:

\(\displaystyle f\venstre( x \høyre)= \ venstre\ {\beginn{array}{l} \ tekst{ }……\,\,\,\,\,\,\,\,\,\tekst{if }0 < x \ le 15 \ \ \ tekst{ }……\,\,\,\,\,\,\,\,\,\tekst{if }15 < x \ le 40 \ \ \ tekst{ }……\,\,\,\,\,\,\,\,\,\tekst{if }x > 40 \ end{array} \ høyre.\)

vi leter etter «svarene» (hvor mye grooming koster) til «spørsmålene» (hvor mye hunden veier) for de tre prisene. De to første er bare flate avgifter (henholdsvis$35 og $40). Den siste ligningen er litt vanskeligere; groomer belaster $40 pluss $2 for hvert pund over 40. La oss prøve ekte tall: hvis hunden din veier 60 pounds, vil hun belaste $40 pluss $2 ganger \(20 (60-40)\). Vi gjør dette til en ligning: \(40 + 2 (x–40)\), som forenkler til \(2x-40\) (se hvordan 2 er skråningen?).

hele stykkevis funksjon er:

\(\displaystyle f\venstre( x \høyre)= \ venstre\ {\beginn{array}{l} \ tekst{ }35\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\tekst{if }0 < x \ le 15 \ \ \ tekst{ }40\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\tekst{if }15<x\le 40\\\tekst{ }40+2 \ venstre ({x-40} \ høyre)\,\,\,\,\,\,\tekst{if }x > 40 \ end{array} \ høyre.\) eller \(\displaystyle f\venstre (x \ høyre)= \ venstre\ {\beginn{array}{l} \ tekst{ }35\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\tekst{if }0 < x \ le 15 \ \ \ tekst{ }40\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\tekst{if }15 < x \ le 40 \ \ \ tekst{ }2x-40\,\,\,\,\,\,\,\tekst{if }x > 40 \ end{array} \ høyre.\)

(b) la oss graf:Merk at denne stykkevis ligningen ikke er kontinuerlig. Legg også merke til at et rimelig domene for dette problemet kan være \(\left ({0,200} \ right]\) (gitt hunder veier ikke over 200 pounds!) og et rimelig utvalg kan være \(\left \ cup \ left\).(c) hvis hunden din veier 60 pounds, kan vi enten bruke grafen eller funksjonen for å se at du må betale $80. Whoa! Det koster mer enn en menneskelig hårklipp (minst mine hårklipp)!

Problem:

du planlegger Å selge She Love Math T-skjorter som en fundraiser. Engros t-skjorte selskapet belaster deg $10 en skjorte for de første 75 skjorter. Etter de første 75 skjorter du kjøper opp til 150 skjorter, vil selskapet senke prisen til $ 7,50 per skjorte. Etter at du har kjøpt 150 skjorter, vil prisen reduseres til $5 per skjorte. Skriv en funksjon som modellerer denne situasjonen.

Løsning:

Vi ser at «grensepunktene» er 75 og 150, siden disse er antall t-skjorter kjøpt der prisene endres. Siden vi har to grensepunkter, har vi tre ligninger i vår stykkevis funksjon. Vi starter med \(x\ge 1\), siden vi antar at minst en skjorte er kjøpt. Merk i dette problemet, antall t-skjorter kjøpt (\(x\)), eller domenet, må være et heltall, men denne begrensningen bør ikke påvirke utfallet av problemet.

\(\displaystyle f\venstre( x \høyre)=\venstre\{ \begin{array}{l}\text {}….. \text{ if }1\le x\le 75\\text {}…..\text{ if }75<x\le 150\\\tekst {}……\tekst{ if }x>150\end{array}\høyre.\ )

vi leter etter «svar» (total kostnad på t-skjorter) til «spørsmål» (hvor mange er kjøpt) for de tre områder av priser.

for opp til og med 75 skjorter, er prisen $10, så den totale prisen ville \(10x\). For mer enn 75 skjorter, men opptil 100 skjorter, er kostnaden $ 7,50, men de første 75 t-skjortene vil fortsatt koste $10 per skjorte. Den andre funksjonen inkluderer $ 750 brukt på de første 75 skjortene (75 ganger $10), og inkluderer også $ 7,50 ganger antall skjorter over 75, som ville være \((x-75)\). For eksempel, hvis du kjøpte 80 skjorter, må du bruke \(\$10\ganger 75=\$750\), pluss \(\$7,50 \ ganger 5\,\) (80 – 75) for skjortene etter den 75. skjorten.

På samme måte, for over 150 skjorter, ville vi fortsatt betale $10 prisen opp gjennom 75 skjorter, $ 7.50 pris for 76 til 150 skjorter (75 flere skjorter), og deretter $5 per skjorte for antall skjorter kjøpt over 150. Vi betaler \(10(75)+7.50(75)+5(x-150)\) for\ (x\) skjorter. Sett inn tall og prøv det!

hele stykkevis funksjon er:

\(\displaystyle f\venstre( x \høyre)=\venstre\{ \begin{array}{l}\text{ }10x\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\tekst{if }1\le x \ le 75 \ \ \ tekst{ }7,5 x \ tekst { } + \ tekst{ }187.5\,\,\,\,\,\tekst{if 7}5 <x \ le 150 \ \ \ tekst{ }5x+562.5\,\,\,\,\,\,\,\,\,\,\tekst{ if }x >150 \ end{array} \ høyre.\) eller \(\displaystyle f\venstre (x \ høyre)= \ venstre \ {\begin{array}{l} \ text{ }10x\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\tekst{if }1\le x \ le 75 \ \ \ tekst{ }7,5 x \ tekst { } + \ tekst{ }187.5\,\,\,\,\,\tekst{if 7}5 <x \ le 150 \ \ \ tekst{ }5x+562.5\,\,\,\,\,\,\,\,\,\,\,\tekst{if }x >150 \ end{array} \ høyre.\ )

Problem:

en busstjeneste koster $50 for de første 400 miles, og hver ekstra 300 miles (eller en brøkdel av dette) legger til $10 til prisen.

Bruk en stykkevis funksjon for å representere bussprisen i forhold til avstanden i miles.Dette er faktisk et vanskelig problem, men la oss først tenke først om «grensepunktet», som er 400. Det er ganske greit når turen er mindre enn 400 miles; kostnaden er $50.For større enn 400 miles må vi trekke ut de første 400 miles (men husk å inkludere de første $ 50), dele antall miles igjen med 300 miles (og runde opp, hvis det er en brøkdel), og multipliser det med $10.

den vanskelige delen er når vi «runde opp» for en del av de neste 300 miles. Vi kan bruke en» tak » – funksjon (betegnet med \(\left \ lceil {}\right \ rceil\)); denne funksjonen gir minst heltall som er større enn eller lik inngangen; for eksempel er taket på både 3,5 og 4 4.

Dette er Hva vi har:

\(\displaystyle f\venstre( x \høyre)=\venstre\{ \begin{array}{l}\text{ }50 \ text{ }\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\tekst{if }0\le x \ le 400\\ \ tekst{ }50 + 10 \ ganger \venstre \ lceil {\frac{{x-400}}{{300}}} \høyre \ rceil \ tekst{ }\,\,\,\,\,\,\tekst{ if }x > 400 \ end{array} \ høyre.\ )

La oss prøve det! Hvis vi har en 1500 kilometer tur, vil kostnaden være \(\displaystyle 50+10 \ ganger \ venstre \ lceil {\frac{{1500-400}}{{300}}} \høyre\rceil \ text{ }=50 + 10 \ ganger 4 = \$90\).

Problem:

hvilken verdi av \(\boldsymbol{a}\) ville gjøre denne stykkevis funksjonen kontinuerlig?

\(\displaystyle f\venstre( x \høyre)=\venstre\{ \begin{array}{l}3{{x}^{2}}+4\,\,\,\,\,\tekst{ if }x <-2\\5x+\boldsymbol{a}\,\,\,\,\,\,\,\,\tekst{if }x\ge -2 \ end{array} \ høyre.\)

Løsning:

for at piecewise-funksjonen skal være kontinuerlig, ved grensepunktet (der funksjonen endres), må de to \(y\) verdiene være de samme. Vi kan plugge inn -2 for \(x\) i begge funksjonene og sørge for at \(y\) er de samme

\(\begin{align}3{{x}^{2}}+4&=5x + a \ \ 3 {{\left ({-2} \ right)}^{2}}+4&=5\venstre( {-2} \høyre)+a\\12+4&=-10+a\\a&=26\end{align}\)

Hvis \(a=26\), vil piecewise funksjonen er kontinuerlig!

Lær disse reglene, og praksis, praksis, praksis!

Mer Praksis: Bruk mathway-widgeten nedenfor for å prøve å skrive En Stykkevis Funksjon. Klikk På Send (den blå pilen til høyre for problemet) og klikk På Skriv Absoluttverdien Som Stykkevis for å se svaret.

du kan også skrive inn ditt eget problem, eller klikke på de tre prikkene i øvre høyre hjørne og klikk på «Eksempler» for å bore ned etter emne.

hvis du klikker På Trykk for å se trinnene, Eller Klikk Her, kan du registrere Deg Hos Mathway for en gratis prøveversjon, og deretter oppgradere til et betalt abonnement når som helst (for å få alle typer matematiske problemer løst!).

Videre Til Matriser og Løse Systemer Med Matriser-du er klar!