Koordinatplanet
Læringsmål(er)
· Plott bestilte par på et koordinatplan.
* Gitt et bestilt par, bestem kvadranten.
Innledning
koordinatplanet ble utviklet århundrer siden og raffinert av den franske matematikeren René Descartes. Til hans ære kalles systemet Noen ganger Det Kartesiske koordinatsystemet. Koordinatplanet kan brukes til å plotte punkter og graflinjer. Dette systemet tillater oss å beskrive algebraiske relasjoner i visuell forstand, og hjelper oss også med å lage og tolke algebraiske konsepter.
Bli Kjent Med Koordinatplanet
du har sannsynligvis brukt et koordinatplan før. Har du for eksempel noen gang brukt et gridded overlegg for å kartlegge posisjonen til et objekt? (Dette gjøres ofte med veikart også.)

dette «kartet» bruker et horisontalt og vertikalt rutenett for å formidle informasjon om et objekts plassering. Legg merke til at bokstavene A-F er oppfort langs toppen, og tallene 1-6 er oppfort langs venstre kant. Den generelle plasseringen av et element på dette kartet kan bli funnet ved å bruke bokstaven og nummeret på rutenettet. For eksempel kan du finne elementet som finnes på torget » 4F » ved å bevege fingeren langs vannrett til bokstaven F og deretter rett ned slik at du er i tråd med 4. Du finner en blå plate er på dette stedet på kartet.
koordinatplanet har lignende elementer som rutenettet vist ovenfor. Den består av en horisontal akse og en vertikal akse, talllinjer som krysser i rette vinkler. (De er vinkelrett på hverandre.)
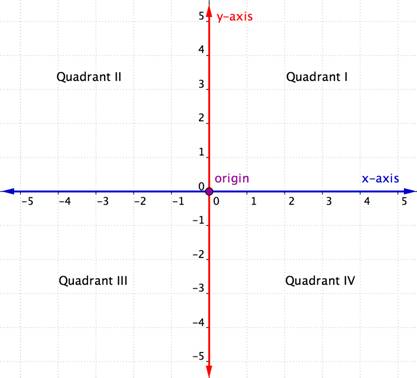
den horisontale aksen i koordinatplanet kalles x-aksen. Den vertikale aksen kalles y-aksen. Punktet som de to aksene krysser kalles opprinnelsen. Opprinnelsen er 0 på x-aksen og 0 på y-aksen.
de kryssende x-og y-aksene deler koordinatplanet i fire seksjoner. Disse fire delene kalles kvadranter. Kvadranter er navngitt Ved Hjelp Av Romertall I, II, III, OG IV begynner med øverste høyre kvadrant og flytte mot klokken.
Steder på koordinatplanet er beskrevet som bestilte par. Et bestilt par forteller deg plasseringen av et punkt ved å knytte punktets plassering langs x-aksen (den første verdien av det bestilte paret) og langs y-aksen (den andre verdien av det bestilte paret).
i et ordnet par, for eksempel (x, y), kalles den første verdien x-koordinaten og den andre verdien er y-koordinaten. Merk at x-koordinaten er oppført før y-koordinaten. Siden opprinnelsen har en x-koordinat på 0 og en y-koordinat på 0, er det bestilte paret skrevet (0, 0).
Vurder punktet nedenfor.
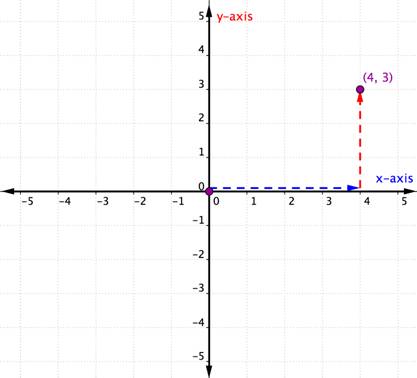
for å identifisere plasseringen av dette punktet, start ved opprinnelsen (0, 0) og flytt til høyre langs x-aksen til du er under punktet. Se på etiketten på x-aksen. 4 indikerer at du fra opprinnelsen har reist fire enheter til høyre langs x-aksen. Dette er x-koordinaten, det første nummeret i det bestilte paret.
fra 4 på x-aksen beveger du opp til punktet og merker nummeret som det justerer på y-aksen. 3 indikerer at du etter å ha forlatt x-aksen reiste 3 enheter opp i vertikal retning, retningen til y-aksen. Dette nummeret er y-koordinaten, det andre nummeret i det bestilte paret. Med en x-koordinat på 4 og en y-koordinat på 3, har du det bestilte paret (4, 3).
La oss se på et annet eksempel.
|
Example |
||
|
Problem |
Describe the point shown as an ordered pair. |
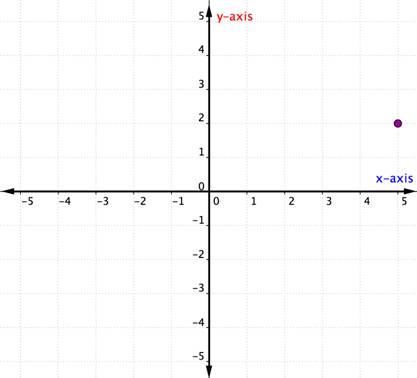 |
|
(5, y) |
begynn ved opprinnelsen og beveg deg langs x-aksen. Dette er x-koordinaten og er skrevet først i det bestilte paret. |
(5, 2) |
flytt fra 5 opp til det bestilte paret og les tallet på y-aksen. Dette er y-koordinaten og er skrevet andre i det bestilte paret. |
|
Svar |
punktet som vises som et bestilt par er (5, 2). |
|
Plottepunkter I Koordinatplanet
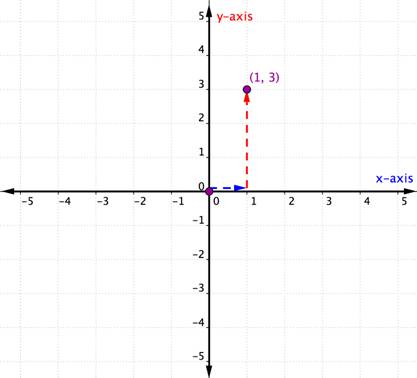
nå som du vet hvordan du bruker x – og y-aksene, kan du også plotte et bestilt par. Bare husk, begge prosessene starter ved opprinnelsen-begynnelsen! Eksemplet som følger viser hvordan du grafer det bestilte paret (1, 3).
|
Example |
||
|
Problem |
Plot the point (1, 3). |
|
|
|
||
|
The x-coordinate is 1 because it comes first in the ordered pair. Start ved opprinnelsen og flytt en avstand på 1 enhet i en positiv retning (til høyre) fra opprinnelsen langs x-aksen. |
y-koordinaten er 3 fordi den kommer andre i det bestilte paret. Herfra beveger du direkte 3 enheter i positiv retning (opp). Hvis du ser over til y-aksen, bør du være lined opp med 3 på den aksen. |
Svar |
Tegn et punkt på dette stedet og merk punktet (1, 3). |
i det forrige eksemplet var både x – og y-koordinatene positive. Når en (eller begge) av koordinatene til et bestilt par er negativt, må du bevege deg i negativ retning langs en eller begge akser. Tenk på eksemplet nedenfor der begge koordinatene er negative.
|
Example |
||
|
Problem |
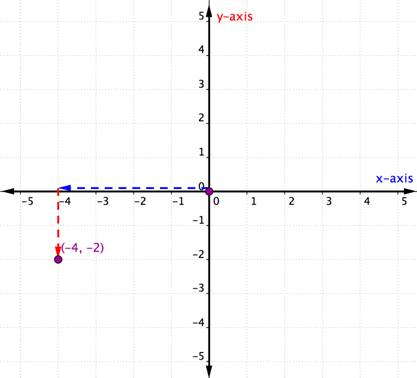
Plot the point (−4, −2). |
|
|
|
||
|
The x-coordinate is −4 because it comes first in the ordered pair. Start ved opprinnelsen og flytt 4 enheter i negativ retning (venstre) langs x-aksen. |
y-koordinaten er -2 fordi den kommer andre i det bestilte paret. Flytt nå 2 enheter i negativ retning (ned). Hvis du ser over til y-aksen, bør du være lined opp med -2 på den aksen. |
Svar |
Tegn et punkt på dette stedet og merk punktet (-4, -2). |
trinnene for å plotte et punkt er oppsummert nedenfor.
Trinn For Å Plotte Et Bestilt Par (x, y) i Koordinatplanet
O Bestem x-koordinaten. Begynn ved opprinnelsen, flytt horisontalt, retningen til x-aksen, avstanden gitt av x-koordinaten. Hvis x-koordinaten er positiv, flytt til høyre; hvis x-koordinaten er negativ, flytt til venstre.
O Bestemme y-koordinaten. Begynn ved x-koordinaten, flytt vertikalt, retningen til y-aksen, avstanden gitt av y-koordinaten. Hvis y-koordinaten er positiv, flytt opp; hvis y-koordinaten er negativ, flytt ned.
O Tegn et punkt på sluttstedet. Merk punktet med det bestilte paret.
Hvilket punkt representerer det bestilte paret (-2, -3)?
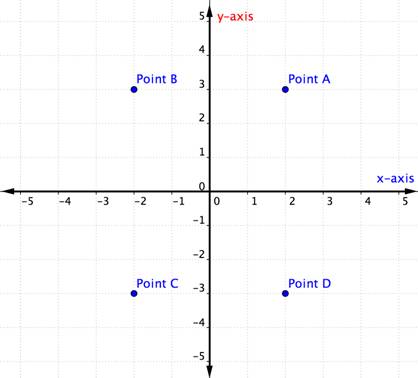
De Fire Kvadrantene
Bestilte par innenfor en bestemt kvadrant deler visse egenskaper. Se på hver kvadrant i grafen nedenfor. Hva merker du om tegnene på x-og y-koordinatene til punktene i hver kvadrant?
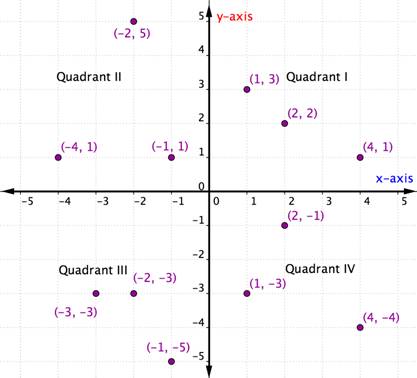
innenfor hver kvadrant er tegnene på x-koordinatene og y-koordinatene til hvert bestilt par de samme. De følger også et mønster, som er skissert i tabellen nedenfor.
Når du vet om kvadrantene i koordinatplanet, kan du bestemme kvadranten til et bestilt par uten å tegne det ved å se på diagrammet ovenfor. Her er en annen måte å tenke på det.
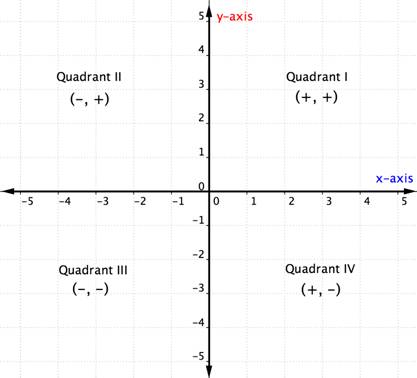
eksemplet nedenfor beskriver hvordan du bestemmer kvadrantplasseringen av et punkt bare ved å tenke på tegnene på koordinatene. Å tenke på kvadrantplasseringen før du plotter et punkt, kan hjelpe deg med å forhindre en feil. Det er også nyttig kunnskap for å sjekke at du har plottet et punkt riktig.
Hva skjer hvis et bestilt par har en x-eller y-koordinat på null? Eksemplet nedenfor viser grafen for det bestilte paret (0, 4).
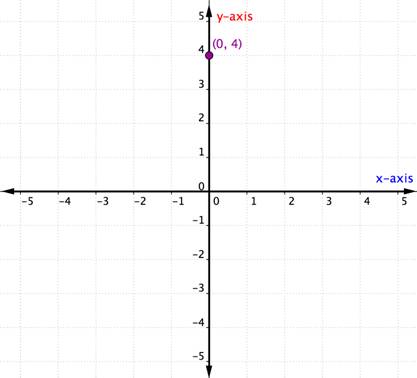
et punkt plassert på en av aksene anses ikke å være i en kvadrant. Det er bare på en av aksene. Når x-koordinaten er 0, er punktet plassert på y-aksen. På samme måte vil ethvert punkt som har en y-koordinat på 0 være plassert på x-aksen.
Hvilken av beskrivelsene nedenfor beskriver best plasseringen av punktet (8, 0)?
A) Kvadrant i
B) det er på x-aksen
C) det er på y-aksen
D) koordinatplanet
Sammendrag
Koordinatplanet Er et system For å tegne grafer og beskrive punkter og linjer. Koordinatplanet består av en horisontal (x-) akse og en vertikal (y-) akse. Krysset mellom disse linjene skaper opprinnelsen, som er punktet (0, 0). Koordinatplanet er delt inn i fire kvadranter. Sammen tillater disse funksjonene i koordinatsystemet grafisk representasjon og kommunikasjon om punkter, linjer og andre algebraiske konsepter.