Konigsberg er en by på Preger-Elven, som i det 18. århundrevar en tysk by, men nå er russisk. Innenfor byen er toriverøyer som er forbundet med bankene med syv broer (som vist nedenfor).

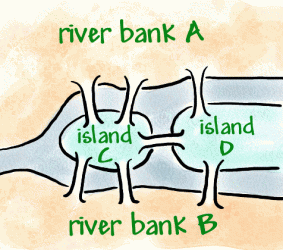
det ble en tradisjon å prøve å gå rundt i byen på en måte som bare krysset hver bro en gang, men det viste seg å være en difficultproblem. Leonhard Euler, En Sveitsisk matematiker i tjeneste forden russiske keiserinne Catherine The Great, hørte om problemet.I 1736 beviste Euler at turen ikke var mulig å gjøre. Hanbevist dette ved å oppfatte et slags diagram kalt et nettverk, detbestår av hjørner(prikker hvor linjer møtes) og buer (linjer).

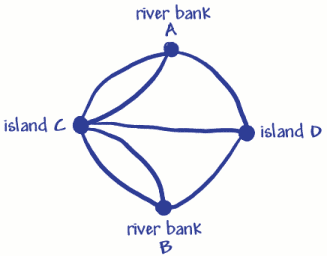
han brukte fire prikker (hjørner) for de to elvebreddene og toøyene. Disse har blitt merket A, B Og C, D. de syv linjene (buer) er de syv broene. Du kan se at 3 broer (buer)bli med til elvebredden A, og 3 bli med til elvebredden B. 5 broer (buer)bli med til øya C, og 3 bli med til øya D. Dette betyr at allenvertices har et merkelig antall buer, så de kalles oddvertices. (Et jevnt toppunkt må ha et jevnt antall buerbli med på det).
Husk at problemet var å reise rundt i byen krysset eachbridge bare en gang. På eulers nettverk betydde dette å spore over hverark bare en gang, besøke alle hjørnene. Euler beviste at det ikke kunne gjøres fordi han jobbet ut det for å ha et merkelig toppunkt du ville ha til å begynne eller avslutte turen på det toppunktet. (Tenk på det).Siden det bare kan være en begynnelse og en ende, kan det bare være to odde hjørner hvis du bare skal kunne spore over eacharc en gang. Siden broproblemet har 4 odde hjørner, er det bare ikke mulig å gjøre! Hva skjer hvis det ikke er noen merkelige hjørner påalt? Kan dette nettverket spores?

oppfinnelsen av nettverk begynte en helt ny type geometri kalttopologi. Topologi brukes nå på mange måter, inkludert for planleggingog kartlegging av jernbanenett. (Ahhh! Togene måtte komme inndet….)