- Læringsmål
- Arbeid Mot Tyngdekraften
- Konvertering Mellom Potensiell Energi og Kinetisk Energi
- Bruke Potensiell Energi For Å Forenkle Beregninger
- Eksempel 1. Kraften Til Å Slutte Å Falle
- Strategi
- Løsning
- Diskusjon
- Eksempel 2. Finne Hastigheten På En Berg-Og Dalbane fra Sin Høyde
- Strategi
- Løsning For Del 1
- løsning for del 2
- Diskusjon og Implikasjoner
- Making Connections: Take-Home Investigation-Konvertere Potensial Til Kinetisk Energi
- Seksjonssammendrag
- Konseptuelle Spørsmål
- Problemer& Øvelser
- Ordliste
- Utvalgte Løsninger på Problemer& Øvelser
Læringsmål
ved slutten av denne delen vil du kunne:
- Forklare gravitasjonspotensiell energi i form av arbeid utført mot tyngdekraften.
- Viser at gravitasjonspotensialenergien til et objekt med masse m i høyden h på Jorden er gitt Av PEg = mgh.
- Viser hvordan kunnskap om potensiell energi som posisjonsfunksjon kan brukes til å forenkle beregninger og forklare fysiske fenomener.
Arbeid Mot Tyngdekraften
Klatring av trapper og løfteobjekter er arbeid i både vitenskapelig og daglig forstand—det er arbeid mot gravitasjonskraften. Når det er arbeid, er det en transformasjon av energi. Arbeidet mot gravitasjonskraften går inn i en viktig form for lagret energi som vi vil utforske i denne delen.

Figur 1. (a) arbeidet som gjøres for å løfte vekten, lagres i massejordsystemet som gravitasjonspotensiell energi. (b) når vekten beveger seg nedover, overføres denne gravitasjonspotensielle energien til gjøkuret.
la oss beregne arbeidet med å løfte et objekt med masse m gjennom en høyde h, som I Figur 1. Hvis objektet løftes rett opp med konstant hastighet, er kraften som trengs for å løfte den, lik vekten mg. Arbeidet på massen er Da W = Fd = mgh. Vi definerer dette for å være gravitasjonspotensialenergien (PEg) satt inn i (eller oppnådd av) objektjordsystemet. Denne energien er knyttet til separasjonsstaten mellom to gjenstander som tiltrekker hverandre av gravitasjonskraften. For enkelhets skyld refererer vi til Dette Som Pinnen oppnådd av objektet, og anerkjenner at dette er energi lagret I jordens gravitasjonsfelt. Hvorfor bruker vi ordet «system»? Potensiell energi er en egenskap av et system i stedet for et enkelt objekt – på grunn av sin fysiske posisjon. Et objekts gravitasjonspotensial skyldes posisjonen i forhold til omgivelsene i Jordobjektsystemet. Kraften som påføres objektet er en ekstern kraft, fra utsiden av systemet. Når det gjør positivt arbeid, øker det gravitasjonspotensialenergien til systemet. Fordi gravitasjonspotensiell energi avhenger av relativ posisjon, trenger vi et referansenivå for å sette potensiell energi lik 0. Vi velger vanligvis dette punktet For Å Være Jordens overflate, men dette punktet er vilkårlig; det som er viktig er forskjellen i gravitasjonspotensiell energi, fordi denne forskjellen er hva som er relatert til arbeidet. Forskjellen i gravitasjonspotensiell energi av et objekt (I Jord-objekt-systemet) mellom to trinn av en stige vil være den samme for de to første trinnene som for de to siste trinnene.
Konvertering Mellom Potensiell Energi og Kinetisk Energi
Gravitasjonspotensiell energi kan omdannes til andre former for energi, for eksempel kinetisk energi. Hvis vi frigjør massen, vil gravitasjonskraften gjøre en mengde arbeid som er lik mgh på den, og dermed øke sin kinetiske energi med samme mengde (ved arbeidsenergiteoremet). Vi vil finne det mer nyttig å vurdere bare konverteringen Av PEg TIL KE uten eksplisitt å vurdere mellomtrinnet i arbeidet. (Se Eksempel 2.) Denne snarveien gjør det lettere å løse problemer ved hjelp av energi (hvis mulig) i stedet for eksplisitt å bruke krefter.
nærmere bestemt definerer vi endringen i gravitasjonspotensial energi ΔPEg til Å Være Δ = mgh, der vi for enkelhets skyld betegner endringen i høyde med h i stedet for den vanlige Δ. Merk at h er positiv når slutthøyden er større enn starthøyden, og omvendt. For eksempel, hvis en 0,500 kg masse hang fra en gjøkur er hevet 1.00 m, så er endringen i gravitasjonspotensiell energi
\begin{array}{lll}mgh&&(0,500\text{ kg})(9,80\text{ m/s}^2)(1.00\text{ m})\\\text{ }&&4.90\text{ kg}\cdot\text{m}^2\text{/s}^2=4.90\text{ j}\end{array}\\
merk at enhetene av gravitasjonspotensiell energi viser seg å være joules, det samme som for arbeid og andre former for energi. Når klokken går, senkes massen. Vi kan tenke på massen som gradvis gir opp sin 4.90 J av gravitasjonspotensiell energi, uten direkte å vurdere tyngdekraften som gjør arbeidet.
Bruke Potensiell Energi For Å Forenkle Beregninger

Figur 2. Endringen i gravitasjonspotensiell energi (ΔPEg) mellom punktene A og B er uavhengig av banen.
Ligningen Δ = mgh gjelder for enhver sti som har en endring i høyden på h, ikke bare når massen løftes rett opp. (Se Figur 2.) Det er mye lettere å beregne mgh (en enkel multiplikasjon) enn det er å beregne arbeidet gjort langs en komplisert bane. Ideen om gravitasjonspotensiell energi har den dobbelte fordelen at den er svært bredt anvendelig, og det gjør beregninger enklere.Fra nå av vil vi vurdere at enhver endring i vertikal stilling h av en masse m er ledsaget av en endring i gravitasjonspotensiell energi mgh, og vi vil unngå den tilsvarende, men vanskeligere oppgaven med å beregne arbeid utført av eller mot gravitasjonskraften.
Δ = mgh for enhver sti mellom de to punktene. Gravity er en av en liten klasse av krefter hvor arbeidet som utføres av eller mot kraften, bare avhenger av start-og sluttpunktene, ikke på banen mellom dem.
Eksempel 1. Kraften Til Å Slutte Å Falle
a 60.0-kg person hopper på gulvet fra en høyde på 3,00 m. hvis han lander stivt (med kneleddene komprimert med 0,500 cm), beregne kraften på kneleddene.
Strategi
denne personens energi blir brakt til null i denne situasjonen av arbeidet på ham ved gulvet når han stopper. Den første Pinnen blir forvandlet til KE når han faller. Arbeidet ved gulvet reduserer denne kinetiske energien til null.
Løsning
arbeidet som gjøres på personen ved gulvet når han stopper, er gitt Av W = Fd cos θ = – Fd, med et minustegn fordi forskyvningen mens du stopper og kraften fra gulvet er i motsatt retning (cos θ = cos 180º = -1). Gulvet fjerner energi fra systemet, så det gjør negativt arbeid.
den kinetiske energien personen har når han når gulvet, er mengden potensiell energi som går tapt ved å falle gjennom høyden h: KE = – Δ = – mgh.
avstanden d som personens knær bøyer er mye mindre enn høyden h på høsten, slik at den ekstra endringen i gravitasjonspotensiell energi under knærbøyningen ignoreres.
arbeidet W gjort ved gulvet på personen stopper personen og bringer personens kinetiske energi til null: W = – KE = mgh.
Kombinere denne ligningen med uttrykket For W gir-Fd = mgh.
Husker at h er negativ fordi personen falt ned, er kraften på kneleddene gitt av
\displaystyle{F}=-\frac{mgh}{d}=-\frac{\left(60.0\text{ kg}\høyre)\venstre(9.80\text{ m/s}^2\høyre)\venstre(-3.00\text{ m}\høyre)}{5.00\times10^{-3}\text{ m}}=3.53\times10^5\text{ N}\\
Diskusjon
En så stor kraft (500 ganger mer enn personens vekt) over den korte slagtiden er nok til å brekk bein. En mye bedre måte å pute sjokket på er å bøye bena eller rulle på bakken, og øke tiden over hvilken kraften virker. En bøyebevegelse på 0,5 m på denne måten gir en kraft 100 ganger mindre enn i eksemplet. En kengurus hopping viser denne metoden i aksjon. Kenguruen er det eneste store dyret som bruker hopping for bevegelse, men sjokket i hopping er polstret av bøyning av bakbenene i hvert hopp. (Se Figur 3.)

Figur 3. Arbeidet som gjøres av bakken på kenguruen reduserer sin kinetiske energi til null når den lander. Men ved å bruke kraften på bakken på bakbenene over en lengre avstand, blir virkningen på beinene redusert. (kreditt: Chris Samuel, Flickr)
Eksempel 2. Finne Hastigheten På En Berg-Og Dalbane fra Sin Høyde
- Hva er den endelige hastigheten på berg-og dalbanen vist i Figur 4 hvis den starter fra hvile på toppen av 20,0 m bakken og arbeid utført av friksjonskrefter er ubetydelig?
- Hva er dens endelige hastighet (igjen forutsatt ubetydelig friksjon) hvis starthastigheten er 5,00 m/s?
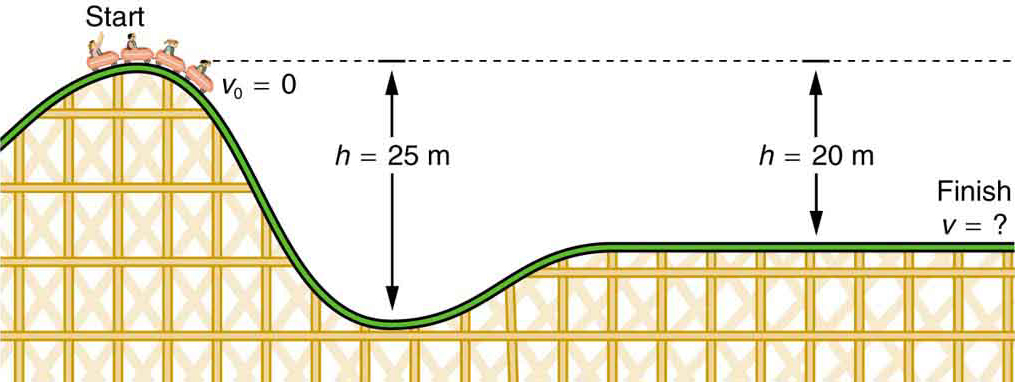
Figur 4. Hastigheten på en berg og dalbane øker som tyngdekraften trekker det nedoverbakke og er størst på sitt laveste punkt. Sett i form av energi, blir berg-og dalbane-jordens gravitasjonspotensial energi omdannet til kinetisk energi. Hvis arbeid utført ved friksjon er ubetydelig, konverteres alle Δ til KE.
Strategi
bergbanen mister potensiell energi når den går nedoverbakke. Vi forsømmer friksjon, slik at den gjenværende kraften som utøves av sporet, er den normale kraften, som er vinkelrett på bevegelsesretningen og ikke virker. Nettarbeidet på berg-og dalbanen gjøres da av tyngdekraften alene. Tapet av gravitasjonspotensiell energi fra å bevege seg nedover gjennom en avstand h er lik gevinsten i kinetisk energi. Dette kan skrives i ligningsform som-Δ = Δ. Ved hjelp av ligningene For PEg og KE kan vi løse for slutthastigheten v, som er ønsket mengde.
Løsning For Del 1
her er den første kinetiske energien null, slik at \ Delta \ text{KE}=\frac{1}{2}mv^2\\. Ligningen for endring i potensiell energi sier at Δ = mgh. Siden h er negativ i dette tilfellet, vil vi omskrive dette som Δ = – mg / h / for å vise minustegnet tydelig. Dermed blir-Δ = Δ til mg|h / =\frac{1}{2}{mv}^2\\.
Løse for v, finner vi at masse kansellerer og at v=\sqrt{2g / h/}\\.
Erstatte kjente verdier,
\begin{array}{lll}v&&\sqrt{2\venstre(9,80\tekst{ m/s}^2\høyre)\venstre(20,0\text{ m}\right)}\\\text{ }&&19.8\text{ m/s}\end{array}\\
løsning for del 2
igjen −δ = δ. I dette tilfellet er det innledende kinetisk energi, så
\ Delta \ text{KE}=\frac{1}{2}mv^2-\frac{1}{2}mv_0^2\\.
dermed mg|h / =\frac{1}{2}mv^2 – \frac{1}{2}mv_0^2\\.
Omorganisering gir \frac{1}{2}mv^2=mg|h|+\frac{1}{2}mv+0^2\\.dette betyr at den endelige kinetiske energien er summen av den opprinnelige kinetiske energien og gravitasjonspotensialenergien. Masse avbryter igjen, og v=\sqrt{2g / h/ + v_0^2}\\.
denne ligningen er veldig lik kinematikkligningen v=\sqrt{v_0^2 + 2ad}\\, men det er mer generelt—kinematikkligningen er gyldig bare for konstant akselerasjon, mens vår ligning ovenfor er gyldig for enhver bane uansett om objektet beveger seg med konstant akselerasjon. Nå erstatter kjente verdier
\begin{array}{lll}v&&\sqrt{2\venstre(9.80\tekst{ m/s}^2\høyre)\venstre(20.0\tekst{ m}\høyre)+\venstre(5.00\tekst{ m/s}\høyre)^2}\\\tekst{ }&&20.4 \ text{ m / s} \ end{array}\\
Diskusjon og Implikasjoner
merk først at masse kansellerer. Dette er helt i tråd med observasjoner gjort I Fallende Gjenstander at alle objekter faller i samme takt hvis friksjonen er ubetydelig. For det andre vurderes bare hastigheten på bergbanen; det er ingen informasjon om retningen når som helst. Dette avslører en annen generell sannhet. Når friksjonen er ubetydelig, avhenger hastigheten på en fallende kropp bare av starthastigheten og høyden, og ikke på massen eller banen som er tatt. For eksempel vil bergbanen ha samme slutthastighet om den faller 20,0 m rett ned eller tar en mer komplisert bane som den i figuren. Tredje, og kanskje uventet, er slutthastigheten i del 2 større enn i del 1, men langt mindre enn 5,00 m/s. Til slutt merk at hastigheten kan bli funnet i hvilken som helst høyde underveis ved å bare bruke riktig verdi av h på interessepunktet.vi har sett at arbeid utført av eller mot gravitasjonskraften bare avhenger av start-og sluttpunktene, og ikke på banen mellom, slik at vi kan definere det forenklende begrepet gravitasjonspotensiell energi. Vi kan gjøre det samme for noen andre krefter, og vi vil se at dette fører til en formell definisjon av loven om bevaring av energi.
Making Connections: Take-Home Investigation-Konvertere Potensial Til Kinetisk Energi
man kan studere konvertering av gravitasjonspotensiell energi til kinetisk energi i dette eksperimentet. På en jevn, jevn overflate, bruk en linjal av den typen som har et spor som løper langs lengden og en bok for å lage en skråning(Se Figur 5). Plasser en marmor på 10 cm-posisjonen på linjalen og la den rulle ned linjalen. Når den treffer overflaten, måler du tiden det tar å rulle en meter. Legg nå marmor på 20 cm og 30 cm posisjonene og mål igjen tiden det tar å rulle 1 m på jevn overflate. Finn hastigheten på marmor på flat overflate for alle tre posisjoner. Plot hastighet kvadrert versus avstanden reist av marmor. Hva er formen på hver tomt? Hvis formen er en rett linje, viser plottet at marmorens kinetiske energi i bunnen er proporsjonal med dens potensielle energi ved frigjøringspunktet.

Figur 5. En marmor ruller ned en linjal, og hastigheten på overflaten måles.
Seksjonssammendrag
- Arbeid utført mot tyngdekraften ved å løfte et objekt blir potensiell energi i objekt-Jord-systemet.
- endringen i gravitasjonspotensiell energi, Δ, er Δ = mgh, med h som økningen i høyde og g akselerasjonen på grunn av tyngdekraften.
- gravitasjonspotensialenergien til et objekt nær Jordens overflate skyldes dens posisjon i masse-Jord-systemet. Bare forskjeller i gravitasjonspotensiell energi, Δ, har fysisk betydning.
- når et objekt går ned uten friksjon, endres dens gravitasjonspotensielle energi til kinetisk energi som svarer til økende hastighet, slik AT Δ = −Δ
Konseptuelle Spørsmål
- I Eksempel 2 beregnet vi slutthastigheten til en berg-og dalbane som gikk ned 20 m i høyden og hadde en innledende hastighet på 5 m / s nedoverbakke. Anta at bergbanen hadde hatt en innledende hastighet på 5 m / s oppoverbakke i stedet, og den coasted oppoverbakke, stoppet og deretter rullet tilbake til et siste punkt 20 m under starten. Vi ville finne i så fall at den hadde samme siste hastighet. Forklar når det gjelder bevaring av energi.
- er arbeidet du gjør på en bok når du løfter den på en hylle, avhengig av banen som er tatt? På den tiden det tar? På høyden på hyllen? På massen av boken?
Problemer& Øvelser
- et vannkraftanlegg (Se Figur 6) konverterer gravitasjonspotensialenergien til vann bak en dam til elektrisk energi. (A) hva er gravitasjonspotensialenergien i forhold til generatorene til en innsjø med volum 50.0 km3 (masse = 5.00 × 1013 kg), gitt at innsjøen har en gjennomsnittlig høyde på 40,0 m over generatorene? (B) Sammenlign dette med energien som er lagret i en 9-megatonn fusjonsbombe.

Figur 6. Vannkraftanlegg(kreditt: Denis Belevich, Wikimedia Commons)
- (A) hvor mye gravitasjonspotensiell energi (i forhold til bakken som Den er bygget på) er lagret I Cheops Store Pyramide, gitt at massen er ca 7 × 109 kg og massesenteret er 36.5 m over det omkringliggende bakken? (b) hvordan sammenligner denne energien med det daglige matinntaket til en person?
- Anta at en 350-g kookaburra (en stor kingfisher fugl) plukker opp en 75-g slange og hever den 2,5 m fra bakken til en gren. (A) Hvor mye arbeid gjorde fuglen på slangen? (b) Hvor mye arbeid gjorde den for å heve sitt eget massesenter til grenen?
- I Eksempel 2 fant Vi at hastigheten på en berg-og dalbane som hadde gått ned 20,0 m var bare litt større når den hadde en starthastighet på 5,00 m / s enn når den startet fra hvile. Dette innebærer at Δ >> KEi. Bekreft denne erklæringen ved å ta forholdet MELLOM Δ og KEi. (Merk at masse kansellerer.)
- en 100 g lekebil drives av en komprimert fjær som begynner å bevege seg. Bilen folger det buede sporet I Figur 7. Vis at slutthastigheten til leketøybilen er 0,687 m / s hvis starthastigheten er 2,00 m / s og den kyster opp den friksjonsløse skråningen, og får 0,180 m i høyde.

Figur 7. En lekebil beveger seg opp et skrå spor. (kreditt: Leszek Leszczynski, Flickr)
- i en downhill ski rase, overraskende, liten fordel er oppnådd ved å få en løpende start. (Dette skyldes at den første kinetiske energien er liten sammenlignet med gevinsten i gravitasjonspotensiell energi på selv små åser.) For å demonstrere dette, finn den endelige hastigheten og tiden det tar for en skiløper som skier 70,0 m langs en 30º skråning som forsømmer friksjon: (a) Starter fra hvile. (b) Starter med en innledende hastighet på 2,50 m/s. (c) overrasker svaret deg? Diskuter hvorfor det fortsatt er fordelaktig å få en løpende start i svært konkurransedyktige hendelser.
Ordliste
gravitasjonspotensiell energi: energien et objekt har på grunn av sin posisjon i et gravitasjonsfelt
Utvalgte Løsninger på Problemer& Øvelser
1. (a) 1.96 × 1016 J; (b) forholdet mellom gravitasjonspotensiell energi i sjøen til energien lagret i bomben er 0.52. Det vil si at energien som er lagret i sjøen, er omtrent halvparten i en 9-megatonfusjonsbombe.
3. (a) 1,8 J; (b) 8,6 j
5. {v}_{f}=\sqrt{2gh + {v_0}^2}=\sqrt{2 \ venstre(9.80 \ tekst{ m / s}^2\høyre) \ venstre(-0.180 \ tekst{ m} \ høyre) + \ venstre (2.00\tekst{ m/s}\høyre)^2} = 0.687 \ tekst{ m / s}\\