noen interessante ting om vinkler og sirkler.
- Innskrevet Vinkel
- Innskrevne Vinkelteoremer
- Eksempel: hva er Størrelsen På Vinkel POQ? (O er sirkelens senter)
- Eksempel: hva er Størrelsen På Vinkel CBX?
- Vinkel i En Halvcirkel (Thales’ Teorem)
- En Annen god grunn til at det fungerer
- Eksempel: Hva er Størrelsen På Vinkel BAC?
- Finne En Sirkelsenter
- Syklisk Firkant
- eksempel: hva er størrelsen på vinkel wxy?
Innskrevet Vinkel
Først av, en definisjon:
Innskrevet Vinkel: en vinkel laget av punkter som sitter på sirkelens omkrets.
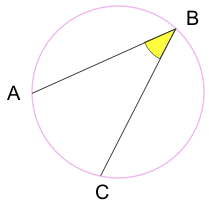
A Og c er «endepunkter»
B Er » apex-punktet «
Spill med det her:
når du flytter punkt» B», hva skjer med vinkelen?
Innskrevne Vinkelteoremer
en innskrevet vinkel a° er halvparten av den sentrale vinkelen 2a°
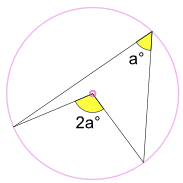
(Kalt Vinkelen Ved Senterteoremet)
Og (holder endepunktene faste) …
… vinkelen a° er alltid den samme,
uansett hvor den er på samme bue mellom endepunkter:
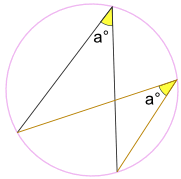
Vinkel a° er den samme.
(Kalt Vinklene Subtended Av Samme Arc Theorem)
Eksempel: hva er Størrelsen På Vinkel POQ? (O er sirkelens senter)
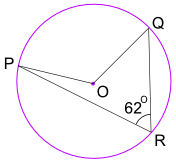
Vinkel POQ = 2 × Vinkel PRQ = 2 × 62° = 124°
Eksempel: hva er Størrelsen På Vinkel CBX?
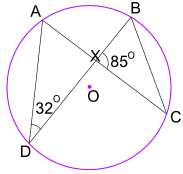
Vinkel ADB = 32° tilsvarer Også Vinkel ACB.
Og Vinkel ACB er også Lik Vinkel XCB.
Så i trekant bxc kjenner Vi Vinkel bxc = 85° og Vinkel XCB = 32°
bruk nå vinkler i en trekant legg til 180° :
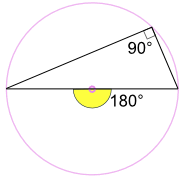
Vinkel i En Halvcirkel (Thales’ Teorem)
en vinkel innskrevet over en sirkels diameter er alltid en rett vinkel:
(endepunktene er hver ende av en sirkels diameter,
toppunktet kan være hvor som helst på sirkelen.omkrets.)
|
Hvorfor? Fordi: den innskrevne vinkelen 90° er halvparten av den sentrale vinkelen 180° (Ved Hjelp Av «Vinkel ved Senterets Teorem» ovenfor) |
En Annen god grunn til at det fungerer
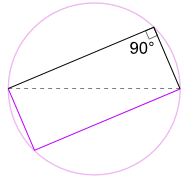
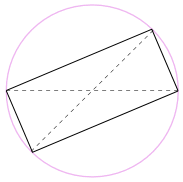
vi kan også rotere formen rundt 180° for Å lage Et Rektangel!
det er et rektangel, fordi alle sider er parallelle, og begge diagonaler er like.
og så er de indre vinklene alle rette vinkler (90°).
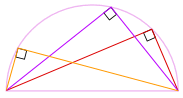
så der går vi! Uansett hvor den vinkelen er
på omkretsen, er det alltid 90°
Eksempel: Hva er Størrelsen På Vinkel BAC?
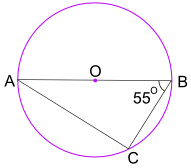
Vinkelen i Halvcirkelteoremet forteller oss At Vinkelen ACB = 90°
bruk nå vinkler av en trekant legg til 180° for å finne Vinkel BAC:
Finne En Sirkelsenter
vi kan bruke denne ideen til å finne en sirkelsenter:
- tegn en rett vinkel fra hvor som helst på sirkelens omkrets, deretter tegn diameteren der de To beina Treffer SIRKELEN
- gjør det igjen, men for en annen diameter
hvor diametrene krysser er sentrum!
Syklisk Firkant
|
A «Syklisk» Firkant har hvert toppunkt på en sirkels omkrets: |
|
en syklisk firkantet Motsatte Vinkler Legger Til 180°:
|
eksempel: hva er størrelsen på vinkel wxy?
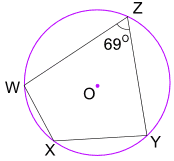
Opposite angles of a cyclic quadrilateral add to 180°