etter å ha forstått eksponentiell funksjon, er vårt neste mål den naturlige logaritmen.Gitt hvordan den naturlige loggen er beskrevet i mattebøker, er det lite «naturlig» om det: det er definert som den inverse av $e^x$, en merkelig nok eksponent allerede.

Men det er en frisk, intuitiv forklaring: den naturlige loggen gir deg tiden som trengs for å nå et visst nivå av vekst.

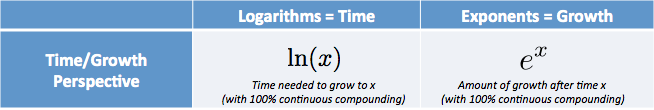
Anta at du har en investering i gummy bears (hvem gjør det ikke?) med en rente på 100% per år, vokser kontinuerlig. Hvis du vil ha 10x vekst, forutsatt kontinuerlig sammensetning, vil du vente bare $\ln(10)$ eller 2.302 år. Ser du ikke hvorfor det bare tar noen år å få 10x vekst? Ser du ikke hvorfor mønsteret ikke er 1, 2, 4, 8? Les mer om e.

e og Den Naturlige Loggen er tvillinger:

• $e^x$ er beløpet vi har etter å ha startet på 1.0 og vokser kontinuerlig for $x$ tidsenheter
• $\ln(X)$ (Naturlig Logaritme) er tiden for å nå beløp $x$, forutsatt at vi vokste kontinuerlig fra 1.0

Ikke så ille, ikke sant? Mens matematikerne scramble for å gi deg den lange, tekniske forklaringen, la oss dykke inn i den intuitive.

E Handler om Vekst

tallet e handler om kontinuerlig vekst. Som vi så sist, lar $e^x$ oss fusjonere og tid: 3 år ved 100% vekst er den samme som 1 år ved 300% vekst, når den kontinuerlig forsterkes.

Vi kan ta en kombinasjon av hastighet og tid (50% i 4 år) og konvertere prisen til 100% for enkelhets skyld (gir oss 100% i 2 år). Ved å konvertere til en hastighet på 100% må vi bare tenke på tidskomponenten:

Intuitivt betyr $e^x$:

• hvor mye vekst får jeg etter etter x tidsenheter (og 100% kontinuerlig vekst)
• for eksempel: etter 3 tidsperioder har jeg $e^3$ = 20,08 ganger mengden «ting».

$ e^x$ er en skaleringsfaktor som viser oss hvor mye vekst vi vil få etter $x$ tidsenheter.

Naturlig Logg Er Om Tid

den naturlige loggen er den inverse av $e^x$, en fancy term for motsatt. Når det gjelder fancy, er det latinske navnet logaritmus naturali, som gir forkortelsen ln.

Nå hva betyr dette inverse eller motsatte ting?

• $e^x$ lar oss plugge inn tid og få vekst.
• $\ln (x)$ lar oss plugge inn vekst og få tiden det ville ta.

For eksempel:

• $e^3 $ er 20,08. Etter 3 tidsenheter slutter vi med 20.08 ganger hva vi startet med.
• $\ln (20.08) $ er omtrent 3. Hvis vi vil ha vekst på 20.08, vil vi vente 3 tidsenheter (igjen, forutsatt en 100% kontinuerlig vekst).

Med meg? Den naturlige loggen gir oss tiden som trengs for å treffe vår ønskede vekst.

Logaritmisk Aritmetikk er Ikke Normal

du har studert logger før, og de var merkelige dyr. Hvordan gjorde de multiplikasjon til tillegg? Divisjon i subtraksjon? La oss se.

Hva er $\ln (1)$? Intuitivt er spørsmålet: Hvor lenge venter jeg på å få 1x mitt nåværende beløp?

Null. Zip. Nada. Du er allerede på 1x ditt nåværende beløp! Det tar ikke tid å vokse fra 1 til 1.

• $\ln(1) = 0$

Ok, hva med en brøkverdi? Hvor lang tid tar det å få 1/2 mitt nåværende beløp? Forutsatt at du vokser kontinuerlig på 100%, vet vi at $\ln (2)$ er hvor mye tid å doble. Hvis vi reverserer det (dvs. ta den negative tiden), vil vi ha halvparten av vår nåværende verdi.

• $\ln(.5) = – \ln(2)= -.693$

Gir mening, ikke sant? Hvis vi går bakover .693 enheter (negative sekunder, la oss si) vi vil ha halvparten av vårt nåværende beløp. Generelt kan du vende fraksjonen og ta det negative: $\ln(1/3) = – \ ln (3) = -1,09$. Dette betyr at hvis vi går tilbake 1,09 tidsenheter, vil vi ha en tredjedel av det vi har nå.

Ok, hva med den naturlige loggen til et negativt tall? Hvor mye tid tar det å «vokse» bakteriekolonien din fra 1 til -3?

det er umulig! Du kan ikke ha en «negativ» mengde bakterier, kan du? På det meste (er… minst) kan du ha null, men det er ingen måte å ha en negativ mengde av de små critters. Negative bakterier gir bare ikke mening.

• $\ln(\text{negative number}) = \text{undefined}$

Undefined betyr bare «det er ingen tid du kan vente» for å få et negativt beløp. (Vel, hvis vi bruker imaginære eksponentialer, er det en løsning. Men i dag la oss holde det ekte.)

Logaritmisk Multiplikasjon er Mektig Moro

Hvor lang tid tar det å vokse 9x din nåværende mengde? Jo, vi kunne bare bruke ln (9). Men det er for enkelt, la oss være annerledes.Vi kan vurdere 9x vekst som tredobling (tar $\ln (3)$ tidsenheter) og deretter tredoble igjen (tar en annen $ \ ln (3)$ tidsenheter):

• tid til å vokse 9x = $\ln(9)$ = tid til å tredoble og tredoble igjen = $\ln (3) + \ln (3)$

Interessant. Ethvert vekstnummer, som 20, kan betraktes som 2x vekst etterfulgt av 10x vekst. Eller 4x vekst etterfulgt av 5x vekst. Eller 3x vekst etterfulgt av 6.666 x vekst. Ser du mønsteret?

• $\ln (a * b) = \ ln (a) + \ln (b)$

loggen av a ganger b = logg (a) + logg (b). Dette forholdet er fornuftig når du tenker i form av tid til å vokse.Hvis vi ønsker å vokse 30x, kan vi vente $\ln(30)$ alt på en gang, eller bare vente $\ln(3)$, for å tredoble, så vent $\ln (10)$, for å vokse 10x igjen. Nettoeffekten er den samme, så netto tid bør være den samme også(og det er).

hva med divisjon ? $\ln (5/3)$ betyr: Hvor lang tid tar det å vokse 5 ganger og deretter ta 1/3 av det?

vel, voksende 5 ganger er $\ln (5)$. Voksende 1/3 er $- \ ln(3)$ tidsenheter. Så

• $\ln(5/3) = \ln(5) – \ln(3)$

Som sier: Vokse 5 ganger og «gå tilbake i tid» til du har en tredjedel av det beløpet, så du er igjen med 5/3 vekst. Generelt har vi

• $\ln (a/b) = \ln (a) – \ln (b)$

jeg håper den merkelige matematikken til logaritmer begynner å gi mening: multiplikasjon av vekst blir tillegg av tid, deling av vekst blir subtraksjon av tid. Ikke husk reglene, forstå dem.

Ved Hjelp Av Naturlige Logger Med Alle Fall

«Visst,» sier Du, » denne loggen fungerer for 100% vekst, men hva med 5% jeg vanligvis får?»

Det er ikke noe problem. «Tiden» vi kommer tilbake fra $\ln ()$ er faktisk en kombinasjon av hastighet og tid, «x» fra vår $e^x$ ligning. Vi antar bare 100% for å gjøre det enkelt, men vi kan bruke andre tall.

Anta at vi vil ha 30x vekst: plugg inn $\ln (30)$ og få 3,4. Dette betyr:

• $e^x = \text{growth}$
• $e^{3.4} = 30 $

og intuitivt betyr denne ligningen «100% avkastning i 3,4 år er 30x vekst». Vi kan betrakte ligningen som:

vi kan endre «rate» og «time», så lenge rate * time = 3.4. Anta for eksempel at vi vil ha 30x vekst-hvor lenge venter vi på å anta 5% avkastning?

• $\ln(30) = 3,4$
• $ \ text{rate} * \ text{time} = 3.4$
• $.05 * \tekst{tid} = 3,4$
• $ \ tekst{tid} = 3,4/.05 = 68 \ text{years}$

Intuitivt tror Jeg » $\ln (30) = 3,4$, så ved 100% vekst vil det ta 3,4 år. Hvis jeg dobler veksten, halverer jeg tiden som trengs.»

• 100% i 3,4 år = 1,0 * 3,4 = 3,4
• 200% i 1,7 år = 2,0 * 1,7 = 3,4
• 50% i 6,8 år = 0,5 * 6,8 = 3,4
• 5% i 68 år = .05 * 68 = 3.4

Kult, eh? Den naturlige loggen kan brukes med hvilken som helst rente eller tid så lenge produktet er det samme. Du kan vri variablene alt du vil.

Fantastisk eksempel: Regelen på 72

Regelen på 72 er en mental matte snarvei for å estimere tiden som trengs for å doble pengene dine. Vi kommer til å utlede det (yay!) og enda bedre, vi skal forstå det intuitivt .

Hvor lang tid tar det å doble pengene dine på 100% rente, forsterket hvert år?

Uh oh. Vi har brukt naturlig logg for kontinuerlige priser, men nå ber du om årlig interesse? Vil ikke dette ødelegge vår formel? Ja, det vil, men til rimelige renter som 5%, 6% eller til og med 15%, er det ikke mye forskjell mellom årlig sammensatt og fullt kontinuerlig interesse. Så den grove formelen virker grovt, og vi vil late som om vi får full kontinuerlig interesse.

nå er spørsmålet enkelt: Hvor lenge skal du doble med 100% rente? ln (2) = .693. Det tar .693 tidsenheter (år, i dette tilfellet) for å doble pengene dine med kontinuerlig sammensetning med en hastighet på 100%.

Ok, hva om vår interesse ikke er 100% Hva om det er 5% eller 10%?

Enkel. Så lenge rente * tid = .693, vi dobler pengene våre:

• rate * tid = .693
• tid = .693/rate

Så, hvis vi bare hadde 10% vekst, ville det ta .693 / .10 eller 6,93 år å doble.

for å forenkle ting, la oss multiplisere med 100 slik at vi kan snakke om 10 i stedet for .10:

• tid til dobbel = 69,3 / sats, hvor sats antas å være i prosent.

nå er tiden for å doble med 5% vekst 69,3/5 eller 13,86 år. 69,3 er imidlertid ikke det mest delbare tallet. La oss velge en nær nabo, 72, som kan deles med 2, 3, 4, 6, 8 og mange flere tall.

• tid til dobbel = 72 / rate

som er regelen av 72! Lett breezy.

Hvis du vil finne tid til å tredoble, vil du bruke ln(3) ~ 109.8 og få

• tid til triple = 110 / rate

Som er en annen nyttig tommelfingerregel. 72-Regelen er nyttig for renter, befolkningsvekst, bakteriekulturer og alt som vokser eksponentielt.

hvor skal du herfra?

jeg håper den naturlige loggen gir mer mening – den forteller deg tiden som trengs for en eksponentiell vekst. Jeg anser det som» naturlig «fordi e er den universelle vekstraten, så ln kan betraktes som den «universelle» måten å finne ut hvor lang tid det tar å vokse.

Når du ser $\ln (x)$, tenk bare «hvor mye tid å vokse til x». I neste artikkel vil vi bringe e og ln sammen, og den søte duften av matte vil fylle luften.

Tillegg: Den Naturlige Loggen Til E

Hurtig quiz: Hva er $\ln (e)$?

• mattroboten sier: fordi de er definert som inverse funksjoner, klart $\ln (e) = 1$
• det intuitive mennesket: ln (e) er hvor lang tid det tar å få «e» vekstenheter (ca 2.718). Men e er mengden vekst etter 1 tidsenhet, så $\ln (e) = 1$.

Tenk intuitivt.

Andre Innlegg i Denne Serien

1. En Intuitiv Guide Til Eksponentielle Funksjoner& e
2. Demystifying Den Naturlige Logaritmen (ln)
3. En Visuell Guide Til Enkle, Sammensatte Og Kontinuerlige Renter
4. Vanlige Definisjoner av E (Farget)
5. Forstå Eksponenter (Hvorfor 0^0 = 1?)
6. Bruke Logaritmer i Den Virkelige Verden
7. Hvordan Tenke Med Eksponenter og Logaritmer
8. Forstå Diskret vs. Kontinuerlig Vekst
9. Hva betyr en eksponent egentlig?
10. Q: Hvorfor er e spesiell? (2.718…, ikke 2, 3,7 eller et annet nummer?)