i andre seksjoner ble det nevnt at mange av egenskapene til faste stoffer, væsker og gasser kan regnskapsføres hvis vi antok at stoffer er laget av atomer eller molekyler som stadig er i bevegelse. Boyles lov og de andre gassloven har nå gitt oss mye mer kvantitativ informasjon om gasser, og det er verdt å spørre om med den forrige modellen kan vi gjøre kvantitative spådommer i samsvar med disse lovene. Når vi svarer på dette spørsmålet, vil vi også få viktig innsikt i temperaturens og varmeenergiens natur.den mikroskopiske teorien om gassadferd basert på molekylær bevegelse kalles kinetisk teori om gasser. Dens grunnleggende postulater er oppført i Tabell 1:

TABELL \(\PageIndex{1}\) Postulater Av Den Kinetiske Teorien Om Gasser.

1 molekylene i en gass er små og svært langt fra hverandre. Det meste av volumet som en gass opptar er tomt rom.

2 Gassmolekyler er i konstant tilfeldig bevegelse. Like mange molekyler beveger seg i en retning som i alle andre.

3 Molekyler kan kollidere med hverandre og med veggene i beholderen. Kollisjoner med veggene står for trykket av gassen.

4 når kollisjoner oppstår, mister molekylene ingen kinetisk energi; det vil si at kollisjonene sies å være perfekt elastiske. Den totale kinetiske energien til alle molekylene forblir konstant med mindre det er noen utvendig forstyrrelse med

5 molekylene utøver ingen attraktive eller repulsive krefter på hverandre unntatt under kollisjonsprosessen. Mellom kollisjoner beveger de seg i rette linjer.

Fra dem er det mulig å utlede følgende uttrykk for trykket av en gass når det gjelder egenskapene til molekylene:

\ hvor P, V = trykk og volum av gassen

N = antall molekyler

m = masse av hvert molekyl

(u2)ave = gjennomsnittlig (eller gjennomsnittlig) av kvadratene av alle individuelle molekylhastigheter. Denne gjennomsnittlige kvadrathastigheten må brukes fordi trykket er proporsjonalt med kvadratet av molekylhastighet, og molekylære kollisjoner forårsaker at forskjellige molekyler har ganske forskjellige hastigheter.

Snarere enn om oss selv med prosedyren for å utlede Eq. \(\ref{1}\), la oss inspisere ligningen og se at dens generelle funksjoner er mye som vi forventer. På noen måter er evnen til å gjøre dette med en formel mer nyttig enn evnen til å utlede den. Figur \(\PageIndex{1}\)

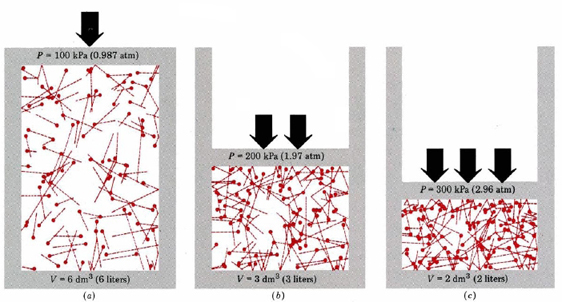først av alt forteller ligningen oss at trykket av en gass er proporsjonalt med antall molekyler dividert med volumet. Dette vises grafisk I Figur \(\PageIndex{1}\), hvor en datamaskin har trukket det samme antall gassmolekyler som opptar hver av tre forskjellige volumer. «Halen» på hvert molekyl viser den nøyaktige banen etterfulgt av molekylet i forrige mikrosekund – jo lengre halen, desto raskere gikk molekylet. Gjennomsnittet av kvadratene av halelengdene er proporsjonal med (u2) ave og er det samme i alle tre diagrammer. Det antas også at alle molekylene har like masser.

som du kan se, reduserer volumet av gassen antall kollisjoner per arealenhet på beholderens vegger. Hver kollisjon utøver kraft på veggen; kraft per arealenhet er trykk, og så er antall kollisjoner per arealenhet proporsjonal med trykk. Halvering av volumet dobler trykket, en prediksjon som stemmer overens Med eksperimentelle fakta oppsummert I Boyles lov. Ligning \(\ref{1}\) sier også at trykket er proporsjonalt med massen av hvert gassmolekyl. Igjen, dette er hva vi forventer. Tunge molekyler gir en større «push» (den tekniske termen for dette er impuls) mot veggen enn lys med samme hastighet.

endelig forteller ligningen oss at trykket er proporsjonalt med gjennomsnittet av kvadratene av molekylhastighetene. Denne avhengigheten av hastigheten er rimelig hvis vi innser at dobling av hastigheten til et molekyl har to effekter.for Det Første kan molekylet bevege seg lenger i en gitt tidsperiode, og fordoble antall kollisjoner med veggene. Det vil doble presset. For det andre dobler doble hastigheten til et molekyl push eller impuls av hver kollisjon. Dette dobler trykket igjen. Derfor dobler et molekyls hastighet trykket, og For et stort antall molekyler Er P proporsjonal med gjennomsnittlig kvadrathastighet.