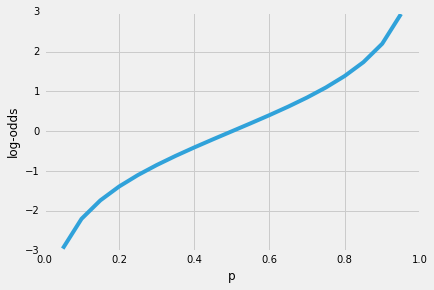
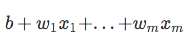だから、ロジスティック回帰の素晴らしい特性の一つは、シグモイド関数が予測の条件付き確率、クラス確率を出力することです。 それはどのように動作しますか?いわゆる”オッズ比”p/(1-p)から始めましょう。p|(1-p)は、特定の正のイベントが発生する確率と発生しない確率との比を表します。p(y=1/x)は、”予測したいイベント”、すなわちp(y=1/x)を指します。
(ロジスティック回帰は特殊な種類のシグモイド関数であり、ロジスティックシグモイド;他のシグモイド関数、例えば双曲線正接が存在することに注意してください)。したがって、正のイベントが発生する可能性が高いほど、オッズ比が大きくなります。
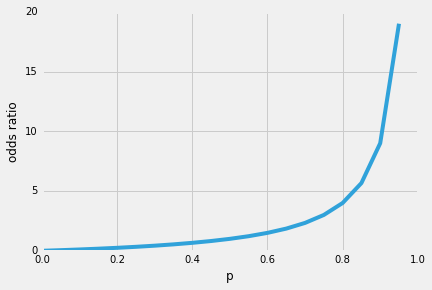
正のイベントが発生する可能性が高いほど、オッズ比が大きくなります。ここで、このオッズ比の自然対数、log-oddsまたはlogit関数を取ると、次のようになります。
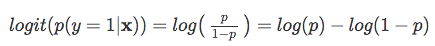
次に、このログ変換を使用して、説明変数とターゲット変数との関係をモデル化しましょう。
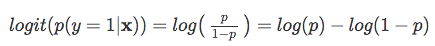

次に、このログ変換を使用して、説明変数とターゲット変数との関係をモデル化しましょう。
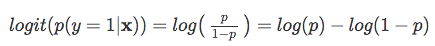
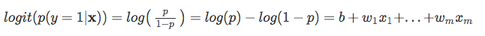
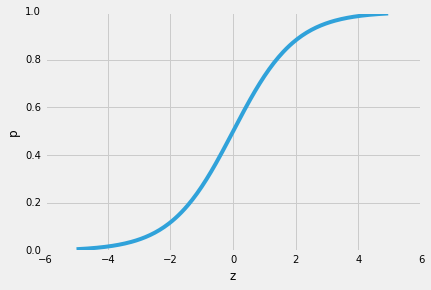
| さて、*P(y=1 | x)*は私たちが本当に興味を持っているものなので、上記の方程式の右の部分を予測しようとしてい So, let’s take the inverse of this logit function … et viola, we get the logistic sigmoid: |
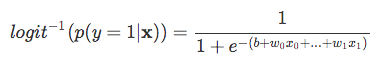
| which returns the class probabilities *p(y=1 | x)* from the inputs |