ボイルの法則
ロバート-ボイル(1627-1691)、英語の化学者は、広く化学の近代的な実験科学の創始者の一人であると考えられている。 彼は、密閉されたガスのサンプルの圧力を2倍にしながら、その温度を一定に保つことによって、ガスの体積が半分に減少することを発見した。 ボイルの法則は、温度が一定に保たれているとき、与えられた質量のガスの体積は圧力と反比例して変化すると述べている。 このようにして逆の関係が記述されます。 一方の変数の値が増加すると、もう一方の変数は減少します。物理的には、何が起こっていますか?
ガス分子は移動しており、互いに一定の距離を離れています。 圧力の増加は、分子をより近くに押し込み、体積を減少させる。 圧力が低下すると、ガスはより大きな体積で自由に移動します。P>

数学的には、ボイルの法則は次の式で表すことができます:\(k\)は、与えられたガスのサンプルの定数であり、ガスの質量と温度にのみ依存します。
\(k\)は、ガスの質量と温度にのみ依存します。
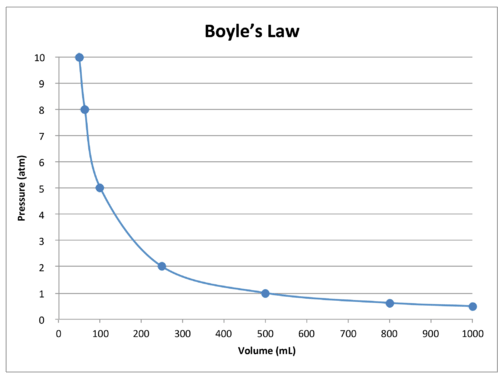
\(k\)は、\(k\)は、\(k\)は、\(k\)は、 下の表は、一定温度での一定量のガスの圧力と体積のデータを示しています。 3番目の列は、このデータの定数\(\left(k\right)\)の値を表し、常に圧力に体積を掛けた値に等しくなります。 変数の1つが変更されると、他の変数は\(P\times V\)の積が常に同じままになるように変更されます。 この特定のケースでは、その定数は\(500\:\text{atm}\cdot\text{mL}\)です。
| Pressure \(\left( \text{atm} \right)\) | Volume \(\left( \text{mL} \right)\) | \(P \times V = k\) \(\left( \text{atm} \cdot \text{mL} \right)\) |
|---|---|---|
| 0.5 | 1000 | 500 |
| 0.625 | 800 | 500 |
| 1.0 | 500 | 500 |
| 2.0 | 250 | 500 |
| 5.0 | 100 | 500 |
| 8.0 | 62.5 | 500 |
| 10.0 | 50 | 500 |
テーブル内のデータのグラフは、ボイルの法則(下の図を参照)。 体積は\(x\)軸にプロットされ、対応する圧力は\(y\)軸にプロットされます。P>
ボイルの法則は、ガスの変化する条件を比較するために使用することができます。 我々は、ガスの初期圧力と初期体積を表すために\(P_1\)と\(V_1\)を使用します。 変更が行われた後、\(P_2\)と\(V_2\)は最終的な圧力と体積を表します。 ボイルの法則の数学的関係は次のようになります。
\
この方程式は、他の三つが知られている場合、四つの量のいずれかを計算するために使用できます。例\(\PageIndex{1}\)
酸素ガスのサンプルの体積は\(425\)です。
酸素ガスのサンプルの体積は\(425\)です。
酸素ガスのサンプルの体積は\(425\)です。
: 圧力が\(387\:\text{kPa}\)に等しいとき。 ガスは\(1.75\:\text{L}\)コンテナに展開することができます。 ガスの新しい圧力を計算します。ステップ1:既知の数量を一覧表示し、問題を計画します。
解決策
ステップ1:既知の数量を一覧表示し、問題を計画します。
\(P_1=387\:\text{kPa}\)
不明
- \(v_2=1.75\:\text{L}=1750\:\text{mL}\)
- \(v_2=1.75\:\text{L}=1750\:\text{mL}\)
- \(v_2=1.75\:\text{L}=1750\:\text{mL}\)
- \(v_2=1.75\:\text{L}=1750\p_2=? \:\text{kPa}\)
ボイルの法則を使って未知の圧力\(\left(P_2\right)\)を解きます。 2つのボリューム(\(V_1\)と\(V_2\))は同じ単位で表現されるので、\(V_2\)は\(\text{mL}\)に変換されていることが重要です。ステップ2:解決します。
ステップ2:解決します。
まず、\(P_2\)を解くために方程式を代数的に再配置します。
\
ここで、既知の量を方程式に代入して解きます。ステップ3:結果について考えてみてください。
ボリュームは元の値の4倍をわずかに超えるように増加しているため、圧力は約四分の一減少しています。 圧力は\(\text{kPa}\)であり、値には3つの有効数字があります。 問題全体を通して一貫している限り、任意の圧力または体積単位を使用できることに注意してください。div