原子軌道

軌道はボーアの軌道の量子力学的微細化です。 彼の半径が固定された単純な円軌道の概念とは対照的に、軌道は電子を持つ確率が異なる空間の数学的に導出された領域である。

電子確率分布を表現する一つの方法は、水素の1s軌道に対する図6.5.2に示されています。 Σ2は与えられた体積の空間（立方ピコメーターなど）で電子を見つける確率を与えるので、Σ2対核からの距離（r）のプロットは確率密度のプロットである。 1s軌道は球対称であるため、任意の点で1s電子を見つける確率は、核からの距離にのみ依存します。 確率密度はr=0（核）で最大であり、距離の増加とともに着実に減少する。 Rの値が非常に大きい場合、電子確率密度は非常に小さいがゼロではない。これとは対照的に、半径r1、r2、r3、…、rx−1、rxの一連のx球状シェル上のすべての点にある電子の確率を加算することにより、半径確率（核からの距離rで1s電子を見つける確率）を計算することができます。 実際には、タマネギの層（図\(\PageIndex{1}\)の部分（a））のように、原子を非常に薄い同心円状の殻に分割し、各球状の殻に電子を見つける確率を計算しています。 電子確率密度はr=0で最大であることを思い出してください（図\(\PageIndex{1}\)の部分（b））ので、ドットの密度は、図\(\PageIndex{1}\)の部分（a）の最小の球状殻で最大です。 対照的に、各球状殻の表面積は4π r2に等しく、これはrの増加とともに非常に急速に増加する（図\(\PageIndex{1}\)の部分（c））。 球状殻の表面積は、電子確率密度が減少するよりもrの増加とともに急速に増加するので、半径方向確率のプロットは、特定の距離で最大を有する（図\(\PageIndex{1}\)の部分(d)）。 最も重要なのは、rが非常に小さいとき、球状殻の表面積は非常に小さく、核に近い電子を見つける確率は非常に低く、核では電子確率は消滅する（図\(\PageIndex{1}\)の部分(d)）。

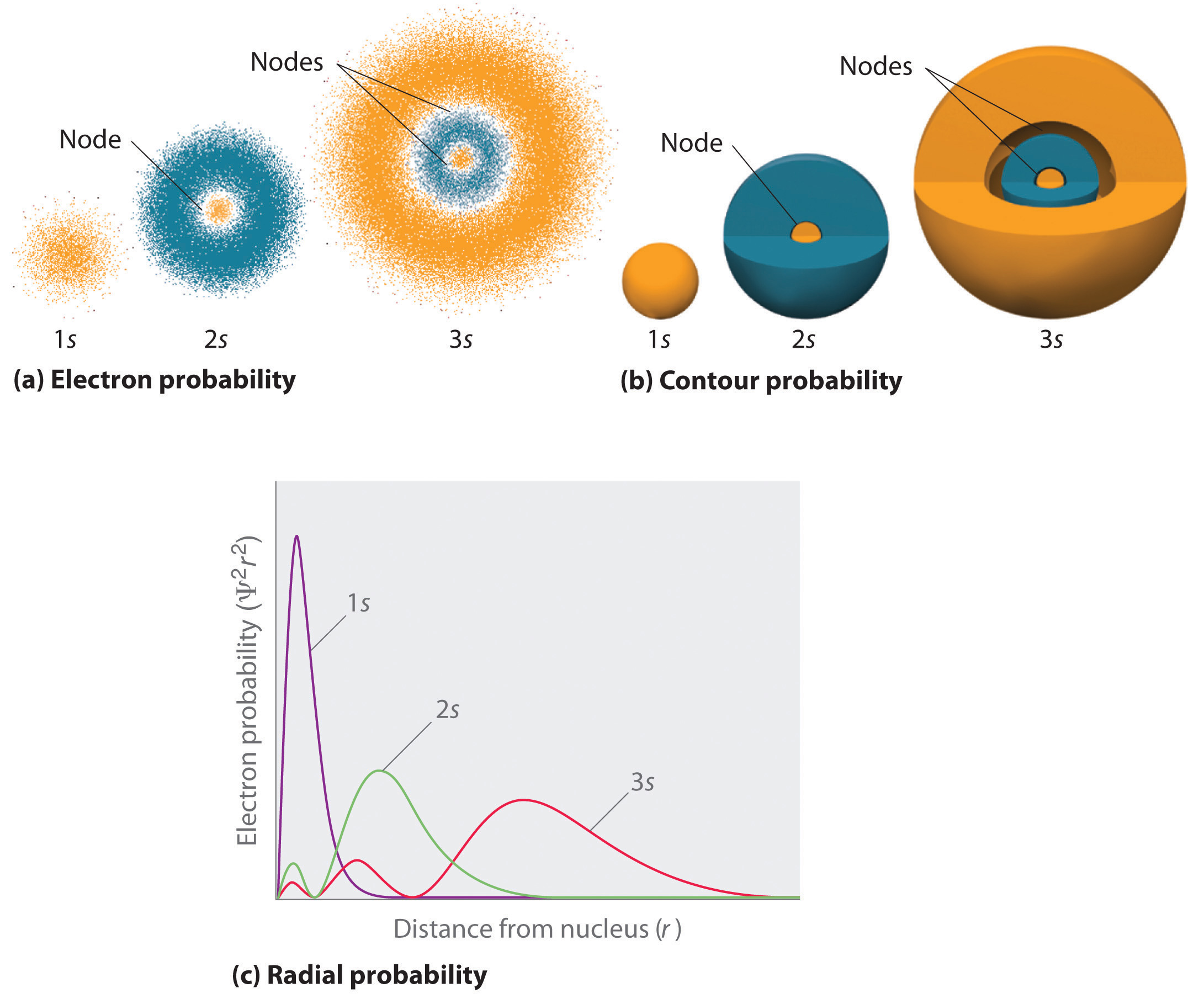
水素原子の場合、半径方向確率プロットのピークはr=0.529Å（52.9pm）で発生し、これはボーアによってn=1軌道で計算された半径である。 したがって、量子力学から得られる最も可能性の高い半径は、古典力学によって計算された半径と同一である。 しかし、ボーアのモデルでは、電子は時間の100％この距離にあると仮定されていたが、量子力学的シュレーディンガーモデルでは、この距離には時間の一部しかないと仮定されていた。 二つのモデルの違いは電子の波状挙動とＨｅｉｓｅｎｂｅｒｇ不確かさ原理に起因する。図\(\PageIndex{2}\)は、水素1s、2s、および3s軌道の電子確率密度を比較します。 3つはすべて球対称であることに注意してください。 しかし、2s軌道と3s軌道では（および他のすべてのs軌道でも）、電子確率密度はrの増加とともに滑らかに落ちることはありません。 最小値は、非ゼロ電子確率の球状領域と交互に球状ノード（ゼロ電子確率の領域）に対応する。P>