学習目標
このセクションの終わりまでに、あなたは次のことができるようになります。
- 重力に対して行われた作業の観点から重力ポテンシャルエネルギーを説明します。
- は、地球上の高さhの質量mの物体の重力ポテンシャルエネルギーがPEg=mghによって与えられることを示しています。
- 位置の関数としてのポテンシャルエネルギーの知識が計算を簡素化し、物理現象を説明するために使用することができる方法を示しています。
重力に対して行われた作業
階段を登るとオブジェクトを持ち上げることは、科学的および日常的な意味での作業です—それは重力に対 仕事があるとき、エネルギーの変換があります。 重力に対して行われた作業は、我々はこのセクションで探求する蓄積されたエネルギーの重要な形になります。

図1。 (a)重量を持ち上げるために行われた作業は、重力ポテンシャルエネルギーとして質量-地球システムに保存されます。 (b)重量が下方に移動すると、この重力ポテンシャルエネルギーは鳩時計に転送されます。
図1のように、質量mの物体を高さhを通して持ち上げる作業を計算しましょう。 物体が一定の速度でまっすぐに持ち上げられる場合、それを持ち上げるのに必要な力はその重量mgに等しい。 質量で行われる作業は、W=Fd=mghです。 これは、物体-地球システムに入れられる(またはそれによって得られる)重力ポテンシャルエネルギー(PEg)であると定義します。 このエネルギーは、重力によってお互いを引き付ける2つの物体間の分離状態に関連しています。 便宜上、これは地球の重力場に蓄積されたエネルギーであることを認識して、これを物体によって得られたペグと呼ぶ。 なぜ私たちは”システム”という言葉を使うのですか? ポテンシャルエネルギーは、その物理的な位置のために、単一のオブジェクトではなくシステムの特性です。 オブジェクトの重力ポテンシャルは、地球-オブジェクトシステム内の周囲に対するその位置によるものです。 オブジェクトに加えられる力は、システムの外部からの外力です。 それが肯定的な仕事をするときそれはシステムの重力の潜在的なエネルギーを高める。 重力ポテンシャルエネルギーは相対位置に依存するため、ポテンシャルエネルギーを0に等しく設定するための基準レベルが必要です。 私たちは通常、地球の表面であることをこの点を選択しますが、この点は任意です;この違いは、行われた作業に関連するものであるため、重要なのは、引 はしごの2つのラング間の(地球-物体系における)物体の重力ポテンシャルエネルギーの差は、最後の2つのラングと最初の2つのラングで同じにな
ポテンシャルエネルギーと運動エネルギーの間の変換
重力ポテンシャルエネルギーは、運動エネルギーなどの他の形態のエネルギーに変換 質量を解放すると、重力はその上でmghに等しい量の仕事を行い、それによってその運動エネルギーを同じ量だけ(仕事エネルギー定理によって)増加させ 作業の中間ステップを明示的に考慮せずに、PEgからKEへの変換だけを検討する方がより有用であることがわかります。 (例2を参照。)このショートカットは、明示的に力を使用するのではなく、エネルギー(可能であれば)を使用して問題を解決することを容易にします。より正確には、重力ポテンシャルエネルギーの変化Δ PegをΔ Peg=mghと定義し、ここで、簡単にするために、通常のΔ Hではなくhで高さの変化を表す。 Hは、最終的な高さが初期の高さよりも大きい場合は正であり、その逆も同様であることに注意してください。 例えば、カッコウ時計から吊るされた0.500kgの質量が1を上げるとする。00m、重力ポテンシャルエネルギーの変化は
\begin{array}{lll}mgh&&(0.500\text{kg})(9.80\text{m/s}^2)(1.00\text{m})4.90\text{kg}\cdot\text{m}^2\text{/s}^2=4.90\text{j}\end{array}\\
重力ポテンシャルエネルギーの単位はジュールであり、仕事や他のエネルギーの単位と同じであることに注意してくださ クロックが実行されると、質量が低下します。 私たちは、質量を徐々にその4を放棄すると考えることができます。直接仕事をする重力の力を考慮しないで重力の潜在的なエネルギーの90J。
計算を簡素化するために潜在的なエネルギーを使用して

点Aと点Bの間の重力ポテンシャルエネルギー(Δ Peg)の変化は経路とは無関係である。式Δ Peg=mghは、質量がまっすぐ上に持ち上げられたときだけでなく、高さがhの変化を持つ任意の経路に適用されます。
式Δ Peg=mghは、高さがhの変化を持 (図2を参照してください。)複雑な経路に沿って行われた作業を計算するよりも、mgh(単純な乗算)を計算する方がはるかに簡単です。 重力ポテンシャルエネルギーの考え方は、それが非常に広く適用可能であり、計算を容易にするという二重の利点を有する。
これからは、質量mの垂直位置hの変化は重力ポテンシャルエネルギー mghの変化を伴うと考え、重力によって行われる作業を計算するという同等ではあるがより困難な作業を避けることになる。2つの点の間の任意のパスについてΔ Peg=mgh。 重力は、力によって、または力に対して行われる作業は、それらの間のパスではなく、開始点と終了点にのみ依存する小さなクラスの力の一つです。
例1. 落下を停止する力
A60。彼は(彼の膝関節が0.500センチメートル圧縮して)堅く着陸した場合、膝関節の力を計算します。
戦略
この人のエネルギーは、彼が停止すると床によって彼に行われた作業によって、このような状況ではゼロになります。 彼が落ちると、最初のペグはKEに変換されます。 床によってできている仕事はゼロにこの運動エネルギーを減らす。
ソリューション
彼が停止するように床によって人に行われた作業は、w=Fd cos θ=−Fdで与えられ、停止中の変位と床からの力が反対方向にあるため、マイナス記号で与えられる(cos θ=cos180θ=-1)。 床はシステムからエネルギーを除去するので、負の仕事をします。人が床に到達したときに有する運動エネルギーは、高さh:KE=−Δ Peg=−mghを通って落下することによって失われる潜在エネルギーの量である。
人が床に到達したときに有する運動エネルギーは、高さhを通って落下することによって失われる潜在エネルギーの量である。
人の膝が曲がる距離dは、落下の高さhよりもはるかに小さいので、膝の曲がり中の重力ポテンシャルエネルギーの追加の変化は無視されます。
人の床によって行われた作業Wは人を停止させ、人の運動エネルギーをゼロにします:W=−KE=mgh。この式をWの式と組み合わせると、−Fd=mghが得られます。
この式をWの式と組み合わせると、-Fd=mghが得られます。
人が倒れたのでhが負であることを思い出して、膝関節への力は次のように与えられます。
\displaystyle{F}=-\frac{mgh}{d}=-\frac{\left(60。0\text{kg}\right)\left(9.80\text{m/s}^2\right)\left(-3.00\text{m}\right)}{5.00\times10^{-3}\text{m}}=3.53\times10^5\text{N}\\
ディスカッション
このような大きな力(人の体重の500倍以上)は、短い衝撃時間にわたって骨を壊すのに十分です….. 衝撃を緩和するためのはるかに良い方法は、脚を曲げたり地面を転がしたりして、力が作用する時間を長くすることです。 このようにして0.5mの曲げ運動を行うと、この例よりも100倍小さい力が得られます。 カンガルーのホッピングは、この方法が実際に行われていることを示しています。 カンガルーは移動のためにホッピングを使用する唯一の大きな動物ですが、ホッピングの衝撃は、各ジャンプでの後肢の屈曲によって緩和されます。 (図3を参照してください。)

図3. カンガルーの上に地面によって行われた作業は、それが着陸すると、その運動エネルギーをゼロに減少させます。 しかし、より長い距離にわたって後肢に地面の力を加えることによって、骨への影響が低減される。 (クレジット:クリスサミュエル、Flickr)
例2。 ジェットコースターの高さからジェットコースターの速度を求める
- 図4に示すジェットコースターの最終速度は、20.0mの丘の頂上で休息から始まり、摩擦力
- 初期速度が5.00m/sの場合、その最終速度は何ですか(再び無視できる摩擦を仮定して)?
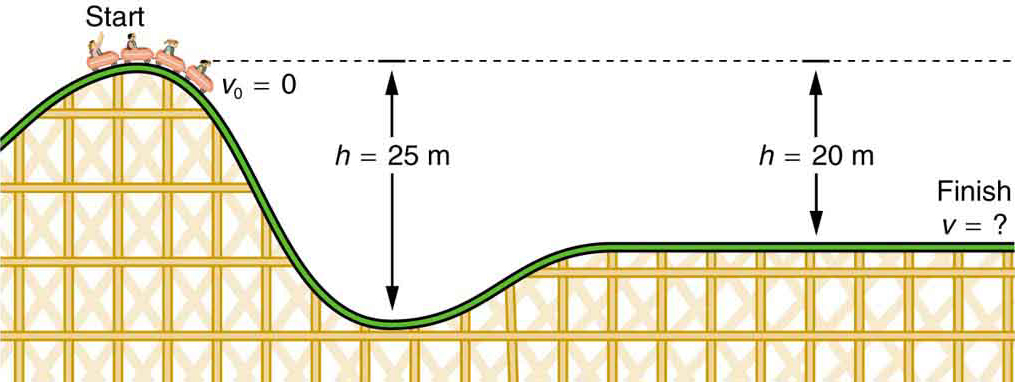
図4. ジェットコースターの速度は、重力がそれを下り坂に引っ張り、その最低点で最大になるにつれて増加する。 エネルギーの観点から見ると、ジェットコースター-地球システムの重力ポテンシャルエネルギーは運動エネルギーに変換されます。 摩擦によって行われた作業が無視できる場合、すべてのΔ PegはKEに変換されます。
戦略
ジェットコースターは下り坂になると潜在的なエネルギーを失います。 私たちは摩擦を無視するので、トラックによって加えられる残りの力は、動きの方向に垂直であり、仕事をしない法線力である。 ジェットコースターの純仕事は単独で重力によってそれからされる。 距離hを通って下方に移動することによる重力ポテンシャルエネルギーの損失は、運動エネルギーの利得に等しい。 これは、−Δ Peg=Δ KEのように式の形で書くことができます。 PEgとKEの方程式を使用して、目的の量である最終速度vを解くことができます。ここで、初期運動エネルギーはゼロであるため、\Delta\text{KE}=\frac{1}{2}mv^2\となります。 ポテンシャルエネルギーの変化の方程式は、Δ Peg=mghであると述べている。 この場合、hは負であるため、マイナス記号を明確に示すために、これをΔ Peg=−mg|h|と書き直します。 したがって、-Δ Peg=Δ KEはmg|h|=\frac{1}{2}{mv}.2\\になります。vを解くと、質量が相殺され、v=\sqrt{2g|h|}\\がわかります。\begin{array}{lll}v&&&\sqrt{2\left(9.80\text{m/s}^2\right)\left(20.0\text{m}\right)}\テキスト{}&&19.8\テキスト{m/s}端{アレイ}\\
パート2のためのソリューション
再び−δ peg=δ ke。 この場合、初期運動エネルギーがあるので、
\Delta\text{KE}=\frac{1}{2}mv^2-\frac{1}{2}mv_0^2\。したがって、mg|h|=\frac{1}{2}mv^2-\frac{1}{2}mv_0^2\です。再配置すると、\frac{1}{2}mv^2=mg|h|+\frac{1}{2}mv+0^2\になります。これは、最終的な運動エネルギーが最初の運動エネルギーと重力ポテンシャルエネルギーの合計であることを意味します。
これは、最終的な運動エネル 質量は再び相殺され、v=\sqrt{2g|h|+v_0^2}\\となります。この方程式は運動学方程式v=\sqrt{v_0^2+2ad}\\と非常によく似ていますが、より一般的です—運動学方程式は一定の加速度に対してのみ有効ですが、上の式は ここで、既知の値を代入すると、
\begin{array}{lll}v&&\sqrt{2\left(9.80\text{m/s}^2\right)\left(20.0\text{m}\right)+\left(20.0\text{m}\right)+\left(20.0\text{m}\right)+\left(20.0\text{m}\right)+\left(20.0\text{m}\right)+\left(20.0\text{m}\right)+\left(20.0\text{m}\right)+\left(20.0\text{m}\right)+\left(20.0\text{m}\right5.00\text{m/s}\right)^2}\\\text{}&&20。4\text{m/s}\end{array}\\
議論と含意
まず、質量がキャンセルされることに注意してください。 これは、摩擦が無視できる場合、すべての物体が同じ速度で落下する落下物体で行われた観測と非常に一致しています。 第二に、ジェットコースターの速度のみが考慮され、どの時点でもその方向に関する情報はありません。 これは別の一般的な真実を明らかにする。 摩擦が無視できる場合、落下体の速度は、その初期速度および高さにのみ依存し、その質量または経路には依存しない。 例えば、ジェットコースターは、まっすぐに20.0m落ちるか、図のようなより複雑なパスを取るかにかかわらず、同じ最終速度を持つことになります。 第三に、そしておそらく予想外に、パート2の最終的な速度はパート1よりも大きくなりますが、5.00m/sよりもはるかに小さいことに注意してください。
重力によって、または重力に対して行われる作業は、開始点と終了点にのみ依存し、間のパスには依存しないことがわかりました。 我々はいくつかの他の力のために同じことを行うことができ、我々はこれがエネルギー保存の法則の正式な定義につながることがわかります。
接続を作る:持ち帰り調査-電位を運動エネルギーに変換する
この実験では、重力ポテンシャルエネルギーの運動エネルギーへの変換を調 滑らかで水平な表面に、その長さに沿って溝が走っている種類の定規と本を使用して傾斜を作ります(図5を参照)。 定規の10cmの位置に大理石を置き、定規を転がしてみましょう。 それはレベルの表面に当たったとき、それは一メートルをロールバックするのにかかる時間を測定します。 今度は20cmおよび30cmの位置に大理石を置き、再度水平な表面の1つのmを転がすために取る時を測定しなさい。 すべての3つの位置のレベルの表面上の大理石の速度を見つけます。 大理石が移動した距離に対する速度の二乗をプロットします。 各プロットの形状は何ですか? 形状が直線である場合、プロットは、底部の大理石の運動エネルギーが放出点でのポテンシャルエネルギーに比例することを示しています。

図5. 大理石は定規を転がし、水平表面上の速度が測定されます。
セクションの概要
- オブジェクトを持ち上げる際に重力に対して行われた作業は、オブジェクト-地球システムの潜在的なエネル重力ポテンシャルエネルギーの変化Δ PegはΔ Peg=mghであり、hは高さの増加であり、gは重力による加速度である。
- 地球の表面近くの物体の重力ポテンシャルエネルギーは、質量-地球システム内のその位置によるものです。 重力ポテンシャルエネルギー Δ Pegの違いだけが物理的な意義を持っています。
- 物体が摩擦なしで下降すると、その重力ポテンシャルエネルギーは速度の増加に応じて運動エネルギーに変化し、Δ KE=−Δ Peg
概念的な質問
- 例2では、高さ20mを下り、初速が5m/sのジェットコースターの最終速度を計算した。 ジェットコースターの初期速度が5m/sの上り坂ではなく、上り坂でコーストし、停止してから、スタートより20m下の最終地点までロールバックしたとします。 その場合、同じ最終速度を持っていたことがわかります。 エネルギーの保存の観点から説明します。
- 本を棚に持ち上げるときに行う作業は、取られた道に依存しますか? かかった時間に? 棚の高さに? 本の質量に?
問題&演習
- 水力発電施設(図6参照)は、ダムの背後にある水の重力ポテンシャルエネルギーを電気エネルギーに変換します。 (a)体積50の湖の発電機に対する重力ポテンシャルエネルギーは何ですか。0km3(質量=5.00×1013kg)、湖の平均高さが発電機の上に40.0mであることを考えると? (b)これを9メガトンの核融合爆弾に蓄えられたエネルギーと比較してください。

図6. 水力発電施設(クレジット:Denis Belevich、Wikimedia Commons)
- (a)その質量が約7×109kgで、質量の中心が36であることを考えると、Cheopsの大ピラミッドに(それが構築されている地面周囲の地面の上の5つのmか。 (b)このエネルギーは、人の毎日の食物摂取量とどのように比較されますか?
- 350gのkookaburra(大きなカワセミの鳥)が75gのヘビを拾い上げ、地面から枝まで2.5m上げたとします。 (a)鳥はヘビにどのくらいの仕事をしましたか? (b)それ自身の重心を枝に上げるためにどれくらいの仕事をしましたか?
- 例2では、20.0m降下したジェットコースターの速度は、初期速度が5.00m/sの場合、静止から開始したときよりもわずかに大きいことがわかりました。 これは、Δ PE>>KEiであることを意味します。 KEIに対するΔ PEの比を取ることによって、この文を確認します。 (質量がキャンセルされることに注意してください。)
- 100gのおもちゃの車は、それが動き始める圧縮されたばねによって推進されます。 車は図7の湾曲したトラックに従います。 おもちゃの車の最終速度が0.687m/sの場合、その初期速度が2.00m/sであり、摩擦のない斜面を海岸し、高度が0.180mを獲得することを示します。

図7. おもちゃの車は傾斜したトラックを上に移動します。 (credit:Leszek Leszczynski,Flickr)
- 下り坂のスキーレースでは、驚くべきことに、ランニングスタートを得ることによって利点はほとんど得られません。 (これは、小さな丘でも重力ポテンシャルエネルギーのゲインに比べて初期運動エネルギーが小さいためです。)これを実証するために、摩擦を無視して70.0mの30º斜面に沿って空を飛ぶスキーヤーのためにかかった最終速度と時間を見つけます:(a)休息から始ま (b)2.50m/sの初期速度から始まります。(c)答えはあなたを驚かせますか? それはまだ非常に競争力のあるイベントで実行中のスタートを取得することが有利である理由を議論します。
用語集
重力ポテンシャルエネルギー:オブジェクトが重力場での位置に起因するエネルギー
問題に対する選択された解&演習
1。 (a)1.96×1016J;(b)湖の重力ポテンシャルエネルギーと爆弾に蓄えられたエネルギーの比は0.52である。 つまり、湖に蓄えられたエネルギーは、9メガトンの核融合爆弾の約半分です。
3. (a)1.8J;(b)8.6J
5. {v}_{f}=\sqrt{2gh+{v_0}^2}=\sqrt{2\left(9.80\text{m/s}^2\right)\left(-0.180\text{m}\right)+\left(2.00\text{m/s}\right)2 2}=0.687\text{m/s}\