このセクションでは、カバーしています:
- 区分的関数の紹介
- 区分的関数を評価する
- 区分的関数をグラフ化する
- 区分的関数が連続的または非連続的であるかどうかを知る方法
- 区分的関数グラフから方程式を得る
- 区分的関数としての絶対値
- 区分的関数の変換
- 区分的関数ワード問題
- より多くの練習

区分的関数(またはピース単位の関数)は、名前が付けられているものです: すべて1つのグラフ上の異なる関数(サブ関数)の部分。 それらを考える最も簡単な方法は、グラフ上に複数の関数を描画し、それらが想定されていない関数の一部を消去した場合です(\(x\)に沿って)。\(x\)の異なる区間に対して異なって定義されています。 \(y\)は\(x\)の異なる値に対して異なって定義されています。\(x\)を使用してどの間隔にあるかを調べるので、\(y\)が何であるかを知ることができます。\(y\)は、\(x\)の値が\(x\)であることになっています。\(y\)は、\(x\)の値が\(x\
区分的関数の逆関数の例があることに注意してくださいここでは、関数の逆関数セクションにあります。
Here’s an example and graph:
|
Piecewise Function |
Graph |
|
\(\displaystyle f\left( x \right)=\left\{ \begin{align}2x+8\,\,\,\,\,&\text{ if }x\le -2\\{{x}^{2}}\,\,\,\,\,\,\,\text{ }\,&\text{ if }x>-2\end{align} \right.(これを表示するには、”if”の代わりに”for”を使用したり、”if”の代わりにカンマやセミコロンを使用するなど、他の方法があります。 ドメイン:\(\mathbb{R},\,\,\,\text{や}\,\,\left({-\infty,\infty}\right)\) 範囲: mathbb mathbb{R}、\、\、\、\テキスト{または}\、\、\左({-\inftyの、\inftyの}\右)\) |
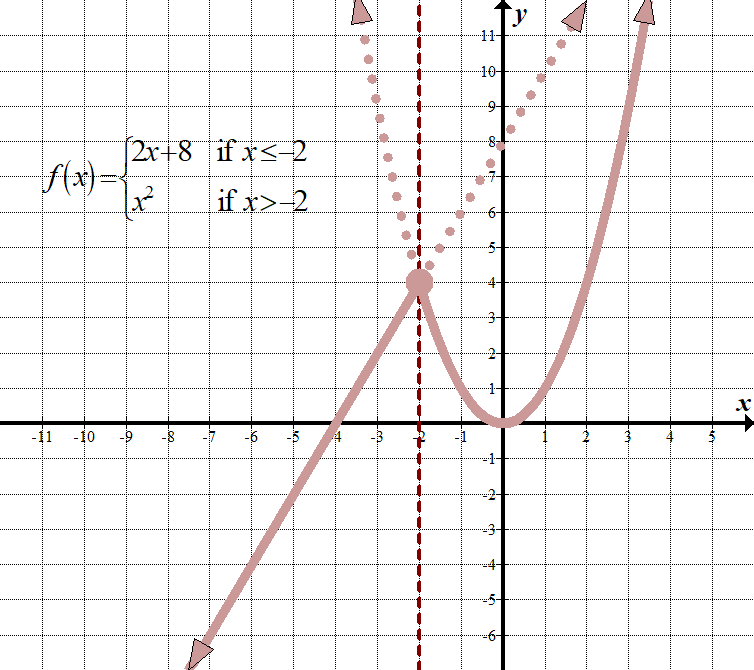 |
これは何を意味するのですかすべての\(X\)が-2以下である場合、グラフ上の唯一の関数であるかのように、線\(2x+8\)をグラフ化する必要があります。 -2より大きいすべての\(x\)値に対して、グラフ上の唯一の関数であるかのように、\({{x}.{2}}\)をグラフ化する必要があります。 それから私達は私達が必要としない部品を”取り払わなければならない”。 我々はまだ両方のグラフの基準点として原点を使用することを忘れないでください!垂直線\(x=-2\)が2つのグラフの間の「境界」線としてどのように機能するかを見てください。
点\((-2,4)\)には閉じた円があることに注意してください。
技術的には、その関数は等号以下であるため、\(2x+8\)関数にのみ属している必要がありますが、点は\({{x}.{2}}\)グラフ上にもあるため、両方の関数に表示されるかのように閉じた円を使用することができます。 そんなに悪くないでしょ?
区分的関数の評価
場合によっては、区分的関数が与えられ、それらを評価するように求められることがあります。
区分的関数の評価
; つまり、\(x\)の値が与えられたときに\(y\)の値を見つけます。 (グラフを使用せずに)\(x=-6\)と\(x=4\)に対してこれを行いましょう。 ここで再び関数である:
\(displaystyle f\left(x\right)=\left\{\begin{align}2x}\end{align}ここでは、関数は次のように定義されています。+8\,\,\,\,\,&\text{if}x\le-2\\{{x”>\text{if}x\le-2\\{x”>\text{if}}^{2}}\,\,\,\,\,\,\,\テキスト{}\、&\テキスト{もし}x>-2端\右{整列}。最初に右の条件を最初に見て、\(x\)がどこにあるかを確認したいと思います。\(x\)がどこにあるかを確認します。\(x\)がどこにあるかを確認します。\(x\)がどこにあるかを確認したいと思います。\(x\)がどこにあるかを確認したいと思います。\(x\)がどこにあるかを確認したいと思います。\(x\)がどこにあるかを確認したいと思います。\(x\)がどこにあるかを確認したいと思います。\(x\)が \(X=-6\)のとき、それは-2より小さいことがわかっているので、\(x\)を\(2x+8\)にのみ接続します。 \(f(x)\)または\(y\)は、\(f(x)\)である\((2)(-6)+8=-4\). 私たちは\(\boldsymbol{{x}2{2}}\)も気にしません! それは簡単です。 また、上記のグラフを使用して、これを正しく行ったこともわかります。 P>
今度は\(x=4\)を試してみてください。 最初に右を見て、\(x\)が-2より大きいことがわかりますので、\({{x}.{2}}\)にプラグインします。 (今回は\(2x+8\)を無視することができます。\(f(x)\)または\(y\)は、\(f(x)\)または\(f(x)\)です。\({{4}^{2}}=16\).
区分的関数のグラフ化
区分的関数をグラフ化するように求められるでしょう。 時には、グラフには非連続または不連続な関数が含まれていることがあり、グラフを描画するときにグラフの中央に鉛筆をピックアップする必要があ). 連続関数は、あなたが左から右にそれらを描画した場合、あなたの鉛筆をピックアップする必要はありませんことを意味します。そして、グラフは垂直線テストに合格した場合にのみ真の関数であることを覚えておいてください。
これらの区分的関数を描き、それらが連続的であるか非連続的であるかを判断しましょう。
これらの区分的関数が連続的であるか非連続的であ 各関数を唯一のものであるかのように描画し、必要のない部分を「消去」する方法に注意してください。 我々は代数関数のセクションでここでやったように我々はまた、ドメインと範囲を取得します。
| Piecewise Function | Graph |
|
\(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}-2x+8\,\,\,\,\,\,\text{if }x\le 4\\\frac{1}{2}x-2\,\,\,\,\,\,\,\,\,\text{if }x>4\end{array} \right.\) Continuous Domain: \(\mathbb{R},\,\,\,\text{or}\,\,\left( {-\infty ,\infty } \right)\) Range: \(\left( {0,\infty } \right)\) |
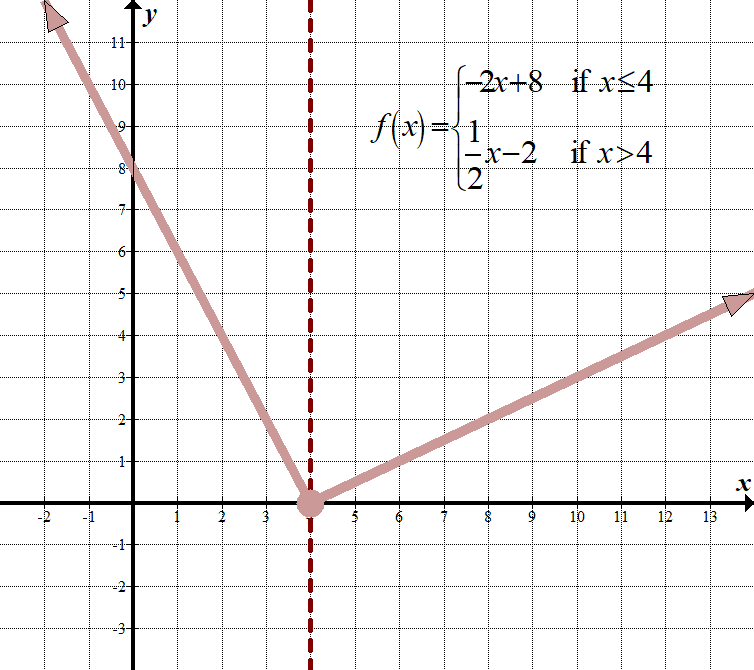 |
|
\(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}x+4\,\,\,\,\,\,\,\,\,\text{if }x<1\\2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{if 1}\le x<4\\x-5\,\,\,\,\,\,\,\,\,\text{if }x\ge 4\end{array} \right.\) Non-Continuous Domain: \(\mathbb{R},\,\,\,\text{or}\,\,\left( {-\infty ,\infty } \right)\) Range: \(\mathbb{R},\,\,\,\text{or}\,\,\left( {-\infty ,\infty } \right)\) |
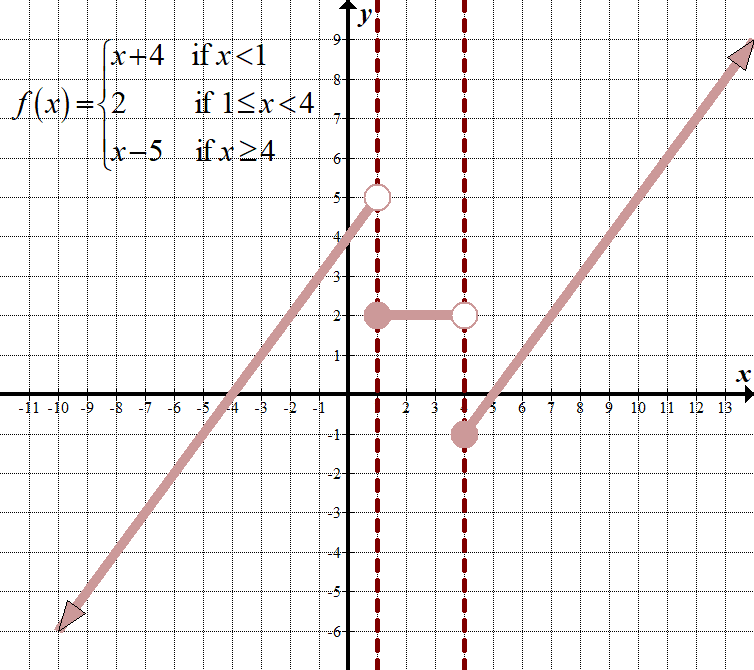 |
We can actually put piecewise functions in the graphing calculator:
| Piecewise Function Screens | Steps and Notes |
| Enter the piecewise function on three lines:ここでグラフです:
+4\,\,\,\,\,\,\,\,\,\text{if}x<1\\2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{if1}\le x<4\-5+x\,\,\,\,\,\テキスト{もし}x\ge4\端{アレイ}\右。計算機では、各区間の関数をその区間の「テスト不等式」で割ることによって、3行に関数を入力することができます(そして括弧を見てください!).たとえば、\((x+4)\)は\(x<1\)のときに\((x+4)/(1)\)になります。\(x<1\)の場合、計算機は1を返します。\(x<1\)の場合、\((x+4)\)は\((x+4)/(1)\)になります。 \(X\ge1\)のとき、0で除算しているので、何も描画されません。 ここでは、電卓に入れることができるものです:\begin{array}{l}{{Y}_{1}}=\left({x+4}\right)|\left({x<1}\right)|\left({x\ge1\text{and}x<1}\right)|\left({x\ge1\text{and}x<1}\right)|\left({x\ge1\text{and}x<1}\right)|\left({x\ge1\text{and}x<1}\right)|\left({X\ge1\text{and}x<1}\right)ff\{{y}_{3}}=\left({-5+X}\right)|\left({x\ge4}\right)\end{array}\) (これを1行に入力するには、除算の代わりに条件を乗算し、3つの関数/間隔のそれぞれの間にプラス記号を使: displaystyle X=\左({X+4}\右)\左({x<1}\右)+\左(2\右)\左({x\ge1\テキスト{と}x<4}\右)+\左({-5+x}\右)\左({x\ge4}\右)\左({x\ge4}\右)\左({X\ge4}\右)\左({X\ge4}\右)\左({X+4}\右)\左({x+4}\右)\左({x+4}\右)\左({x+4}\右)\左({x+4}\右)\左({x+4}\右)\左({X+4}\右)\左({X+4}\右)\左({X+4}\右)\)。) 三つの行を使用するためのキーストロークは次のとおりです。 2番目の数学(テスト)を使用して、\(\le\)、\(\ge\)などの画面に到達することに注意してください。 たとえば、2番目の数学6は\(\le\)を取得します。 {{Y}_{2}}\)の”and”には、2番目の数学(TEST)を使用し、論理に右、次に1を使用します。
|
区分的関数が連続または非連続であるかどうかを伝える方法
区分的グラフが連続または非連続であるかどうかを伝えるためには、境界点を見て、\(y\)点がそれぞれ同じであるかどうかを確認してください。 (もし\(y\)が異なっていたら、グラフに「ジャンプ」があるでしょう!)
上記で使用した関数でこれを試してみましょう:
| Piecewise Function | Check Boundary Points | |
| \(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}-2x+8\,\,\,\,\,\,\,\text{if }x\le 4\\\frac{1}{2}x-2\,\,\,\,\,\,\,\,\,\,\text{if }x>4\end{array} \right.\) | Let’s check \(x=4\) in both parts of the function, since 4 is the “boundary point”:
\(\開始{アレイ}{l}-2(4)+8=0\\\,\,\,\frac{1}{2}(4)-2=0\\(0=0\)なので、この区分的関数は連続的です。array\左(x\右)=\左\{\開始{アレイ}{l}x\開始{アレイ}{l}x\開始{アレイ}{l}x\開始{アレイ}{l}x\開始{アレイ}{l}x\開始{アレイ}{l}x\開始{アレイ}{l}x\開始{アレイ}{l}x\開始{アレイ}{l}x\開始{アレイ}{l}x\開始{アレイ}{l}x\開始{アレイ}{l}x\開始{アレイ}{+4\,\,\,\,\,\,\,\,\,\,\,\,\,\text{if}x<1\\2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{if1}\le x<4\-5+x\,\,\,\,\,\,\,\,\,\テキスト{もし}x\ge4\端{アレイ}\右。\) |
関数の最初の2つの部分を確認してみましょう。 注2番目の部分では、\(y\)は常に2です:
\(\開始{アレイ}{l}1+4=5\\\,\,\,\,\,\,\,\,\,2=2\\(5\ne2\)なので、ここで停止することができ、この区分的関数は非連続であることに注意してください。 \(Y\)が等しい場合は、\(x=4\)の次の境界点を確認するために1つ移動する必要があります。 |
区分関数グラフから方程式を得る
グラフが与えられた区分関数を書くように求められることがあ 区分的関数が何であるかを知ったので、それほど悪くはありません!
線形グラフから方程式を取得する方法を確認するには、線の方程式を取得するを参照し、二次方程式から点またはグラフから二次方程式を求ここにグラフがあり、区分的方程式を導出する方法についての説明があります。
:
| Piecewise Function Graph | Procedure to get Function |
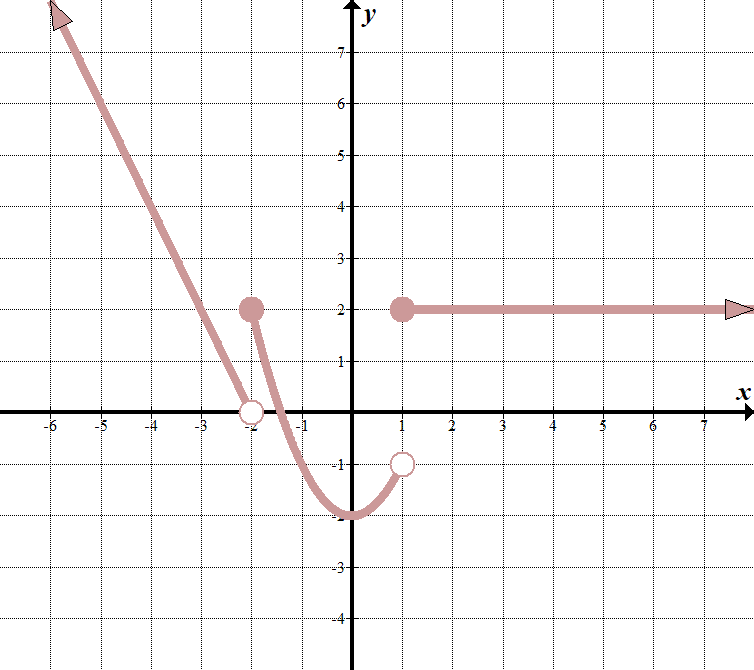 |
We see that our “boundary lines” are at \(x=-2\) and \(x=1\). We know that our function will look something like this (notice open and closed endpoints):f f\左(x\右)=\左\{\開始{アレイ}{l}\テキストを開始します。}\left(\begin{array}{l}\right)=\left(\begin{array}{l}\right)=\left(\begin{array}{l}\right)=\left(\begin{array}{l}\right)=0{ }……\,\,\,\,\,\,\,\,\テキスト{if}x<-2\\\テキスト{ }……\,\,\,\,\,\,\,\,\テキスト{if}-\テキスト{2}\ルx<1\\\テキスト{ }……\,\,\,\,\,\,\,\,\テキスト{もし}x\ge1\端{アレイ}\右。左の行に2つの点\((-2,0)\)と\((-3,2)\)を選択して、方程式\(y=-2x-4\)を得ることができます。中間の関数は\(y={{x}})です。
}^{2}}-2\), そして、一番右の関数はちょうど水平線\(y=2\)です。 したがって、区分的関数は次のようになります。 :array f\左(x\右)=\左\{\開始{アレイ}{l}-2x}\左\{\開始{アレイ}{l}-2x}\左\{\開始{アレイ}{l}-2x}\左\{\開始{アレイ}{l}-2x}\右\{アレイ}{l}-2x}\左\{アレイ}{l}-2x\左\{アレイ}{l}–4\,\,\,\,\,\,\,\テキスト{if}x<-2\\\テキスト{}{{x}^{2}}-2\,\,\,\,\,\,\,\,\,\,\テキスト{if}-\テキスト{2}\ルx<1\\\テキスト{ 2}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\テキスト{もし}x\ge1\端{アレイ}\右。私たちの”境界線”が\(x=5\)にあることがわかります。 行は\((5,4)\)で出会うので、\(\le\)または\(\ge\)記号をどこに置くかは問題ではありません; 私たちはそれを両方の場所に置くことができない、またはそれは機能ではないでしょう。 私たちはこれまで持っています: \(displaystyle f\left(x\right)=\left\{\begin{array}{l}\text}\end{array}{l}\text{配列}{l}\text{配列}{l}\text{配列}{l}\text{配列}{l}\text{配列}{l}\text{{ }……\,\,\,\,\,\,\,\,\,\テキスト{if}x<5\\\テキスト{ }……\,\,\,\,\,\,\,\,\,\テキスト{もし}x\ge5\端{アレイ}\右。繰り返しますが、各行を別々に見て、それらの方程式を決定する必要があります。 これらを得るために各行から2点を取るか、斜面と\(y\)-切片から導出することができます。:array\左(x\右)=\左\{\開始{アレイ}{l}\frac{6}{5}x\開始{アレイ}{l}\frac{6}{5}x\開始{アレイ}{l}\frac{6}{5}x\開始{アレイ}{l}\frac{6}{5}x\開始{アレイ}{l}\frac{6}{5}x\開始{アレイ}{l}\frac{6}{5}x\開始{アレイ}{-2\,\,\,\,\,\,\,\テキスト{if}x<5\\\frac{2}{5}x+2\,\,\,\,\,\,\,\テキスト{もし}x\ge5\端{アレイ}\右。 |
区分的関数としての絶対値
絶対値関数を区分的関数として書くことがで このトピックに進む前に、絶対値方程式と不等式を解くことを確認することをお勧めします。関数\(f\left(x\right)=\left|x\right|\)があるとしましょう。 私たちが以前に学んだことから、\(x\)が正のとき、絶対値を取っているので、それはまだ\(x\)になることを知っています。 しかし、\(x\)が負のとき、絶対値を取るとき、絶対値は正でなければならないので、反対の値を取らなければなりません(それを否定します)。 理にかなってる? したがって、たとえば、\(|5|\)があった場合、絶対符号の内側にあるものは正であるため、絶対符号の内側にあるものを取るだけです。 しかし、\(|-5|\)の場合、絶対値の内側にあるものの反対(負)を取って\(\displaystyle\)にする必要があります5\,\,\,(-\,-5=5)\).これは、この絶対値関数を区分的関数として書くことができることを意味します。
これは、この絶対値関数を区分的関数として書くことがで 絶対値の内側にあるものを0に設定することで、「転換点」または「境界点」を得ることができることに注意してください。 次に、その区間の関数の符号(絶対値なし)に応じて、元の関数を使用するか、関数を無効にします。たとえば、write left|x\right|\text{}=\left\{\begin{array}{l}x\}xと書くことができます。\,\,\,\,\,\,\,\,\,\テキスト{もし}x\ge0\-x\,\,\,\,\,\テキスト{if}x<0端\{アレイ}右。\). また、関数が境界点で連続している場合(「ジャンプ」がない場合)、それらを繰り返さない限り、「以下」(または「以上」)記号をどこに置くかは問題ではありません。 理論的には、同じ\(x\)に対して\(y\)の2つの値を持つことができないか、関数を持たないため、それらを繰り返すことはできません。
Here are more examples, with explanations. (You might want to review Quadratic Inequalities for the second example below):
| Absolute Value Function | Method to get Piecewise Function | ||||||||
| \(g\left( x \right)=\left| {2x+3} \right|\) | Let’s first find the “boundary line”. これを行うには、絶対値の内側にあるものを0に設定し、\(\boldsymbol{x}\)を解いてください。frac x\ge-\frac{3}{2}pとsolve x\ge-\frac{3}{2}pは、solve x\ge-\frac{3}{2}.とfrac x\ge-\frac{3}{2}.を意味します。 \(2x+3\)が正のとき、それを「そのまま」取るだけですが、負の場合は全体を否定する必要があります。
したがって、区分的関数は次のようになります。 :array left|{2x+3}\right|=\left\{\begin{array}{l}2x\right}\left\{\begin{array}{l}2x\right}\right\}divとなります。+3\,\,\,\,\,\,\,\,\,\テキスト{もし}x\ge-\frac{3}{2}\テキスト{}\-2x-3\,\,\,\,\,\テキスト{if}x<-\frac{3}{2}端\{アレイ}右。p> それを試してみてください-それは動作します!ここで、\(f\left(x\right)=\left|{{{x}-{2}}-4}\right|\) |
\(f\left(x\right)=\left|{{{x}-{2}}-4}\right|\) | iv id=”70f6f1258 {{x}-{2}}-4\ge0\)のとき、\(x\le-2\)または\(x\ge2\)が得られます(いくつかの数字を試してみてください!). {{X}.{2}}-4\)が正のとき、それを「そのまま」取るだけですが、負の場合は否定する必要があります。piec left|{{{x}-{2}}-4}\right|=\left\{\begin{array}{l}{{x}}-4\right|=\left\{\begin{array}{l}{{x}}-4\right|=\left\{\begin{array}{l}{{x}}-4\right|=\left\{\begin{array}{l}{x}}-4\right|=\left\{\begin{array}{l}{x}}-4\right|=\left\{\begin{array}{l}{x}}-4\right|=\}^{2}}-4\,\,\,\,\,\テキスト{もし}x\ル-2\4-{{x}^{2}}\,\,\,\,\,\テキスト{if}-2<x<2\\{{x}^{2}}-4\,\,\,\,\,\テキスト{もし}x\ge2\テキスト{}端\{アレイ}\右。{{{x}-{2}}-4}\right|=\left\{\begin{array}{l}{{x}}\right\}orは、array l lがl l arrayに収束することを示しています。}^{2}}-4\,\,\,\,\,\,\テキスト{もし}x\ル-2\テキスト{}\、\、\テキスト{または}\、\、\テキスト{}x\ge2\4-{{x}}\、\、\テキスト{}\、\、\テキスト{}\、\、\テキスト{}\、\、\テキスト{}\、\、\テキスト{}\、}^{2}}\,\,\,\,\,\,\,\テキスト{場合}-2<x<2端{アレイ}右。繰り返しますが(関数は連続しているので)、\(\le\)と\(\ge\)がどこにあるかは問題ではありません(\(<>\)absolute f\left(x\right)=2x+\left|{x+2}\right|\) | 絶対値の内側と外側に\(x\)があるので、これは少しトリッキーです。 「境界線」では、絶対値の内側にあるもののみを使用します。\(x+2\ge0\)のとき、\(x\ge-2\)が得られます。 しかし、区分的関数の場合、絶対値の外側にある部分を含む関数全体を使用する必要があります。 したがって、区分的関数は次のようになります:array2x+\left|{x+2}\right|=\left\{\begin{array}{l}2x+x\right|=\left\{\begin{array}{l}2x+x\right|=\left\{\begin{array}{l}2x+x\right|=\left\{\begin{array}{l}2x+x\right|=\left\{\begin{array}{l}2x+x\right+2\,\,\,\,\,\テキスト{もし}x\ge-2\2x-x-2\,\,\,\,\,\テキスト{if}x<-2端\{アレイ}右。2x+\left|{x+2}\right|=\left\{\begin{array}{l}3x\right|=\left\{\begin{array}{l}3x\right|=\left\{\begin{array}{l}3x\right|=\left\{\begin{array}{l}3x\right|=\left\{\begin{array}{l}3x\right|=\left\{\begin{array}{l}3x\right|=\left\{\begin{array}{l}3x\right|=\left\{\begin{array}{l}3x\right|=\left\{\begin{array}{l}3x\right|=\left\{+2\,\,\,\,\,\,\,\テキスト{もし}x\ge-2\x-2\,\,\,\,\,\,\,\,\,\,\テキスト{if}x<-2端\{アレイ}右。\)
いくつかの値を試してみてください-2;彼らは動作するはずです!これは、2次関数があり、関数が正と負のどこにあるかを知る必要があるため、符号チャートで最もよく解決されます。 |
|||||
| \(g\left(x\right)=\left/{{{x}^{2}}-4x-5}\right/\) | これは、2次関数があり、関数が正と負のどこにあるかを知る必要があるため、符号チャートで解決するのが最善です。まず、絶対値関数内の二次関数を\(\left({x-5}\right)\left({x+1}\right)\)に因数分解します。 次に、符号チャートを使用して、因子が正と負の場所を確認し、因子が正の場所では関数を「そのまま」使用し、因子が負の場所では関数を否定することを覚:array left|{{{x}begin{2}}-4x-5}\right|=\left\{\begin{array}{l}{{x}begin{2}}-4x-5}\right|=\left\{\begin{array}{l}{{x}^{2}}-4x-5}\right|=\left\{\begin{array}{l}{{x}^{2}}-4x-5}\right|=\left\{\begin{array}{l}{{x}^{2}}-4x-5}\right|=\left\{\begin{-5\,\,\,\,\,\,\,\,\,\,\,\,\,\,\テキスト{if}x\le-1\,\,\,\,\{{{x}^{2}}-4x-5}\right}ge{2}ge{2}ge{2}ge{2}ge{2}ge{2}ge{2}x{2}x{2}x{2}x{2}x{2}x{2}x{2}x{2}x{2})\,\,\,\,\テキスト{場合}-1<x<5\テキスト{}端{アレイ}右。これは有理数です。\frac{{\left|{x+2}\right|}}{{x+2}}\) | これは有理数です。\frac{{\left|{x+2}\right|}}{{x+2}}\) | これは有理数です。分母に変数があるので、関数。\(x+2\ge0\)とすると、\(\displaystyle x\ge-2\)が得られます。 しかし、absolute frac{1}{2}=\frac{1}{2}=\frac{1}{2}=\frac{1}{2}=\frac{1}{2}=\frac{1}{2}=\frac{1}{2}=\frac{1}{2}=\frac{1}{2}=\frac{1}{2}=\frac{1}{2}=\frac{1}{2}=\frac{1}{2}=\frac{1}{2}=\frac{1}{2}=\frac{1}{2}=\frac{1}{2}=\frac{1}{2}=\frac{1}{2}=\frac{1}{2}=\frac{+2}}\,\,\,\,\,\,\,\,\,\テキスト{もし}x\ge-2\\frac{{-x-2}}{{x+2}}\,\,\,\,\,\,\テキスト{if}x<-2端\{アレイ}右。\). しかし、\(x\ne2\)(ドメイン制限:分母は0になる)ので、注意する必要があります。
したがって、区分的関数は次のようになります。 : frac frac{1}{2}=\frac{1}{2}=\frac{1}{2}=\frac{1}{2}=\frac{1}{2}=\frac{1}{2}=\frac{1}{2}=\frac{1}{2}=\frac{1}{2}=0l}1\,\,\,\,\,\,\,\,\,\,\text{if}x>-2\\-1\,\,\,\,\,\,\テキスト{if}x<-2端\{アレイ}右。\).また、絶対値グラフを取って区分的関数として記述するように求められることもあります。 |
絶対値グラフを取って区分的関数として記述するように求められることもあります:
| Absolute Value Graph | Method to get Piecewise Function |
 |
We see that our “boundary line” is at \(x=0\), so what’s inside the absolute value sign must be \(x\) or a factor of \(x\). (これは、絶対値関数で境界線を取得するために、絶対値の内側にあるものを0に設定し、\(x\)を解くためです)。 x>0\)とすると、線の方程式が\(y=2x-2\)であることがわかります。 \(X<0\)のとき、方程式は\(y=2x-2\)です。 これを区分的関数として書くことができます。
\(displaystyle f\left(x\right)=\left\{\begin{array}{l}2x}\end{array}{l}2x\end{array}{l}2x\end{array}{l}2x\end{array}{l}2x\end{array}{l}2x\end{array}{l}2x\end{-2\,\,\,\,\,\,\,\0\-2x-2\、\、\、\テキスト{もし}x\ル0端\{アレイ}\右。これは、変換された絶対値関数として書くこともできます:\(y=2\left|x\right|-2\)または\(y=\left|{2x}\right|-2\)(2は正であるため、\(\left|{\,\,}\right|\)の内側または外側にあります。 (これは、\(\left|{\,\,}\right|\)の中にあるものが\(>0\)であるとき、通常の関数\(y=2x-2\)を使用し、内部にあるものが\(<0\)のとき、絶対値部分を否定して\(y=-\left({2x}\right)-2\))。私たちの「境界線」は\(x=2\)と\(x=-2\)にあるので、絶対値記号の内側にあるものは\(x-2\)の因数を持たなければなりません。\(x-2\)と\(x=-2\)の因数を持たなけそして\(x+2\)。 p>\(x<-2\)または\(x>2\)の場合、グラフはグラフの通常の部分のように見えることがわかります\(y={{x}^{2}}-4\). (私は要因を知り、良い推測をすることによってこれを理解しました!(-2<x<2\)の場合、方程式は反転されるか、または否定されます(\(x\)軸上で反転されます)。 これを区分的関数として書くことができます。 \left(\displaystyle f\left(x\right)=\left\{\begin{array}{l}{{x}}}}}}}}}}}}}}}}}^{2}}-4\,\,\,\,\,\,\,\,\,\テキスト{if}x<-2\テキスト{または}x>2\-{{x}^{2}}\テキスト{+ 4}\,\,\,\,\,\,\テキスト{もし}-2\ルx\ル2\端{アレイ}\右。これは、すべての\(y\)値が正であるため、その周りに絶対値を持つ変換された2次関数\(y={{x}.{2}}-4\)が始まったことがわかります。\(y=\left|{{{x}/{2}}-4}\right|\)。私たちの”境界線”は\(x=-2\)にあるので、絶対値記号の内側にあるものは\(x+2\)でなければなりません。\(x=-2\)でなければなりません。\(x=-2\)でなければなりません。\(x=-2\)でなければなりません。\(x=-2\)でなければなりません。\(x=-2\)でなければなりません。\(x=-2\)でなければなりません。\(x=-2\)でなければなりません。\(x=-2\)でなければなりません。\(x=-2\)でなければなりません。\(x=-2\)でなければなりません。\(x=-2\)でなければなりません。\(x=-2\)でなければなりません。\(x=-2\)でなければなりません。 x>-2\)とすると、線の方程式が\(y=-x-1\)であることがわかります。 \(X<-2\)の場合、行は\(y=x+3\)です。 これを区分的関数として書くことができます。 \(displaystyle f\left(x\right)=\left\{\begin{array}{l}-x}-\begin{array}{l}-\frac{1}{2}-\frac{1}{2}-\frac{1}{2}-\frac{1}{2}-\frac{1}{2}-\frac{1}{2}–1\,\,\,\,\,\,\テキスト{if}x>-2\\x+3\,\,\,\,\,\,\,\,\,\,\テキスト{もし}x\ル-2\端{アレイ}\右。これを変換された絶対値関数として書く方が簡単です。 親の絶対値関数が垂直方向に反転し、左2に移動し、上1に移動していることがわかります。 私たちの絶対値方程式は\(y=-\left|{x+2}\right)isです。|\,\,+\,\,1\). これは、上記の区分的関数と同じです。 それを試してみてください-それは動作します! |
区分的関数の変換
区分的関数の変換をしましょう。 ここでは、親関数とその変換について、親グラフと変換のセクションで学びました。 区分的変換を試みる前に、まずこのセクションを読むことをお勧めします。
次の区分的関数を\(x\)軸の周りに反転させ、垂直に2単位、右に1単位、上に3単位引き伸ばして変換しましょう。
次の区分的関数を\(x\)軸の周りに反転させ、垂直に2単位、右に1単位、上に3単位引き伸ばして変換します。ここで、\(-2f\left(x-1\right)+3\)を描画します。
\(\displaystyle f\left(x\right)=\left\{\begin{align}x+4\,\,\,\,\,\,\,\,&\text{if}x<\text{if}x<&\text{if1}\le x<4\\x-5\,\,\,\,\,\,\,\,&\text{if}x\ge4\end{align}\right。\)
変換のためにtチャートを埋めるときに、「境界」ポイントを使用するようにしましょう。 括弧内の変換は\(x\)に行われ(反対の数学を行う)、外側は\(y\)に行われることに注意してください。 下の表に示すように、tチャートを作成するには、「境界線」のそれぞれに2つの点を含むキーポイントを使用できます。
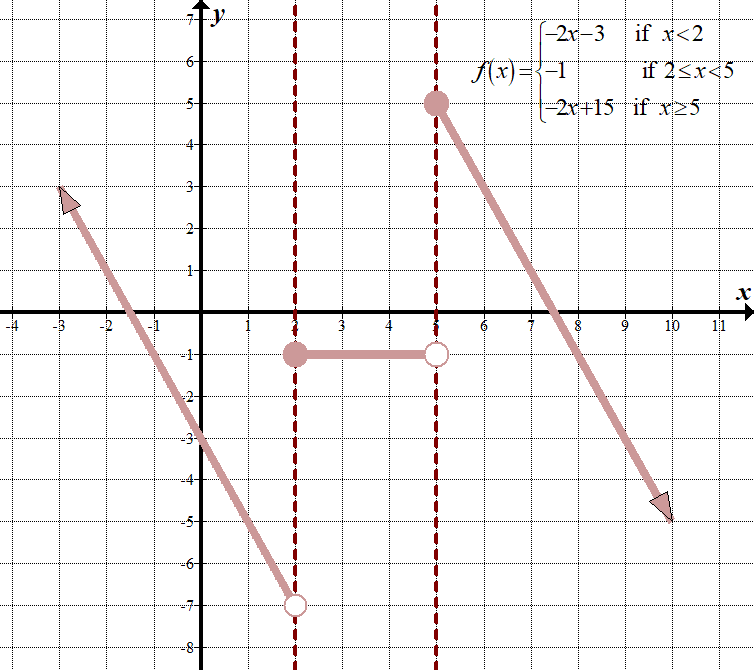
この変換は複雑であるため、3つの”pieces”を変換し、境界点がある”\(x\)”を変換することによって新しい区分的関数を考え出すことができます(1を加算するか、右1に行く)。”\(x\)”に対して反対の数学を行うので。 各区間で新しい関数を取得するには、元の方程式で”\(x-1\)”を”\(x\)”に置き換え、-2を掛けてから3を加算するだけです。 たとえば、\(\displaystyle-2f\left({x-1}\right)+3=-2\left+3=-2\left({x+3}\right)+3=-2x-3\)です。array left({x-1}\right)+3=\left\{\begin{array}{l}-2\left({\left({x-1}\right)+4}\right)+3=-2x\left({x-1}\right)+3=-2x\left({x-1}\right)+3=-2x\left({x-1}\right)+3=-2x\left({x-1}\right)+3=-2x\left({x-1}\right)+3=-2x\left({x-1}\right)+3=-2x\left({x-1}\right)+3=-2x\left(-3,\,\,\,\,\テキスト{if}x-1<1\、\、\、\left({x<2}\right)\-2\left(2\right)\-2\left(2\right)\-2\left(2\right)\-2\left(2\right)\-2\left(2\right)\-2\left(2\right)\-2\left(2\right)\-2\left(2\right)\-2\right)+3=-1,\,\,\,\,\テキスト{もし}\、\テキスト{2}\ルx<5\-2\左({\左({x-1}\右)-5}\右)+3=-2x+15,\,\,\,\,\テキスト{もし}x\ge5\端{アレイ}\右。\)
tチャートを含む”前”と”後”のグラフは次のとおりです:
| Piecewise Parent Function | T-chart | Transformation of Function | ||||||||||||||||||||||||||||||||||||||||
| \(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}x+4\,\,\,\,\,\,\,\,\text{if }x<1\\2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{if 1 }\le x<4\\x-5\,\,\,\,\,\,\,\,\text{if }x\ge 4\end{array} \right.\)
|
|
\(\displaystyle -2f\left( {x-1} \right)+3=\left\{ \begin{array}{l}-2x-3\,\,\,\,\,\,\,\,\,\text{if }x<2\\-1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{if 2}\le x<5\\-2x+15\,\,\,\,\,\,\text{if }x\ge 5\end{array} \right.\)
|
||||||||||||||||||||||||||||||||||||||||
Piecewise Function Word Problems
 Problem:あなたの好きな犬のグルーマーは、あなたの犬の体重に応じて料金を請求します。
Problem:あなたの好きな犬のグルーマーは、あなたの犬の体重に応じて料金を請求します。
あなたの犬が15ポンド以下の場合、groomerは$35を請求します。 あなたの犬が15と40ポンドの間にある場合、彼女はcharges40を請求します。 あなたの犬が40ポンドにあれば、彼女は各ポンドのための付加的な$2とadditional40を、満たす。
(a)あなたの犬のグルーマーが何を充電するかを説明する区分的関数を記述します。p>
(b)関数をグラフ化します。p>
(c)あなたのかわいい犬の重さが60ポンドの場合、グルーマーは何を請求しますか?
解決策
解決策:
(a)”境界点”は価格が変化する重みであるため、15と40であることがわかります。 私たちは2つの境界点を持っているので、区分的関数には3つの方程式があります。 犬は0ポンド以上の重量を量る必要があるので、我々は、0で開始する必要があります:array f\左(x\右)=\左\{\開始{アレイ}{l}\テキストを}\左\{\開始{アレイ}{l}\テキストを}\左\{\開始{アレイ}{l}\テキストを}\左\{\開始{アレイ}{l}\テキストを}\左\{\開始{アレイ}{l}\テキストを}\左\{\開始{アレイ}{l}\テキストを}\{ }……\,\,\,\,\,\,\,\,\,\テキスト{if}0<x\le15\\\テキスト{ }……\,\,\,\,\,\,\,\,\,\テキスト{if}15<x\le40\\\テキスト{ }……\,\,\,\,\,\,\,\,\,\テキスト{if}x>40端{アレイ}右。\)
私たちは、価格の三つの範囲のための”質問”(犬の重量を量るどのくらい)に”答え”(グルーミングのコスト)を探しています。 最初の2つは定額料金です(それぞれ$35と4 40)。 最後の方程式は少しトリッキーです; groomerはcharges40プラスeach2以上の各ポンドのために40を充電します。 実際の数字を試してみましょう:あなたの犬の体重が60ポンドの場合、彼女はcharge40プラス$2回\(20(60-40)\)を請求します。 これを式に変換します:\(40+2(x-40)\)、これは\(2x–40\)に単純化されます(2が傾きである方法を参照してください)。).
区分的関数全体は次のようになります。
:array f\左(x\右)=\左\{\開始{アレイ}{l}\テキストを}\左\{\開始{アレイ}{l}\テキストを}\左\{\開始{アレイ}{l}\テキストを}\左\{\開始{アレイ}{l}\テキストを}\左\{\開始{アレイ}{l}\テキストを}\左\{\開始{アレイ}{l}\テキストを}\{ }35\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\テキスト{if}0<x\le15\\\テキスト{ }40\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\テキスト{if}15<x\le40\\テキスト{}40+2\left({x-40}\right)\,\,\,\,\,\,\テキスト{if}x>40端{アレイ}右。f f(x\右)=\左\{\開始{アレイ}{l}\テキストを}開始{アレイ}{l}\テキストを開始{アレイ}{l}\テキストを開始{アレイ}{l}\テキストを開始{アレイ}{l}\テキスト{ }35\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\テキスト{if}0<x\le15\\\テキスト{ }40\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\テキスト{if}15<x\le40\\\テキスト{}2x-40\,\,\,\,\,\,\,\テキスト{if}x> この区分的方程式は非連続であることに注意してください。
この区分的方程式は非連続であることに注意してください。 この区分的方程式は非連続であることに注意してください。 また、この問題の合理的なドメインは\(\left({0,200}\right]\)かもしれないことに注意してください(犬は200ポンド以上の重さではありません! 妥当な範囲は\(\left\cup\left\)である可能性があります。(c)あなたの犬の体重が60ポンドの場合、グラフまたは関数を使用して$80を支払わなければならないことを確認できます。 おっと! それは人間のヘアカット(少なくとも私のヘアカット)以上の費用がかかります!P>
この区分的方程式は非連続であることに注意してください。 また、この問題の合理的なドメインは\(\left({0,200}\right]\)かもしれないことに注意してください(犬は200ポンド以上の重さではありません! 妥当な範囲は\(\left\cup\left\)である可能性があります。(c)あなたの犬の体重が60ポンドの場合、グラフまたは関数を使用して$80を支払わなければならないことを確認できます。 おっと! それは人間のヘアカット(少なくとも私のヘアカット)以上の費用がかかります!P>
あなたは彼女が募金活動として数学のtシャツを愛して販売する予定です。
あなたは彼女が数学のtシャツを愛して販売する予定です。
卸し売りtシャツの会社はfirst10最初の75のワイシャツのためのワイシャツを満たす。 最初の75シャツの後、あなたは150シャツまで購入し、同社はシャツあたり$7.50にその価格を下げます。 あなたは150シャツを購入した後、価格はシャツあたり$5に減少します。 この状況をモデル化する関数を記述します。
解決策:
「境界点」は、価格が変わるところで購入されたtシャツの数であるため、75と150であることがわかります。
解決策:
私たちは、「境界点」が75と150であることを確認してください。 私たちは2つの境界点を持っているので、区分的関数には3つの方程式があります。 少なくとも1つのシャツが購入されていると仮定しているので、\(x\ge1\)から始めます。 この問題では、購入したtシャツの数(\(x\))、またはドメインは整数でなければなりませんが、この制限は問題の結果に影響を与えません。左\{\開始{アレイ}{l}\テキスト{}……\テキスト{もし}1\ルx\ル75\\テキスト{}……\テキスト{もし}75<x\ル150\\テキスト{}……\テキスト{もし}75<x\ル150\\テキスト{}…….\テキスト{もし}75<x\ル150\\テキスト{}…….\テキスト{もし}75<x\ル150\\テキスト{}…….\テキスト{もし}75<…\テキスト{場合}X>150端{アレイ}右。\)
私たちは、価格の三つの範囲のための”質問”(購入されているどのように多くの)への”回答”(tシャツの総コスト)を探しています。p>
最大75枚のシャツを含む場合、価格は$10なので、合計価格は\(10x\)になります。 75以上のシャツが、最大100シャツの場合、コストは$7.50ですが、最初の75tシャツはまだシャツあたり$10の費用がかかります。 2番目の関数には、最初の75枚のシャツに費やされた$750(75倍の$10)が含まれ、75枚以上のシャツの数の$7.50倍も含まれています。\((x-75)\)。 たとえば、80枚のシャツを購入した場合、\(\$10\times75=\$750\)、プラス\(\7 7.50\times\)を費やす必要があります5\,\) (80 – 75) 75番目のシャツの後のシャツのために。同様に、150以上のシャツについては、10ドルの価格を75枚のシャツ、7ドルまで支払うことになります。50のための価格76へ150シャツ(75より多くのシャツ),その後、shirts5以上買ったシャツの数のためのシャツあたり150. 私たちは支払うでしょう\(10(75)+7.50(75)+5(x-150)\)のための\(x\)シャツ. 数字に入れて、それを試してみてください!piec\左(x\右)=\左\{\開始{アレイ}{l}\テキスト{}10x\開始{アレイ}{l}\テキスト{}10x\開始{アレイ}{l}\テキスト{}10x\開始{アレイ}{l}\テキスト{}10x\開始{アレイ}{l}\テキスト{}10x\開始{アレイ}{l}\テキスト{}10x\開始{アレイ}{l}\テキスト{}10x\開始{アレイ}{l}\テキスト{}10x\開始{アレイ}{l}\テキスト{}10x\開始{アレイ}{l}\テキスト{}10x\開始{アレイ}{l}\テキスト{}10x\開始\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\テキスト{場合}1\ルx\ル75\\\テキスト{}7.5x\テキスト{}+\テキスト{ }187.5\,\,\,\,\,\テキスト{if7}5<x\le150\\\テキスト{}5x+562。5\,\,\,\,\,\,\,\,\,\,\テキスト{if}x>150端{アレイ}右。displaystyle f(x\右)=\左\{\開始{アレイ}{l}\テキスト{}10x\開始{アレイ}{l}\テキスト{}10x\開始{アレイ}{l}\テキスト{}10x\開始{アレイ}{l}\テキスト{}10x\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\テキスト{場合}1\ルx\ル75\\\テキスト{}7.5x\テキスト{}+\テキスト{ }187.5\,\,\,\,\,\テキスト{if7}5<x\le150\\\テキスト{}5x+562.5\,\,\,\,\,\,\,\,\,\,\,\テキスト{if}x>150端{アレイ}右。問題:
バスサービスは、最初の400マイルのために$50の費用がかかり、各追加の300マイル(またはその一部)は、運賃に1 10を追加します。
区分的関数を使用して、バスの運賃をマイル単位の距離で表します。これは実際には難しい問題ですが、最初に400である「境界点」について最初に考えてみましょう。 乗車が400マイルよりより少しのときそれはかなり簡単である;費用は$50である。
400マイルを超える場合は、最初の400マイルを減算し(ただし、最初の$50を含めることを忘れないでください)、残りのマイル数を300マイルで割ります(小数
トリッキーな部分は、次の300マイルの一部を”切り上げる”ときです。 “Ceiling”関数(\(\left\lceil{}\right\rceil\)で指定)を使うことができます;この関数は入力以上の最小の整数を与えます;例えば、3.5と4の両方の上限は4です。
したがって、これは私たちが持っているものです:displaystyle f\左(x\右)=\左\{\開始{アレイ}{l}\テキスト{}50\テキストを開始します。\begin{array}{l}\text{}50\text{}50\text{}50\text{}50\text{}50\text{}50\text{}50\text{}50\text{}50\text{}50\text{}50\text{}50\text{}{ }\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\テキスト{もし}0\ルx\ル400\\テキスト{}50+10\回\左\lceil{\frac{{x-400}}{{300}}} \右\rceil\テキスト{ }\,\,\,\,\,\,\テキスト{if}x>400端{アレイ}右。\)
それを試してみましょう! 1500マイルの乗車がある場合、コストは\(\displaystyle50+10\times\left\lceil{\frac{10000000000000}{\frac{10000000000000}})になります。{{1500-400}}{{300}}} \右\rceil\テキスト{}=50+10\回4=$90\)。
問題:
\(\boldsymbol{a}\)のどの値がこの区分的関数を連続的にするのでしょうか?array f\左(x\右)=\左\{\開始{アレイ}{l}3{{x}を}開始{アレイ}{l}3{{x}を}開始{アレイ}{l}3{{x}を}開始{アレイ}{l}3{{x}を}開始{アレイ}{l}3{{x}を}開始{アレイ}{l}3{{x}を}開始{アレイ}{l}3{{x}}^{2}}+4\,\,\,\,\,\テキスト{if}x<-2\\5x+\boldsymbol{a}\,\,\,\,\,\,\,\,\テキスト{もし}x\ge-2\端{アレイ}\右。解決策:
区分的関数が連続的であるためには、境界点(関数が変化する場所)で、2つの\(y\)値が同じでなければなりません。 両方の関数で-2をプラグインして、\(y\)が同じであることを確認できます
\(\begin{align}3{{x}^{2}}+4&=5x+a\3{{\left({-2}\right)}\right)={-2}\left({-2}\right)dd{-2}\left({-2}\right)+{-2}\left({-2}\right)+{-2}\left({-2}\right)+{-2}\left({-2}\right)+{-2}\left({-2}\right)+{-2}\right)begin)}^{2}}+4-10+a\a&=26\end{align}\)
\(a=26\)の場合、区分的関数は連続しています!
これらのルールを学び、練習、練習、練習!
より多くの練習:区分的関数を書くことを試みるために、以下のMathwayウィジェットを使用してください。 Submit(問題の右側にある青い矢印)をクリックし、絶対値を区分的に書き込むをクリックして答えを確認します。
自分の問題を入力するか、右上隅にある三つのドットをクリックして”例”をクリックしてトピックごとにドリルダウンすることもできます。
タップをクリックしてステップを表示するか、ここをクリックすると、Mathwayで無料トライアルに登録し、いつでも有料サブスクリプションにアップグ).
行列と行列を持つシステムを解くために–あなたは準備ができています!