角度と円についてのいくつかの興味深いこと。
内接角度
まず、定義:
内接角度:円の円周上に座っている点から作られた角度。
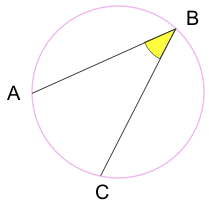
AとCは”終点”です
Bは”頂点点”です
ここで遊ぶ:
ポイント”B”を移動すると、角度はどうなりますか?
内接角定理
内接角a°は中心角2a°の半分です
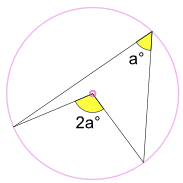
(中心定理の角度と呼ばれる)
と(端点を固定したまま)。..
。.. 角度a°は常に同じです、
それはエンドポイント間の同じ円弧上にあるに関係なく:
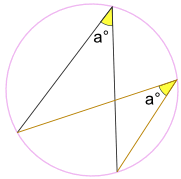
角度a°は同じです。
(同じアーク定理によってSubtended角度と呼ばれます)
例:角度POQのサイズは何ですか?
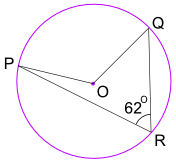
角度POQ=2×角度PRQ= 2 × 62° = 124°
例:角度CBXのサイズは何ですか?h3>
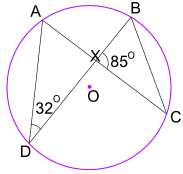
角度ADB=32°も角度ACBに等しくなります。
角度ACBも角度XCBに等しくなります。したがって、三角形BXCでは角度BXC=85°、角度XCB=32°を知っています。
三角形の角度を180°に加算して使用します。
:
半円の角度(タレスの定理)
円の直径に内接する角度は常に直角です:
(端点は円の直径の端であり、
頂点点は円周上の任意の場所にすることができます。 p>
なぜですか?
内接角90°は中心角180°の半分です
(上記の”中心定理での角度”を使用)
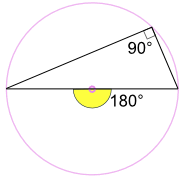
それが動作するもう一つの正当な理由
それが動作するもう一つの正当な理由
h3>
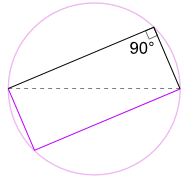
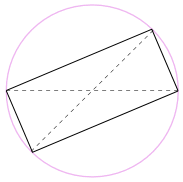
また、長方形を作るために180°の周りに形状を回転させる
すべての辺が平行で、両方の対角線が等しいため、長方形です。したがって、その内角はすべて直角(90°)です。
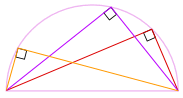
だから、私たちは行きます! その角度が円周上で
どこにあっても、それは常に90°です
例:角度BACのサイズは何ですか?
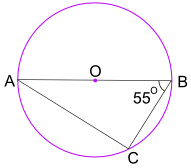
半円定理の角度は、角度ACB=90°
三角形の角度を180°に追加して角度BACを見つけることができます:
円の中心を見つける
私たちは、円の中心を見つけるために、このアイデアを使用することができます。
- 円の円周上の任意の場所から直角を描画し、二つの脚がヒット直径を描画します円
- もう一度それを行いますが、異なる直径
ここで、直径が交差するのは中心です!
環状四辺形
|
“環状”四辺形は、円の円周上のすべての頂点を持っています。 |
 |
|
周期的な四辺形の反対の角度は、円の円周上のすべての頂点を持っています。 |
|
|
周期的な四辺形の反対の角度は、円の円周上のすべての頂点を持っています。 |
|
|
周期的な四辺形の反対の角度は、円の円周上のすべての頂点を持っています。 |
|
|
180°:
|
 |
例:角度Wxyのサイズは何ですか?
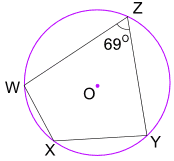
Opposite angles of a cyclic quadrilateral add to 180°

