• Purplemath
• MathHelp.com
• ダブルアングルId
• ハーフアングルId
• ハーフアングルId
• Sum Identities
• Product Identities

Purplemath

数学では、”恒等式”は常に真である方程式です。 これらは、”x=x”のように”自明に”真であるか、ピタゴラスの定理の直角三角形の”a2+b2=c2″のように有用である可能性があります。 そこ三角恒等式の負荷がありますが、以下は、あなたが見て使用する可能性が最も高いものです。

Basic & Pythagorean, Angle-Sum & -Difference, Double-Angle, Half-Angle, Sum, Product

Content Continues Below

MathHelp.com

Need a custom math course?
K12 | College | Test Prep

div>

アフィリエイト

“co-（何か）”trig比が常にいくつかの”非co”比の逆数であることに注意してください。 この事実を使用して、cosecantが正弦波で、secantが余弦波であることをまっすぐに保つのに役立ちます。

以下のもの（特に以下の3つのうちの最初のもの）は「ピタゴラス」恒等式と呼ばれています。

上記の三つのアイデンティティは、二乗と数1を含むことに注意してください。 角度がt、「反対」側がsin（t）=y、「隣接」側がcos（t）=x、斜辺が1の単位円を考えると、ピタゴラスとその関係がはっきりとわかります。

trig比の機能状態に関連する追加のアイデンティティがあります。

特に、正弦と正接は奇数関数であり、原点について対称であり、余弦は偶数関数であり、y軸について対称であることに注意してください。 引数の「マイナス」記号を外側に（正弦と正接の場合）取ることができるか、完全に（余弦の場合）排除できるという事実は、複雑な式を扱うときに役立ちます。Sin(α+β)=sin(α)cos(β)+cos(α)sin(β)

Sin(α-β)=sin(α)cos(β)-cos(α)sin(β)

Cos(α+β)=cos(α)cos(β)–sin(α)sin(β)

Cos(α–β)=sin(α)cos(β)–sin(α)sin(β)

Cos(α–β)=sin(α)cos(β)-sin(α)sin(β)

Cos(α-β)=sin(α)cos(β)-sin(α)sin(β)

sin(α-β)=sin(α-β)

cos(α-β)=sin(α-β)

sin(α-β)=sin(α-β)

sin(α-β)=sin(cos(α)cos(β)+Sin(α)Sin(β)

ちなみに、上記の恒等式では、角度はギリシャ文字で示されています。 A型の文字「α」は「α」と呼ばれ、「AL-fuh」と発音されます。 B型の文字”β”は”β”と呼ばれ、”BAY-tuh”と発音されます。

ダブルアングルId

ハーフアングルId

Sin(2x)=2sin(x)cos(x)=1–2sin2(x)=2cos2(x)-1

ハーフアングルId

div>

上記のアイデンティティは、各辺を二乗して再記述することができます。すべての角度測定値を2倍にします。 結果は次のとおりです:

Affiliate

Sum Identities

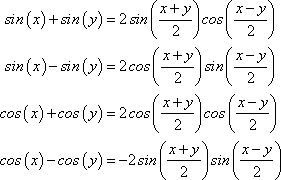
Product Identities

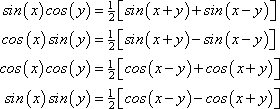
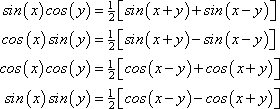
アフィリエイト

あなたは、他のtrig idを証明し、trig方程式を解くために、これらのidのすべてを使用するか、ほとん ただし、微積分学を研究する場合は、積分計算でそれらを多く使用するため、再記述された正弦と余弦の半角の恒等式に特に注意してください。