ケーニヒスベルクはプレガー川の町であり、18世紀にはドイツの町だったが、現在はロシアの町である。 町の中には二つの島があり、七つの橋で銀行に接続されています（下に示すように）。

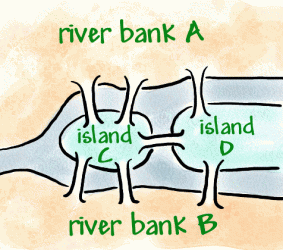
一度だけ各橋を渡る方法で町を歩くことを試みるのが伝統になりましたが、難しい問題であることが判明しました。 Leonhard Euler、スイスの数学者ロシアの皇后Catherine The Greatは、この問題について聞いた。1736年、オイラーは歩行が不可能であることを証明した。 これは、頂点（線が出会う点）と円弧（線）で構成されています。

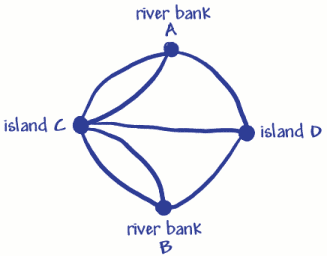
彼は二つの川岸とtwoislandsのための四つのドット（頂点）を使用しました。 これらはa、B、C、Dとマークされています。 あなたは3つの橋（アーク）が川岸Aに参加し、3が川岸Bに参加することがわかります。5つの橋（アーク）が島Cに参加し、3が島Dに参加します。 これは、すべての頂点が奇数の円弧を持つことを意味するので、それらはoddverticesと呼ばれます。 （偶数の頂点は偶数の円弧を持つ必要がありますそれに隣接しています）。
問題は、一度だけeachbridgeを横断する町の周りを移動することだったことを覚えておいてください。 オイラーのネットワーク上では、これは一度だけ各頂点をトレースし、すべての頂点を訪問することを意味した。 オイラーは、その頂点で旅行を開始または終了するために奇妙な頂点を持つことを働いたので、それを行うことができないことを証明しました。 （それについて考えてみてください）。開始点と終了点は1つしかないため、eacharcを一度だけトレースできるようにするには、奇数の頂点が2つしかない可能性があります。 ブリッジ問題には4つの奇数頂点があるため、実行することはできません！ 奇数の頂点がすべてない場合はどうなりますか？ このネットワークは追跡できますか？

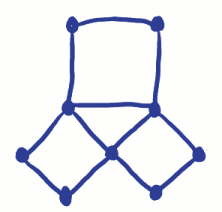
ネットワークの発明は、トポロジーと呼ばれる全く新しいタイプの幾何学を始めました。 トポロジーは現在、計画や鉄道網のマッピングなど、多くの方法で使用されています。 （ああ！ 列車は入って来なければならなかったそれ。…）