Alcune cose interessanti su angoli e cerchi.
- Angolo inscritto
- Teoremi dell’angolo inscritto
- Esempio: Qual è la dimensione dell’angolo POQ? (O è il centro del cerchio)
- Esempio: Qual è la dimensione dell’angolo CBX?
- Angolo in un Semicerchio (Teorema di Talete)
- un Altro Buon Motivo per cui Funziona
- Esempio: qual è la dimensione dell’angolo BAC?
- la Ricerca di un Centro del Cerchio
- Quadrilatero Ciclico
- Esempio: Qual è la dimensione dell’Angolo WXY?
Angolo inscritto
Prima di tutto, una definizione:
Angolo inscritto: un angolo fatto da punti seduti sulla circonferenza del cerchio.
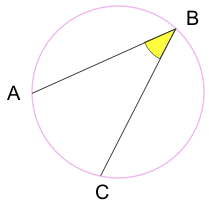
A e C sono “punti finali”
B è il “punto apice”
Gioca con esso qui:
Quando sposti il punto “B”, cosa succede all’angolo?
Teoremi dell’angolo inscritto
Un angolo inscritto a° è metà dell’angolo centrale 2a°
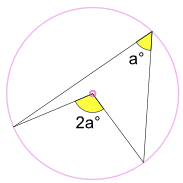
(chiamato Teorema dell’angolo al centro)
E (mantenendo fissi i punti finali) …
… l’angolo a° è sempre lo stesso,
non importa dove si trova sullo stesso arco tra i punti finali:
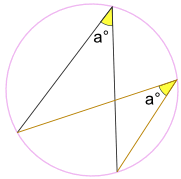
L’angolo a° è lo stesso.
(Chiamato gli angoli sottesi dallo stesso teorema dell’arco)
Esempio: Qual è la dimensione dell’angolo POQ? (O è il centro del cerchio)
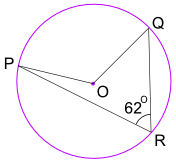
Angolo POQ = 2 × Angolo PRQ = 2 × 62° = 124°
Esempio: Qual è la dimensione dell’angolo CBX?
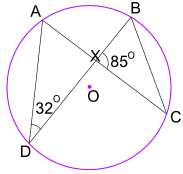
L’angolo ADB = 32° equivale anche all’angolo ACB.
E l’angolo ACB eguaglia anche l’angolo XCB.
Quindi nel triangolo BXC conosciamo l’angolo BXC = 85° e l’angolo XCB = 32 °
Ora usa gli angoli di un triangolo aggiungi a 180° :
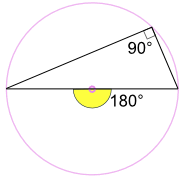
Angolo in un Semicerchio (Teorema di Talete)
Un angolo inscritto su un diametro del cerchio è sempre un angolo retto:
(fine i punti sono una delle estremità di un diametro del cerchio,
l’apice punto può essere qualsiasi punto della circonferenza.)
|
Perché? Perche: inscritto angolo di 90° è la metà dell’angolo al centro di 180° (Usando “l’Angolo al Centro Teorema” di cui sopra) |
 |
un Altro Buon Motivo per cui Funziona
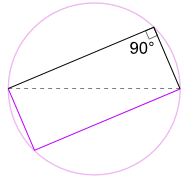
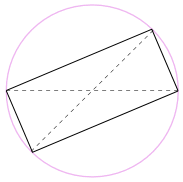
Si può anche ruotare la forma attorno a 180° per fare un rettangolo!
È un rettangolo, perché tutti i lati sono paralleli ed entrambe le diagonali sono uguali.
E quindi i suoi angoli interni sono tutti angoli retti (90°).
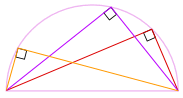
Quindi ci siamo! Non importa dove si trova quell’angolo
sulla circonferenza, è sempre 90 °
Esempio: qual è la dimensione dell’angolo BAC?
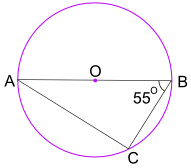
L’angolo nel teorema del semicerchio ci dice che l’angolo ACB = 90°
Ora usa gli angoli di un triangolo aggiungi a 180° per trovare l’angolo BAC:
la Ricerca di un Centro del Cerchio
E ‘ possibile utilizzare questa idea per trovare un centro del cerchio:
- disegnare un angolo retto da qualsiasi punto della circonferenza del cerchio, quindi disegnare il diametro dove le due gambe colpire il cerchio
- farlo di nuovo, ma per un diametro diverso
in Cui i diametri croce è il centro!
Quadrilatero Ciclico
|
“Ciclico” Quadrilatero ha ogni vertice sulla circonferenza del cerchio: |
 |
|
Un Quadrilatero Ciclico opposto angoli aggiungere a 180°:
|
 |
Esempio: Qual è la dimensione dell’Angolo WXY?
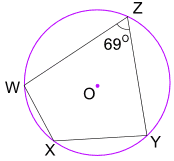
Opposite angles of a cyclic quadrilateral add to 180°

