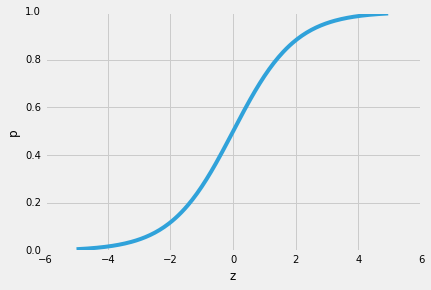
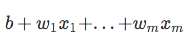Quindi, una delle belle proprietà della regressione logistica è che la funzione sigmoid emette le probabilità condizionali della previsione, le probabilità di classe. Come funziona?Iniziamo con il cosiddetto “odds ratio” p / (1-p), che descrive il rapporto tra la probabilità che si verifichi un certo evento positivo e la probabilità che non si verifichi – dove positivo si riferisce all’ “evento che vogliamo prevedere”, cioè p(y=1 | x).
(Si noti che la regressione logistica è un tipo speciale di funzione sigmoide, il sigmoide logistico; esistono altre funzioni sigmoidiche, ad esempio la tangente iperbolica).
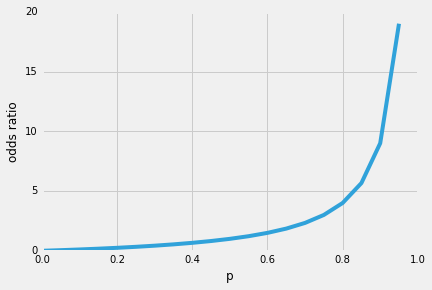
Quindi, più è probabile che si verifichi l’evento positivo, maggiore è il rapporto delle probabilità.Ora, se prendiamo il logaritmo naturale di questa possibilità’ di rapporto, il log-odds o logit funzione, si ottiene la seguente
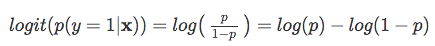
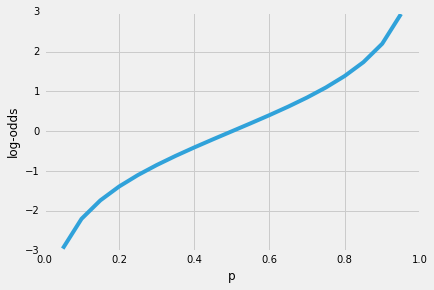
poi, usiamo questa trasformazione logaritmica per modellare la relazione tra variabili esplicative e la variabile target:
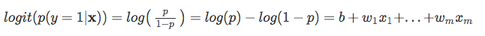
| Ora, tienilo a mente che non stiamo cercando di predire la parte destra dell’equazione di cui sopra, dal momento che *p(y=1 | x)* è quello che ci interessa veramente. So, let’s take the inverse of this logit function … et viola, we get the logistic sigmoid: |
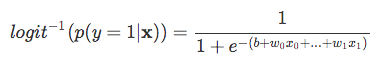
| which returns the class probabilities *p(y=1 | x)* from the inputs |