Konigsberg è una città sul fiume Preger, che nel xviii secoloera una città tedesca, ma ora è russa. All’interno della città ci sono dueisole fluviali che sono collegate alle rive con sette ponti(come mostrato di seguito).

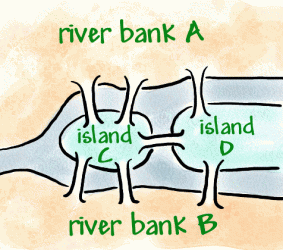
È diventata una tradizione provare a camminare per la città in un modo chesolo attraversato ogni ponte una volta, ma si è rivelato un difficileproblema. Leonhard Euler, un matematico svizzero al servizio dil’imperatrice russa Caterina la Grande, ha sentito parlare del problema.Nel 1736 Eulero dimostrò che la passeggiata non era possibile fare. Ha migliorato questo inventando una sorta di diagramma chiamato rete, cheè costituito da vertici (punti in cui le linee si incontrano) e archi(linee).

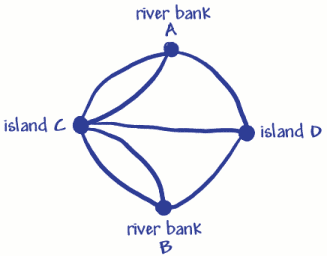
Ha usato quattro punti (vertici) per le due sponde del fiume e le due isole. Questi sono stati contrassegnati A, B e C, D. Le sette linee (archi) sono i sette ponti. Puoi vedere che 3 ponti (archi)si uniscono alla riva del fiume A e 3 si uniscono alla riva del fiume B. 5 ponti (archi)si uniscono all’isola C e 3 si uniscono all’isola D. Ciò significa che tutti i thevertices hanno un numero dispari di archi, quindi sono chiamati oddvertices. (Un vertice pari dovrebbe avere un numero pari di archi che si uniscono ad esso).
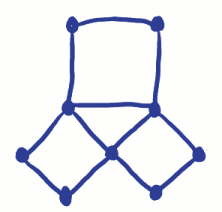
Ricordate che il problema era quello di viaggiare in città attraversando eachbridge solo una volta. Sulla rete di Eulero ciò significava tracciare su ciascunoarco solo una volta, visitando tutti i vertici. Eulero ha dimostrato che non poteva essere fatto perché ha capito che per avere un vertice dispari avresti dovuto iniziare o terminare il viaggio a quel vertice. (Pensaci).Dal momento che ci può essere solo un inizio e una fine, ci possono essere solo due vertici dispari se sarai in grado di tracciare su ciascun arc solo una volta. Poiché il problema del bridge ha 4 vertici dispari, non è possibile farlo! Cosa succede se non ci sono vertici dispari atutti? Questa rete può essere tracciata?

L’invenzione delle reti ha iniziato un nuovo tipo di geometria chiamatatopologia. La topologia è ora utilizzata in molti modi, anche per la pianificazionee la mappatura delle reti ferroviarie. (Ahhh! I treni dovevano entrarenon….)