Il piano delle coordinate
Obiettivi di apprendimento
· Tracciare coppie ordinate su un piano delle coordinate.
· Data una coppia ordinata, determinare il suo quadrante.
Introduzione
Il piano delle coordinate è stato sviluppato secoli fa e perfezionato dal matematico francese René Descartes. In suo onore, il sistema è talvolta chiamato il sistema di coordinate cartesiane. Il piano delle coordinate può essere utilizzato per tracciare punti e linee del grafico. Questo sistema ci consente di descrivere le relazioni algebriche in senso visivo e ci aiuta anche a creare e interpretare concetti algebrici.
Conoscere il piano delle coordinate
Probabilmente hai già usato un piano delle coordinate. Ad esempio, hai mai usato una sovrapposizione a griglia per mappare la posizione di un oggetto? (Questo è spesso fatto con mappe stradali, anche.)

Questa “mappa” utilizza una griglia orizzontale e verticale per trasmettere informazioni sulla posizione di un oggetto. Si noti che le lettere A-F sono elencate lungo la parte superiore e i numeri 1-6 sono elencati lungo il bordo sinistro. La posizione generale di qualsiasi elemento su questa mappa può essere trovata usando la lettera e il numero del suo quadrato della griglia. Ad esempio, è possibile trovare l’elemento che esiste al quadrato “4F” spostando il dito lungo l’orizzontale alla lettera F e poi verso il basso in modo da essere in linea con il 4. Troverete un disco blu è in questa posizione sulla mappa.
Il piano delle coordinate ha elementi simili alla griglia mostrata sopra. Consiste di un asse orizzontale e un asse verticale, linee numeriche che si intersecano ad angolo retto. (Sono perpendicolari l’uno all’altro.)
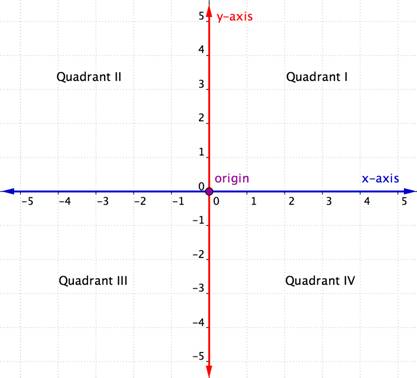
L’asse orizzontale nel piano delle coordinate è chiamato asse x. L’asse verticale è chiamato asse Y. Il punto in cui i due assi si intersecano è chiamato origine. L’origine è a 0 sull’asse x e 0 sull’asse Y.
Gli assi x e y intersecanti dividono il piano delle coordinate in quattro sezioni. Queste quattro sezioni sono chiamate quadranti. I quadranti sono denominati usando i numeri romani I, II, III e IV che iniziano con il quadrante in alto a destra e si muovono in senso antiorario.
Le posizioni sul piano delle coordinate sono descritte come coppie ordinate. Una coppia ordinata indica la posizione di un punto mettendo in relazione la posizione del punto lungo l’asse x (il primo valore della coppia ordinata) e lungo l’asse y (il secondo valore della coppia ordinata).
In una coppia ordinata, come (x, y), il primo valore è chiamato coordinata x e il secondo valore è la coordinata y. Si noti che la coordinata x è elencata prima della coordinata y. Poiché l’origine ha una coordinata x di 0 e una coordinata y di 0, la sua coppia ordinata viene scritta (0, 0).
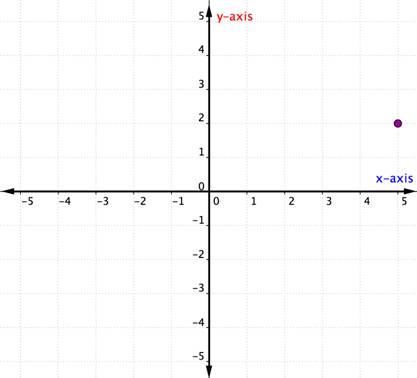
Considera il punto seguente.
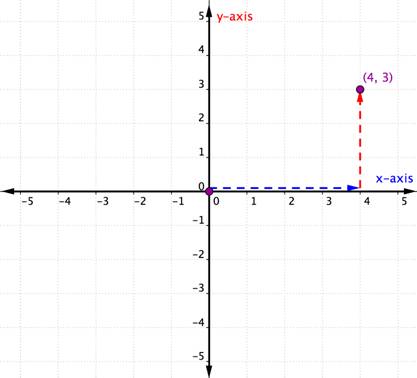
Per identificare la posizione di questo punto, iniziare dall’origine (0, 0) e spostarsi a destra lungo l’asse x fino a quando non si è sotto il punto. Guarda l’etichetta sull’asse X. Il 4 indica che, dall’origine, hai percorso quattro unità a destra lungo l’asse X. Questa è la coordinata x, il primo numero nella coppia ordinata.
Da 4 sull’asse x spostarsi fino al punto e notare il numero con cui si allinea sull’asse y. Il 3 indica che, dopo aver lasciato l’asse x, hai viaggiato 3 unità in direzione verticale, la direzione dell’asse y. Questo numero è la coordinata y, il secondo numero nella coppia ordinata. Con una coordinata x di 4 e una coordinata y di 3, hai la coppia ordinata (4, 3).
Diamo un’occhiata a un altro esempio.
|
Example |
||
|
Problem |
Describe the point shown as an ordered pair. |
|
|
|
||
|
(5, y) |
Inizia all’origine e si spostano lungo l’asse x. Questa è la coordinata x ed è scritta per prima nella coppia ordinata. |
|
|
(5, 2) |
Sposta da 5 a coppia ordinata e leggere il numero sull’asse y. Questa è la coordinata y ed è scritta seconda nella coppia ordinata. |
|
|
Risposta |
Il punto indicato come coppia ordinata è (5, 2). |
|
tracciamento di Punti nel Piano cartesiano
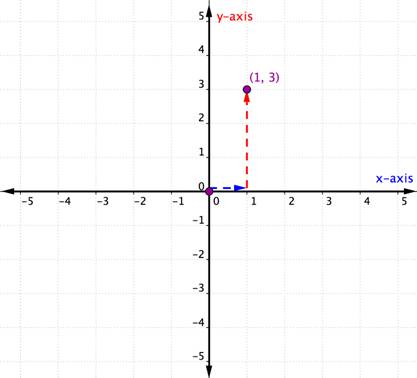
Ora che sapete come usare la x e y, è possibile tracciare una coppia ordinata pure. Basta ricordare, entrambi i processi iniziano all’origine – l’inizio! L’esempio che segue mostra come rappresentare graficamente la coppia ordinata (1, 3).
|
Example |
||
|
Problem |
Plot the point (1, 3). |
|
|
|
||
|
The x-coordinate is 1 because it comes first in the ordered pair. Inizia dall’origine e sposta una distanza di 1 unità in una direzione positiva (a destra) dall’origine lungo l’asse X. |
La coordinata y è 3 perché arriva seconda nella coppia ordinata. Da qui spostare direttamente 3 unità in una direzione positiva (up). Se guardi oltre all’asse y, dovresti essere allineato con 3 su quell’asse. |
|
|
Rispondi |
Disegna un punto in questa posizione ed etichetta il punto (1, 3). |
|
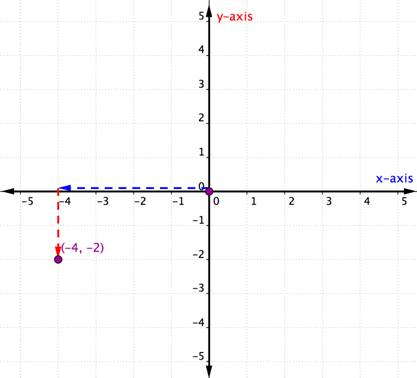
Nell’esempio precedente, entrambe le coordinate x e y erano positive. Quando una (o entrambe) delle coordinate di una coppia ordinata è negativa, sarà necessario spostarsi nella direzione negativa lungo uno o entrambi gli assi. Considera l’esempio seguente in cui entrambe le coordinate sono negative.
|
Example |
||
|
Problem |
Plot the point (−4, −2). |
|
|
|
||
|
The x-coordinate is −4 because it comes first in the ordered pair. Inizia dall’origine e sposta 4 unità in direzione negativa (a sinistra) lungo l’asse X. |
La coordinata y è -2 perché arriva seconda nella coppia ordinata. Ora sposta 2 unità in una direzione negativa (verso il basso). Se guardi oltre all’asse y, dovresti essere allineato con -2 su quell’asse. |
|
|
Rispondi |
Disegna un punto in questa posizione ed etichetta il punto (-4, -2). |
|
I passaggi per tracciare un punto sono riassunti di seguito.
Passi per tracciare una coppia ordinata (x, y) nel piano delle coordinate
o Determinare la coordinata x. Partendo dall’origine, sposta orizzontalmente, la direzione dell’asse x, la distanza data dalla coordinata x. Se la coordinata x è positiva, spostarsi a destra; se la coordinata x è negativa, spostarsi a sinistra.
o Determinare la coordinata y. A partire dalla coordinata x, spostare verticalmente, la direzione dell’asse y, la distanza data dalla coordinata y. Se la coordinata y è positiva, spostarsi verso l’alto; se la coordinata y è negativa, spostarsi verso il basso.
o Disegnare un punto nella posizione finale. Etichettare il punto con la coppia ordinata.
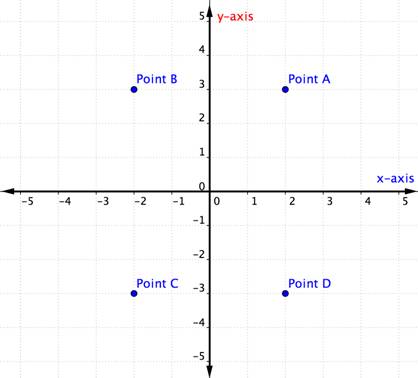
Quale punto rappresenta la coppia ordinata (-2, -3)?
Quattro Quadranti
Ordinato coppie all’interno di un particolare quadrante condividono determinate caratteristiche. Guarda ogni quadrante nel grafico qui sotto. Cosa noti dei segni delle coordinate x e y dei punti all’interno di ciascun quadrante?
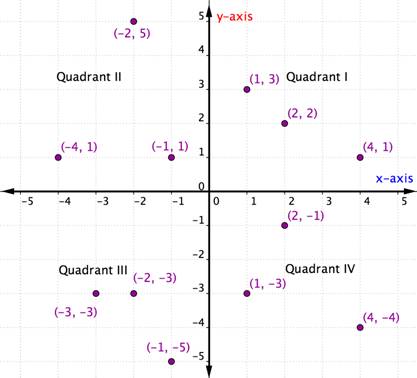
All’interno di ciascun quadrante, i segni delle coordinate x e delle coordinate y di ciascuna coppia ordinata sono gli stessi. Seguono anche uno schema, che è delineato nella tabella sottostante.
Una volta che si conoscono i quadranti nel piano delle coordinate, è possibile determinare il quadrante di una coppia ordinata senza nemmeno graficarlo guardando il grafico sopra. Ecco un altro modo di pensarci.
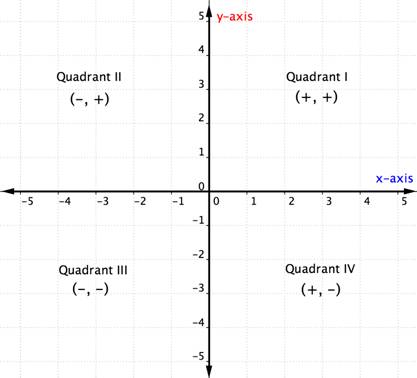
L’esempio seguente descrive come determinare la posizione del quadrante di un punto semplicemente pensando ai segni delle sue coordinate. Pensare alla posizione del quadrante prima di tracciare un punto può aiutarti a prevenire un errore. È anche una conoscenza utile per verificare di aver tracciato correttamente un punto.
Cosa succede se una coppia ordinata ha una coordinata x o y pari a zero? L’esempio seguente mostra il grafico della coppia ordinata (0, 4).
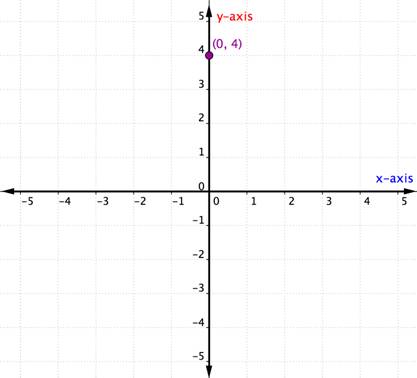
Un punto situato su uno degli assi non è considerato in un quadrante. È semplicemente su uno degli assi. Ogni volta che la coordinata x è 0, il punto si trova sull’asse y. Allo stesso modo, qualsiasi punto che ha una coordinata y pari a 0 si troverà sull’asse X.
Quale delle descrizioni seguenti descrive meglio la posizione del punto (8, 0)?
A) Quadrante I
B) è sull’asse x
C) è sull’asse y
D) Coordinate aereo
Sintesi
piano cartesiano è un sistema per la rappresentazione grafica e descrizione di punti e linee. Il piano delle coordinate è composto da un asse orizzontale (x-) e un asse verticale (y -). L’intersezione di queste linee crea l’origine, che è il punto (0, 0). Il piano delle coordinate è diviso in quattro quadranti. Insieme, queste caratteristiche del sistema di coordinate consentono la rappresentazione grafica e la comunicazione su punti, linee e altri concetti algebrici.