Purplemath
In matematica, una “identità” è un’equazione che è sempre vera. Questi possono essere” banalmente ” veri, come “x = x” o utilmente veri, come il Teorema di Pitagora “a2 + b2 = c2” per i triangoli rettangoli. Ci sono un sacco di identità trigonometriche, ma le seguenti sono quelle che è più probabile vedere e utilizzare.
Basic & Pythagorean, Angle-Sum & -Difference, Double-Angle, Half-Angle, Sum, Product
Content Continues Below
MathHelp.com
Need a custom math course?
K12 | College | Test Prep

di Base e di Pitagora Identità
Affiliato
da Notare come un “co-(qualcosa)”trig rapporto è sempre il reciproco di alcuni “non-co” rapporto. Puoi usare questo fatto per aiutarti a mantenere dritto che la cosecante va con il seno e la secante va con il coseno.
Le seguenti (in particolare la prima delle tre sotto) sono chiamate identità “pitagoree”.
sin2(t) + cos2(t) = 1
tan2(t) + 1 = sec2(t)
1 + cot2(t) = csc2(t)
Pubblicità
si noti che i tre identità coinvolgere soprattutto la quadratura e il numero 1. Puoi vedere chiaramente la relazione Pitagorica-la relazione se consideri il cerchio unitario, dove l’angolo è t, il lato “opposto” è sin(t) = y, il lato “adiacente” è cos(t) = x e l’ipotenusa è 1.
Abbiamo identità aggiuntive relative al lo stato funzionale del trig rapporti:
sin(–t) = –sin(t)
cos(–t) = cos(t)
tan(–t) = –tan(t)
si Noti in particolare che il seno e tangente sono dispari funzioni, essendo simmetrica rispetto all’origine, mentre il coseno è anche la funzione, essendo simmetrica intorno all’asse y. Il fatto che si possa prendere il segno “meno” dell’argomento all’esterno (per seno e tangente) o eliminarlo completamente (per coseno) può essere utile quando si lavora con espressioni complicate.
Angolo di-Somma e Differenza di Identità
sin(α + β) = sin(α) cos(β) + cos(α) sin(β)
sin(α – β) = sin(α) cos(β) – cos(α) sin(β)
cos(α + β) = cos(α) cos(β) – sin(α) sin(β)
cos(α – β) = cos(α) cos(β) + sin(α) sin(β)
il modo in cui sopra identità, gli angoli sono indicati con lettere greche. La lettera di tipo a, “α”, è chiamata” alfa”, che si pronuncia”AL-fuh”. La lettera di tipo b, “β”, è chiamata” beta”, che si pronuncia”BAY-tuh”.
Contenuto Continua qui Sotto
Doppio-Angolo di Identità
sin(2x) = 2 sin(x) cos(x)
cos(2x) = cos2(x) – sin2(x) = 1 – 2 sin2(x) = 2 cos2(x) – 1
Mezzo Angolo di Identità
L’identità può essere ri-affermato dalla quadratura ogni lato e il raddoppio di tutte le angolo di misure. I risultati sono i seguenti:
Affiliate

Sum Identities
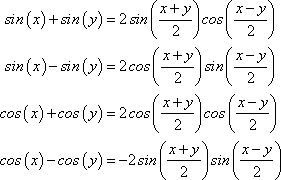
Product Identities
Affiliato
Si prevede di utilizzare tutte queste identità, o quasi, per l’accertamento di altri trig identità e per la risoluzione di equazioni trigonometriche. Tuttavia, se hai intenzione di studiare il calcolo, presta particolare attenzione alle identità di semiangolo seno e coseno, perché le userai molto nel calcolo integrale.
URL: https://www.purplemath.com/modules/idents.htm