Dopo aver compreso la funzione esponenziale, il nostro prossimo obiettivo è il logaritmo naturale.
Dato come il log naturale è descritto nei libri di matematica, c’è poco “naturale” a riguardo: è definito come l’inverso di^e ^ x already, un esponente abbastanza strano già.
Ma c’è una spiegazione fresca e intuitiva: il registro naturale ti dà il tempo necessario per raggiungere un certo livello di crescita.
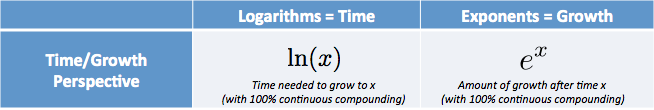
Supponiamo di avere un investimento in orsetti gommosi (chi non lo fa?) con un tasso di interesse del 100% all’anno, in continua crescita. Se vuoi una crescita di 10 volte, assumendo un compounding continuo, aspetteresti solo \ \ ln (10) or o 2.302 anni. Non capisco perché ci vogliono solo pochi anni per ottenere una crescita di 10 volte? Non vedo perché il modello non è 1, 2, 4, 8? Leggi di più su e.
e e il Log naturale sono gemelli:
- $e^x is è l’importo che abbiamo dopo aver iniziato a 1.0 e in continua crescita per $x$ unità di tempo
- $\ln(x)$ (Logaritmo Naturale) è il tempo per raggiungere l’importo di $x$, supponendo che siamo cresciuti costantemente dal 1.0
Non male, vero? Mentre i matematici si arrampicano per darti la lunga spiegazione tecnica, tuffiamoci in quella intuitiva.
E riguarda la crescita
Il numero e riguarda la crescita continua. Come abbiamo visto l’ultima volta, $e^x us ci consente di unire tasso e tempo: 3 anni con una crescita del 100% è lo stesso di 1 anno con una crescita del 300%, quando continuamente aggravata.
Possiamo prendere qualsiasi combinazione di tasso e tempo (50% per 4 anni) e convertire il tasso al 100% per comodità (dandoci il 100% per 2 anni). Con la conversione a un tasso del 100%, dobbiamo solo pensare al tempo che componente:
![]()
Intuitivamente, $e^x$ significa:
- la crescita ottengo dopo x unità di tempo (e il 100% continua crescita)
- Per esempio: dopo 3 periodi di tempo ho $e^3$ = 20.08 volte la quantità di “roba”.
$e^x is è un fattore di scala, che ci mostra quanta crescita otterremmo dopo units x units unità di tempo.
Il log naturale è sul tempo
Il log naturale è l’inverso di^e ^ x^, un termine di fantasia per opposto. Parlando di fantasia, il nome latino è logarithmus naturali, dando l’abbreviazione ln.
Ora cosa significa questa roba inversa o opposta?
- – e ^ x-ci permette di collegare in tempo e ottenere la crescita.
- \ \ ln (x) lets ci consente di collegare la crescita e ottenere il tempo necessario.
Per esempio:
- $e^3 is è 20.08. Dopo 3 unità di tempo, finiamo con 20.08 volte quello che abbiamo iniziato con.
- $\ln (20.08) is è di circa 3. Se vogliamo una crescita di 20.08, aspetteremmo 3 unità di tempo (di nuovo, assumendo un tasso di crescita continuo del 100%).
Con me? Il registro naturale ci dà il tempo necessario per colpire la nostra crescita desiderata.
L’aritmetica logaritmica non è normale
Hai studiato i registri prima, ed erano strane bestie. Come hanno trasformato la moltiplicazione in aggiunta? Divisione in sottrazione? Vediamo.
Che cos’è \ \ ln (1)$? Intuitivamente, la domanda è: quanto tempo devo aspettare per ottenere 1x il mio importo attuale?
Zero. Zip. Niente. Sei già a 1x il tuo importo attuale! Non ci vuole tempo per crescere da 1 a 1.
- Ok\ln(1) = 0 Ok
Ok, che ne dici di un valore frazionario? Quanto tempo per ottenere 1/2 il mio importo attuale? Supponendo che tu stia crescendo continuamente al 100%, sappiamo che $\ln(2) is è la quantità di tempo da raddoppiare. Se lo invertiamo (cioè prendiamo il tempo negativo) avremmo metà del nostro valore corrente.
- \ \ ln(.5) = – \ ln(2)= -.693 Makes
Ha senso, giusto? Se torniamo indietro .693 unità (secondi negativi, diciamo) avremmo metà del nostro importo attuale. In generale, puoi capovolgere la frazione e prendere il negativo: \ \ ln(1/3) = – \ln (3) = -1.09$. Questo significa che se torniamo indietro di 1,09 unità di tempo, avremo un terzo di quello che abbiamo ora.
Ok, che ne dici del registro naturale di un numero negativo? Quanto tempo ci vuole per “far crescere” la tua colonia di batteri da 1 a -3?
È impossibile! Non puoi avere una quantità” negativa ” di batteri, vero? Al massimo (ehm least almeno) puoi avere zero, ma non c’è modo di avere una quantità negativa delle piccole creature. I batteri negativi non hanno senso.
- $\ln(\text{negative number}) = \text{undefined}
Undefined significa solo “non c’è tempo che puoi aspettare” per ottenere un importo negativo. (Beh, se usiamo esponenziali immaginari, c’è una soluzione. Ma oggi manteniamo la realtà.)
La moltiplicazione logaritmica è molto divertente
Quanto tempo ci vuole per far crescere 9 volte il tuo importo attuale? Certo, potremmo usare ln (9). Ma è troppo facile, siamo diversi.
Possiamo considerare la crescita 9x come triplicare (prendendo units \ ln(3) units unità di tempo) e poi triplicare di nuovo (prendendo un’altra units \ ln(3) units unità di tempo):
- Tempo di crescere 9x = \\ln(9) = = Tempo di triplicare e triplicare di nuovo = \ \ ln(3) + \ ln(3) Interesting
Interessante. Qualsiasi numero di crescita, come 20, può essere considerato crescita 2x seguita da crescita 10x. O crescita 4x seguita da crescita 5x. O 3x crescita seguita da 6.666 x crescita. Vedi lo schema?
- $\ln(a*b) = \ln(a) + \ln(b)
Il log di a per b = log(a) + log(b). Questa relazione ha senso quando si pensa in termini di tempo per crescere.
Se vogliamo crescere 30x, ci si può aspettare $\ln(30)$ tutti in una volta, o semplicemente aspettare $\ln(3)$, da tripla, quindi attendere che $\ln(10)$, per crescere 10x di nuovo. L’effetto netto è lo stesso, quindi anche il tempo netto dovrebbe essere lo stesso (ed è).
Che ne dici della divisione? $ \ ln (5/3) means significa: Quanto tempo ci vuole per crescere 5 volte e poi prendere 1/3 di quello?
Bene, crescere 5 volte è is \ ln(5)$. La crescita di 1/3 è units – \ ln(3) units unità di tempo. Quindi
- \\ln(5/3) = \ln(5) – \ ln(3) Which
Che dice: Crescere 5 volte e “tornare indietro nel tempo” fino a quando non hai un terzo di tale importo, quindi ti rimane una crescita di 5/3. In generale abbiamo
- \\ln(a/b) = \ln(a) – \ ln(b)
Spero che la strana matematica dei logaritmi stia iniziando ad avere senso: la moltiplicazione della crescita diventa addizione del tempo, la divisione della crescita diventa sottrazione del tempo. Non memorizzare le regole, capirle.
Usando log naturali con qualsiasi tasso
“Certo”, dici, ” Questa roba di log funziona per una crescita del 100%, ma per quanto riguarda il 5% che normalmente ottengo?”
Non è un problema. Il ” tempo “che otteniamo da $\ln () actually è in realtà una combinazione di velocità e tempo, la” x” dalla nostra equazione^e ^ x.. Assumiamo solo il 100% per renderlo semplice, ma possiamo usare altri numeri.
Supponiamo di volere una crescita 30x: plug in \ \ ln (30) get e ottieni 3.4. Questo significa:
- $e^x = \text{growth}
- ^e ^ {3.4} = 30
E intuitivamente questa equazione significa “il rendimento del 100% per 3,4 anni è una crescita 30x”. Possiamo considerare l’equazione:
![]()
![]()
E ‘ possibile modificare il “tasso” e “il tempo”, fintanto che il tasso di * tempo = 3.4. Ad esempio, supponiamo di volere una crescita 30x – quanto tempo aspettiamo assumendo un rendimento del 5%?
- $\ln(30) = 3.4
- \\text{rate} * \ text{time} = 3.4
- $.05 * \ text{time} = 3.4
- \ \ text{time} = 3.4/.05 = 68 \text{years}
Intuitivamente, penso “\ \ ln(30) = 3.4$, quindi con una crescita del 100% ci vorranno 3.4 anni. Se raddoppio il tasso di crescita, dimezzo il tempo necessario.”
- 100% per 3,4 anni = 1,0 * 3,4 = 3,4
- 200% per 1,7 anni = 2,0 * 1,7 = 3,4
- 50% per 6,8 anni = 0,5 * 6,8 = 3,4
- 5% per 68 anni = .05 * 68 = 3.4
Bello, eh? Il registro naturale può essere utilizzato con qualsiasi tasso di interesse o di tempo fino a quando il loro prodotto è lo stesso. Puoi muovere le variabili quanto vuoi.
Esempio impressionante: La regola del 72
La regola del 72 è una scorciatoia matematica mentale per stimare il tempo necessario per raddoppiare i vostri soldi. Stiamo andando a derivarlo (yay!) e ancora meglio, lo capiremo intuitivamente.
Quanto tempo ci vuole per raddoppiare i tuoi soldi con un interesse del 100%, aggravato ogni anno?
Uh oh. Abbiamo usato il registro naturale per le tariffe continue, ma ora stai chiedendo interessi annuali? Non rovinera ‘ la nostra formula? Sì, lo farà, ma a tassi di interesse ragionevoli come il 5%, il 6% o anche il 15%, non c’è molta differenza tra l’interesse annuale composto e completamente continuo. Quindi la formula approssimativa funziona, uh, approssimativamente e fingeremo di avere un interesse completamente continuo.
Ora la domanda è facile: per quanto tempo raddoppiare al 100% di interesse? ln(2) = .693. Ci vuole .693 unità di tempo (anni, in questo caso) per raddoppiare i vostri soldi con compounding continuo con un tasso del 100%.
Ok, cosa succede se il nostro interesse non è al 100% Cosa succede se è 5% o 10%?
Semplice. Fino a quando tasso * tempo = .693, raddoppieremo i nostri soldi:
- rate * time = .693
- tempo = .693 / rate
Quindi, se avessimo solo una crescita del 10%, ci vorrebbe .693 / .10 o 6,93 anni per raddoppiare.
Per semplificare le cose, moltiplichiamo per 100 in modo da poter parlare di 10 piuttosto che .10:
- tempo di raddoppiare = 69,3 / tasso, dove si presume che il tasso sia in percentuale.
Ora il tempo di raddoppiare con una crescita del 5% è di 69,3 / 5 o 13,86 anni. Tuttavia, 69.3 non è il numero più divisibile. Scegliamo un vicino vicino, 72, che può essere diviso per 2, 3, 4, 6, 8 e molti altri numeri.
- tempo di raddoppiare = 72/rate
che è la regola di 72! Facile ventilato.
Se vuoi trovare il tempo per triplicare, useresti ln(3) ~ 109.8 e ottieni
- time to triple = 110 / rate
Che è un’altra utile regola empirica. La regola del 72 è utile per i tassi di interesse, la crescita della popolazione, colture di batteri, e tutto ciò che cresce in modo esponenziale.
Dove da qui?
Spero che il registro naturale abbia più senso — ti dice il tempo necessario per qualsiasi quantità di crescita esponenziale. Lo considero ” naturale “perché e è il tasso universale di crescita, quindi ln potrebbe essere considerato il modo” universale” per capire quanto tempo ci vuole per crescere.
Quando vedi $ \ ln(x) think, pensa solo “la quantità di tempo per crescere fino a x”. Nel prossimo articolo porteremo e e ln insieme, e il dolce aroma della matematica riempirà l’aria.
Appendice: Il registro naturale di E
Quiz rapido: cosa c’è $ \ ln (e)$?
- Il robot matematico dice: Poiché sono definiti come funzioni inverse, chiaramente clearly\ln(e) = 1 The
- L’umano intuitivo: ln (e) è la quantità di tempo necessaria per ottenere unità di crescita “e” (circa 2.718). Ma e è la quantità di crescita dopo 1 unità di tempo, quindi \ \ ln(e) = 1$.
Pensa in modo intuitivo.
Altri Post In Questa Serie
- Una Guida Intuitiva Per Funzioni Esponenziali & e
- Demistificare il Logaritmo Naturale (ln)
- Una Guida Visiva per Semplice, Composto e Continuo Tassi di Interesse
- Definizioni Comuni e (Colorato)
- la Comprensione Esponenti (Perché 0^0 = 1?)
- Usare i logaritmi nel mondo reale
- Come pensare con esponenti e logaritmi
- Capire la crescita discreta rispetto a quella continua
- Cosa significa veramente un esponente?
- Q: Perché è e speciale? (2.718…, non 2, 3.7 o un altro numero?)