In altre sezioni è stato detto che molte delle proprietà di solidi, liquidi e gas potrebbero essere valutate, se si assume che le sostanze sono fatte di atomi o molecole che sono costantemente in movimento. La legge di Boyle e le altre leggi sui gas ci hanno dato molte più informazioni quantitative sui gas, e vale la pena chiedersi se con il modello precedente possiamo fare previsioni quantitative in accordo con queste leggi. Rispondendo a questa domanda, acquisiremo anche importanti informazioni sulla natura della temperatura e dell’energia termica.

La teoria microscopica del comportamento dei gas basata sul movimento molecolare è chiamata teoria cinetica dei gas. I suoi postulati di base sono elencati nella Tabella 1:

TABLE \(\PageIndex{1}\) Postulati della Teoria cinetica dei gas.

1 Le molecole di un gas sono piccole e molto distanti tra loro. La maggior parte del volume che un gas occupa è spazio vuoto.

2 molecole di gas sono in costante movimento casuale. Proprio come molte molecole si muovono in una direzione come in qualsiasi altra.

3 molecole possono scontrarsi tra loro e con le pareti del contenitore. Le collisioni con le pareti rappresentano la pressione del gas.

4 Quando si verificano collisioni, le molecole non perdono energia cinetica; cioè, si dice che le collisioni siano perfettamente elastiche. L’energia cinetica totale di tutte le molecole rimane costante a meno che non ci sia qualche interferenza esterna con

5 Le molecole non esercitano forze attraenti o repulsive l’una sull’altra tranne durante il processo di collisione. Tra le collisioni, si muovono in linee rette.

Da essi è possibile ricavare la seguente espressione per la pressione di un gas in termini di proprietà di molecole:

\ (P, V = pressione e volume del gas

N = numero di molecole

m = massa di ogni molecola

(u2)ave = media (o medio) dei quadrati di tutti i singoli molecolare velocità. Questa velocità quadrata media deve essere utilizzata perché la pressione è proporzionale al quadrato della velocità molecolare e le collisioni molecolari causano diverse molecole ad avere velocità molto diverse.

Piuttosto che preoccuparci della procedura per la derivazione dell’Eq. \(\ref{1}\), esaminiamo l’equazione e vediamo che le sue caratteristiche generali sono molto simili a quelle che ci aspetteremmo. In qualche modo, la capacità di farlo con una formula è più utile della capacità di derivarla. Figura \ (\PageIndex{1}\)

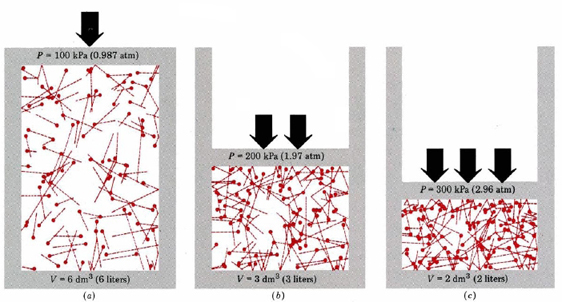Prima di tutto, l’equazione ci dice che la pressione di un gas è proporzionale al numero di molecole diviso per il volume. Questo è mostrato graficamente nella figura \ (\PageIndex{1}\), dove un computer ha disegnato lo stesso numero di molecole di gas che occupano ciascuno dei tre volumi diversi. La “coda” su ogni molecola mostra il percorso esatto seguito da quella molecola nel microsecondo precedente—più lunga è la coda, più velocemente la molecola stava andando. La media dei quadrati delle lunghezze della coda è proporzionale a (u2)ave ed è la stessa in tutti e tre i diagrammi. Si presume anche che tutte le molecole abbiano masse uguali.

Come si può vedere, riducendo il volume del gas aumenta il numero di collisioni per unità di superficie sulle pareti del contenitore. Ogni collisione esercita forza sulla parete; la forza per unità di area è pressione, e quindi il numero di collisioni per unità di area è proporzionale alla pressione. Dimezzare il volume raddoppia la pressione, una previsione che concorda con i fatti sperimentali riassunti nella legge di Boyle. Equazione \(\ref {1}\) dice anche che la pressione è proporzionale alla massa di ogni molecola di gas. Ancora una volta, questo è quello che ci aspetteremmo. Le molecole pesanti danno una “spinta”più grande(il termine tecnico per questo è impulso) contro il muro rispetto a quelle leggere con la stessa velocità.

Infine, l’equazione ci dice che la pressione è proporzionale alla media dei quadrati delle velocità molecolari. Questa dipendenza dal quadrato della velocità è ragionevole se ci rendiamo conto che raddoppiare la velocità di una molecola ha due effetti.

In primo luogo, la molecola può muoversi più lontano in un dato periodo di tempo, raddoppiando il numero di collisioni con le pareti. Questo raddoppierebbe la pressione. In secondo luogo, raddoppiando la velocità di una molecola raddoppia la spinta o l’impulso di ogni collisione. Questo raddoppia di nuovo la pressione. Quindi raddoppiare la velocità di una molecola quadruplica la pressione, e per un gran numero di molecole, P è proporzionale alla velocità quadrata media.