Orbitali atomici
Un orbitale è il perfezionamento quantomeccanico dell’orbita di Bohr. In contrasto con il suo concetto di una semplice orbita circolare con un raggio fisso, gli orbitali sono regioni matematicamente derivate dello spazio con diverse probabilità di avere un elettrone.
Un modo di rappresentare le distribuzioni di probabilità degli elettroni è stato illustrato nella Figura 6.5.2 per l’orbitale 1s dell’idrogeno. Poiché Ψ2 dà la probabilità di trovare un elettrone in un dato volume di spazio (come un picometro cubico), un grafico di Ψ2 rispetto alla distanza dal nucleo (r) è un grafico della densità di probabilità. L’orbitale 1s è sfericamente simmetrico, quindi la probabilità di trovare un elettrone 1s in un dato punto dipende solo dalla sua distanza dal nucleo. La densità di probabilità è maggiore a r = 0 (al nucleo) e diminuisce costantemente con l’aumentare della distanza. A valori molto grandi di r, la densità di probabilità dell’elettrone è molto piccola ma non zero.
Al contrario, possiamo calcolare la probabilità radiale (la probabilità di trovare un elettrone 1s ad una distanza r dal nucleo) sommando le probabilità di un elettrone che si trova in tutti i punti su una serie di gusci sferici x di raggio r1, r2, r3,…, rx − 1, rx. In effetti, stiamo dividendo l’atomo in gusci concentrici molto sottili, proprio come gli strati di una cipolla (parte (a) in Figura \(\PageIndex{1}\)), e calcolando la probabilità di trovare un elettrone su ogni guscio sferico. Ricordiamo che la densità di probabilità degli elettroni è maggiore a r = 0 (parte (b) in Figura \(\PageIndex{1}\)), quindi la densità dei punti è maggiore per i gusci sferici più piccoli in parte (a) in Figura \(\PageIndex{1}\). Al contrario, la superficie di ciascun guscio sferico è uguale a 4nr2, che aumenta molto rapidamente con l’aumentare di r (parte (c) in Figura \(\PageIndex{1}\)). Poiché l’area superficiale dei gusci sferici aumenta più rapidamente con l’aumentare di r rispetto alla diminuzione della densità di probabilità degli elettroni, il grafico della probabilità radiale ha un massimo a una particolare distanza (parte (d) in Figura \(\PageIndex{1}\)). Più importante, quando r è molto piccola, la superficie di un guscio sferico è così piccola che la probabilità totale di trovare un elettrone vicino al nucleo è molto bassa; al nucleo, la probabilità dell’elettrone svanisce (parte (d) in Figura \(\PageIndex{1}\)).

Per l’atomo di idrogeno, il picco nel diagramma di probabilità radiale si verifica a r = 0,529 Å (52,9 pm), che è esattamente il raggio calcolato da Bohr per l’orbita n = 1. Quindi il raggio più probabile ottenuto dalla meccanica quantistica è identico al raggio calcolato dalla meccanica classica. Nel modello di Bohr, tuttavia, l’elettrone è stato assunto per essere a questa distanza 100% del tempo, mentre nel modello di Schrödinger meccanica quantistica, è a questa distanza solo una parte del tempo. La differenza tra i due modelli è attribuibile al comportamento ondulatorio dell’elettrone e al principio di indeterminazione di Heisenberg.
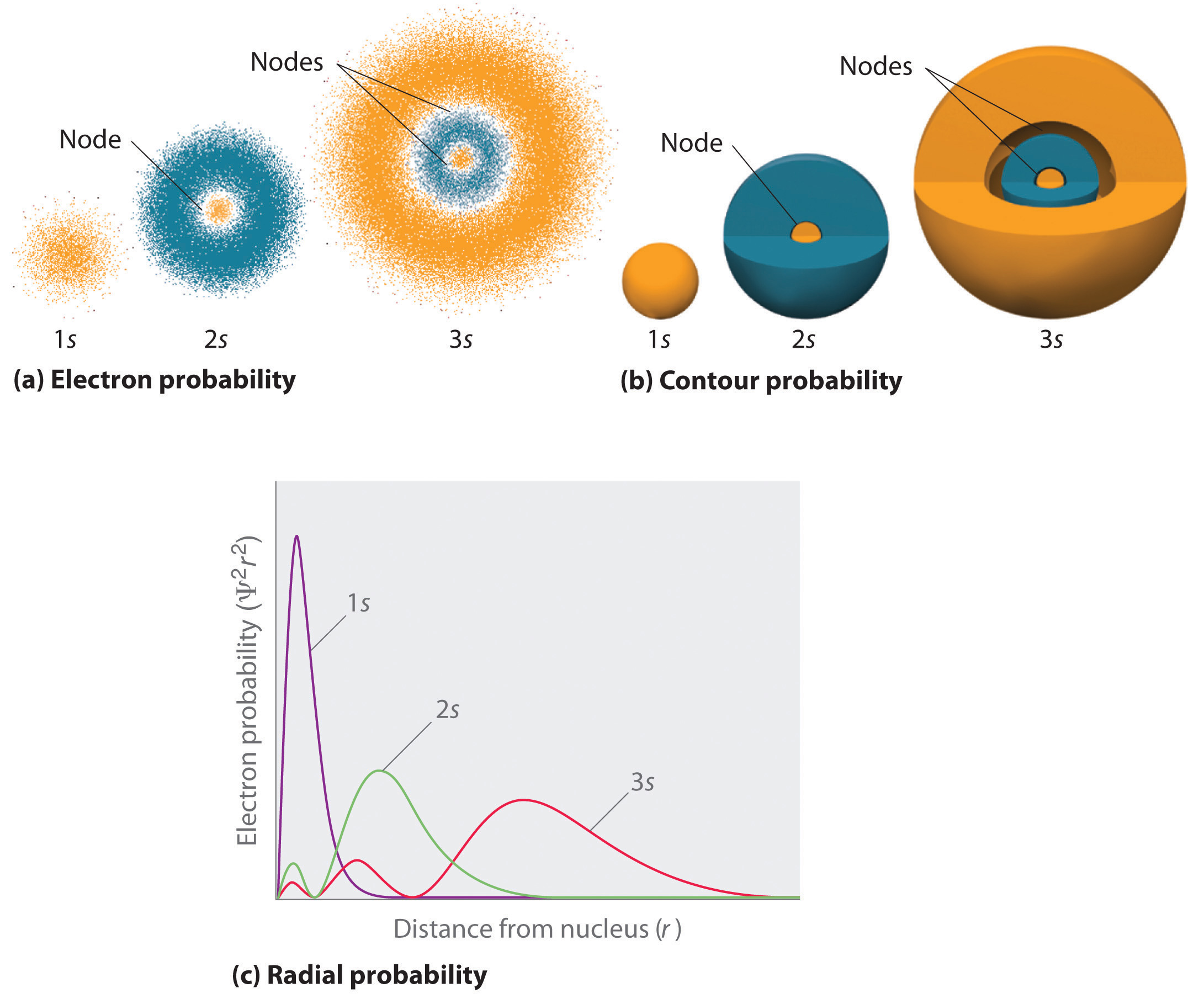
Figura \ (\PageIndex{2}\) confronta le densità di probabilità degli elettroni per gli orbitali idrogeno 1s, 2s e 3s. Si noti che tutti e tre sono sfericamente simmetrici. Per gli orbitali 2s e 3s, tuttavia (e anche per tutti gli altri orbitali s), la densità di probabilità degli elettroni non cade senza problemi con l’aumentare di r. Invece, una serie di minimi e massimi sono osservati nei grafici di probabilità radiale (parte (c) in Figura \(\PageIndex{2}\)). I minimi corrispondono a nodi sferici (regioni di probabilità di elettroni zero), che si alternano a regioni sferiche di probabilità di elettroni diversi da zero.