joitakin mielenkiintoisia asioita kulmista ja ympyröistä.
- kaiverrettu kulma
- kaiverretut Kulmalauseet
- esimerkki: mikä on koko kulma POQ? (O on ympyrän keskipiste)
- esimerkki: mikä on kulman CBX koko?
- kulma puoliympyrässä (Thalesin lause)
- toinen good reason why it works
- esimerkki: mikä on kulman BAC koko?
- ympyrän keskipisteen löytäminen
- syklinen nelikulmio
- esimerkki: mikä on kulman WXY koko?
kaiverrettu kulma
ensinnäkin määritelmä:
kaiverrettu kulma: kulma, joka on tehty ympyrän kehällä istuvista pisteistä.
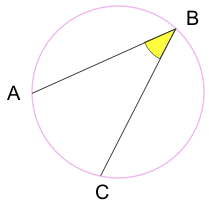
a ja C ovat ”päätepisteitä”
b on ”kärkipiste”
pelaa sen kanssa tästä:
kun siirrät pistettä ”B”, mitä tapahtuu kulmalle?
kaiverretut Kulmalauseet
kaiverrettu kulma A° on puolet keskuskulmasta 2A°
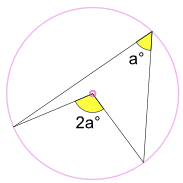
(kutsutaan kulmaa keskipisteessä lause)
ja (pitää päätepisteet kiinteinä) …
… kulma A° on aina sama,
riippumatta siitä, missä se on samalla kaarella päätepisteiden välillä:
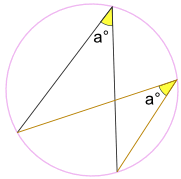
kulma A° on sama.
(kutsutaan kulmat Subtended saman Kaarilause)
esimerkki: mikä on koko kulma POQ? (O on ympyrän keskipiste)
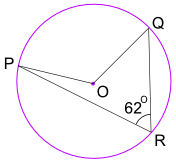
kulma POQ = 2 × kulma PRQ = 2 × 62° = 124°
esimerkki: mikä on kulman CBX koko?
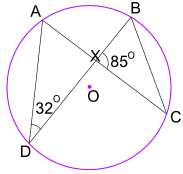
kulma ADB = 32° on myös kulma ACB.
ja kulma ACB vastaa myös kulmaa XCB.
joten kolmiossa BXC tiedämme kulman BXC = 85°, ja kulmassa XCB = 32°
nyt käytetään kolmion kulmia lisätään 180° :
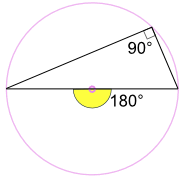
kulma puoliympyrässä (Thalesin lause)
kulma ympyrän halkaisijan poikki on aina oikeassa kulmassa:
(päätepisteet ovat ympyrän halkaisijan kumpaakin päätä,
kärkipiste voi olla missä tahansa ympärysmitta.)
|
miksi? Koska: kaiverrettu kulma 90° on puolet keskuskulmasta 180° (käyttäen ”kulmaa keskipisteessä lause” edellä) |
 |
toinen good reason why it works
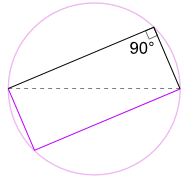
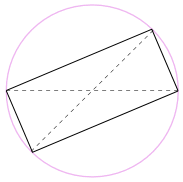
voisimme myös kiertää muotoa 180° tehdä suorakulmion!
se on suorakulmio, koska kaikki sivut ovat yhdensuuntaiset ja molemmat lävistäjät ovat yhtä suuret.
, joten sen sisäkulmat ovat kaikki Suorakulmaisia (90°).
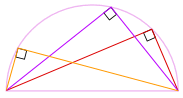
niin siinä mennään! Riippumatta siitä, missä kulma on
kehällä, se on aina 90°
esimerkki: mikä on kulman BAC koko?
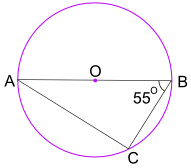
puoliympyrän lauseen kulma kertoo, että kulma ACB = 90°
Käytä nyt kolmion kulmia lisää 180° löytääksesi kulman BAC:
ympyrän keskipisteen löytäminen
Voimme käyttää tätä ajatusta ympyrän keskipisteen löytämiseen:
- piirtää suoran kulman mistä tahansa ympyrän kehällä, piirrä sitten halkaisija, jossa kaksi jalkaa osuvat ympyrään
- tee se uudelleen, mutta eri halkaisijalle
, jossa halkaisijat risteytyvät keskipisteenä!
syklinen nelikulmio
|
”syklisessä” Nelikulmiossa on jokainen verteksi ympyrän kehällä: |
 |
p>syklisen nelikulmion vastakkaiset kulmat lisäävät 180°:
|
 |
esimerkki: mikä on kulman WXY koko?
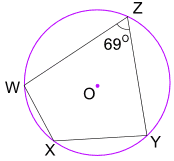
Opposite angles of a cyclic quadrilateral add to 180°

